
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пунтк 4. Алгебраические дополнения и миноры.Содержание книги
Поиск на нашем сайте
Пусть имеем определитель третьего порядка: Минором, соответствующим данному элементу aij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i -ой строки и j -го столбца. Миноры соответствующие данному элементу aij будем обозначать Mij. Например, минором M12, соответствующим элементу a12, будет определитель Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a12, берётся со знаком “–”, т.е. можно записать, что
Алгебраическим дополнением элемента aij определителя называется его минор Mij, умноженный на (–1)i+j. Алгебраическое дополнение элемента aij обозначается Aij. Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством Aij = (–1)i+j Mij. Например, Пример 7. Дан определитель
Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде:
Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца. Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем:
Разложим полученный определитель по элементам 1-ой строки.
Отсюда Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов. Таким образом, справедлива следующая теорема. Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения. Всё вышесказанное справедливо и для определителей любого более высокого порядка. Пример 8. 1. Вычислить определитель
2. Вычислить определитель, используя его свойства. Прежде чем раскладывать определитель по элементам какой–либо строки, сводя к определителям третьего порядка, преобразуем его, используя свойство 7, сделав в какой–либо строке или столбце все элементы, кроме одного, равными нулю. В данном случае удобно рассмотреть 4-й столбец или 4-ю строку:
Пункт 5. Обратная матрица. Понятие обратной матрицы вводится только для квадратных матриц. Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A-1 и удовлетворяющая условию Справедлива следующая теорема: Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля. Если условия теоремы выполнены, то матрица обратная к матрице
где Aij - алгебраические дополнения элементов aij данной матрицы A. Итак, чтобы найти обратную матрицу нужно: 1. Найти определитель матрицы A. 2. Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу 3. Найти матрицу, транспонированную полученной матрице Аналогично для матриц второго порядка, обратной будет следующая матрица Пример 9. 1. Найти матрицу, обратную данной | A | = 2. Найдем алгебраические дополнения элементов матрицы A.
Проверка:
Аналогично A∙A-1 = E. 2. Найти элементы
Вычислим | A | = 4. Тогда
3.
Тема 1.2. Системы линейных уравнений. Понятие систем линейных уравнений и методы их решения. Матричный метод. Правило Крамера. Метод Гаусса.
|
||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |

 .
. , который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.
, который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца. .
.

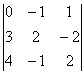 . Найти A13, A21, A32.
. Найти A13, A21, A32.
 .
.
 .
.
 т.к. определители второго порядка в формуле (2) есть миноры элементов a21, a22, a23. Таким образом,
т.к. определители второго порядка в формуле (2) есть миноры элементов a21, a22, a23. Таким образом, 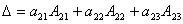 , т.е. мы получили разложение определителя по элементам 2-ой строки.
, т.е. мы получили разложение определителя по элементам 2-ой строки. , раскладывая его по элементам 2-го столбца.
, раскладывая его по элементам 2-го столбца.
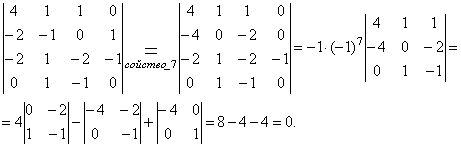
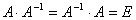 , где Е – единичная матрица.
, где Е – единичная матрица. находится следующим образом
находится следующим образом ,
, , элементами которой являются числа Aij.
, элементами которой являются числа Aij. – это и будет
– это и будет  .
. .
. . Сделать проверку.
. Сделать проверку.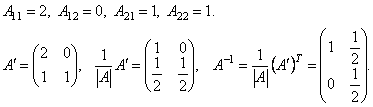
 .
. и
и  матрицы A-1 обратной данной
матрицы A-1 обратной данной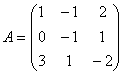 .
. .
.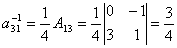 .
. . Найдем обратную матрицу.
. Найдем обратную матрицу.



