Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 1. Основы линейной алгебры.Содержание книги Поиск на нашем сайте
МОДУЛЬ 1. ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ. Тема 1.1. Матрицы и действия с ними. Определение и виды матриц. Действия с матрицами. Определитель и его свойства. Алгебраические дополнения и миноры. Обратная матрица. Пункт 1. Определение и виды матриц. Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В. В общем виде матрицу размером m × n записывают так
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце. Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1. Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья. Различаются также матрицы, имеющие только одну строку или один столбец. Матрица, у которой всего одна строка Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,
Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.
Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.
Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид Пункт 2. Действия с матрицами. Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны aij = bij. Так если Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием. Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT. Связь между матрицей A и её транспонированной можно записать в виде Пример 1. Найти матрицу транспонированную данной. 1. 2. Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,
Или Пример 2. Найти сумму матриц: 1. 2. 3. Сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+ C = A +(B+C). Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу Для любых чисел a и b и матриц A и B выполняются равенства: 1. 2. 3. Пример 3. 1. 2. Найти 2A-B, если
3. Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры. Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:
Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы. В общем случае, если мы умножаем матрицу A = (aij) размера m × n на матрицу B = (bij) размера n × p, то получим матрицу C размера m × p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i -ой строки матрицы A на соответствующие элементы j -го столбца матрицы B и их сложения. Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат. Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,
Пример 4. 1. Пусть Найти элементы c12, c23 и c21 матрицы C.
2. Найти произведение матриц.
3. 4. 5. Пусть Найти АВ и ВА.
6. Найти АВ и ВА.
Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей. Умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC. При умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A. Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице. Например, если
Пример 8. 1. Вычислить определитель
2. Вычислить определитель, используя его свойства. Прежде чем раскладывать определитель по элементам какой–либо строки, сводя к определителям третьего порядка, преобразуем его, используя свойство 7, сделав в какой–либо строке или столбце все элементы, кроме одного, равными нулю. В данном случае удобно рассмотреть 4-й столбец или 4-ю строку:
Пункт 5. Обратная матрица. Понятие обратной матрицы вводится только для квадратных матриц. Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A-1 и удовлетворяющая условию Справедлива следующая теорема: Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля. Если условия теоремы выполнены, то матрица обратная к матрице
где Aij - алгебраические дополнения элементов aij данной матрицы A. Итак, чтобы найти обратную матрицу нужно: 1. Найти определитель матрицы A. 2. Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу 3. Найти матрицу, транспонированную полученной матрице Аналогично для матриц второго порядка, обратной будет следующая матрица Пример 9. 1. Найти матрицу, обратную данной | A | = 2. Найдем алгебраические дополнения элементов матрицы A.
Проверка:
Аналогично A∙A-1 = E. 2. Найти элементы
Вычислим | A | = 4. Тогда
3.
Матричный метод. Правило Крамера. Метод Гаусса. Пунтк 3. Правило Крамера. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы. Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат. Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна. Пример 11. Решить систему уравнений 1. Итак, х =1, у =2, z =3. 2. Решите систему уравнений при различных значениях параметра p: Система имеет единственное решение, если Δ ≠ 0.
1. При 2. При p = 30 получаем систему уравнений 3. При p = –30 система принимает вид Пункт 4. Метод Гаусса. Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы. Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а 21 и умножим на – а 11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а 31 и умножим на – а 11, а затем сложим с первым. В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на
Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1. При использовании метода Гаусса уравнения при необходимости можно менять местами. Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований. К элементарным преобразованиям матрицы относятся следующие преобразования: 1. перестановка строк или столбцов; 2. умножение строки на число, отличное от нуля; 3. прибавление к одной строке другие строки. Пример 12. Решить системы уравнений методом Гаусса. 1.
Вернувшись к системе уравнений, будем иметь
2. Выпишем расширенную матрицу системы и сведем ее к треугольному виду.
Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет. 3. Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
Вернемся к системе уравнений. Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
Таким образом, система имеет бесконечное множество решений.
МОДУЛЬ 1. ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |


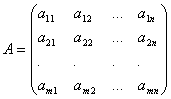 .
. , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
, называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом. .
.
 .
. или
или 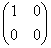 .
. .
. и
и  , то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
, то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22. , то
, то 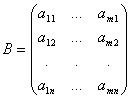 .
. .
.



 .
. - нельзя, т.к. размеры матриц различны.
- нельзя, т.к. размеры матриц различны. .
.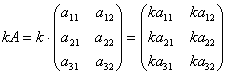 или
или  .
.

 .
. .
. ,
, 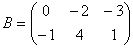 .
.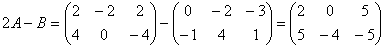 .
. Найти C =–3 A +4 B.
Найти C =–3 A +4 B.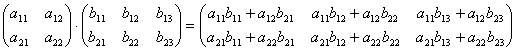 .
.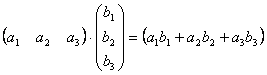 .
.

 .
. .
.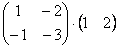 - нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
- нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
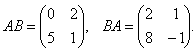

 , B·A – не имеет смысла.
, B·A – не имеет смысла. , то
, то .
. , раскладывая его по элементам 2-го столбца.
, раскладывая его по элементам 2-го столбца.
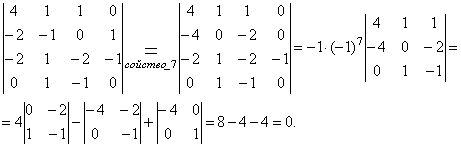
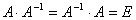 , где Е – единичная матрица.
, где Е – единичная матрица. находится следующим образом
находится следующим образом ,
, , элементами которой являются числа Aij.
, элементами которой являются числа Aij. – это и будет
– это и будет  .
. .
. . Сделать проверку.
. Сделать проверку.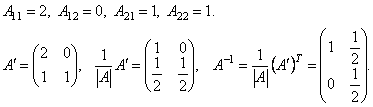
 .
. и
и  матрицы A-1 обратной данной
матрицы A-1 обратной данной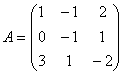 .
. .
.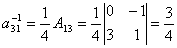 .
. . Найдем обратную матрицу.
. Найдем обратную матрицу.


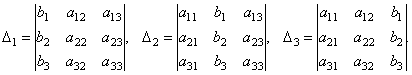
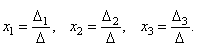
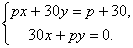
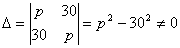 . Поэтому
. Поэтому 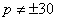 .
.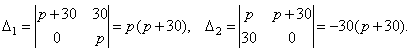
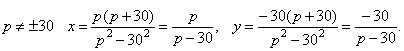
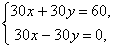 которая не имеет решений.
которая не имеет решений.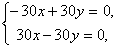 и, следовательно, имеет бесконечное множество решений x=y, yÎR.
и, следовательно, имеет бесконечное множество решений x=y, yÎR. .
.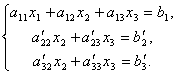
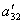 , умножим на
, умножим на  и сложим со вторым. Тогда будем иметь систему уравнений:
и сложим со вторым. Тогда будем иметь систему уравнений: