
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители третьего порядка.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим систему трех линейных уравнений с тремя неизвестными:
Матрица системы имеет вид:
где Определителем 3-го порядка называется коэффициент при неизвестных Вычисляется определитель 3-го порядка по правилу Саррюса:
Величины Пример 2. 1. Вычислить определитель по правилу Саррюса:
3.Элементарные сведения о перестановках. Рассмотрим п целых чисел (элементов) 1, 2,..., п. Их можно располагать в различном порядке. Определение 3.1: Всевозможные расположения чисел 1, 2, …, n называются перестановками. Перестановка Пример 3.1. При п =3 возможны перестановки (1 2 3), (1 3 2), (2 1 3), (2 3I), (3 1 2), (3 2 1). Их число равно 3! = 6. Определение 3.2: Факториалом n называется произведение первых n натуральных чисел. n!=1∙2∙…∙ n. Принято считать 0!=1. Методом математической индукции можно доказать, что из п элементов можно составить п!перестановок. Определение 3.3: Назовем беспорядком (или инверсией)в перестановке тот факт, что большее число стоит перед меньшим. Например, в перестановке (3 1 2 4) имеется два беспорядка; число 3 стоит перед числами 1 и 2. Определим число беспорядков в перестановках из трех элементов: в перестановке (1 2 3) — 0 беспорядков, (I 3 2) — 1, (2 1 3) — 1, (2 3 1) — 2, (3 1 2) — 2, (3 2 1) — 3. Число беспорядков в перестановке может быть четным или нечетным. Перестановки с четным числом беспорядков называются четными, перестановки с нечетным числом беспорядков называются нечетными. Так, перестановки (1 2 3), (2 3 1), (3 1 2) четные, а перестановки (1 3 2), Обмен местами двух элементов в перестановке называется транспозицией. Транспозиция переводит одну перестановку в другую. Одна транспозиция меняетчетность перестановки, т. е. четная перестановка становится нечетной, а нечетная четной. Для перестановки Теперь отметим закономерности при вычислении определителя 3-го порядка. 1. Число слагаемых равно 6=3!, то есть равно числу перестановок из 3-х элементов. 2. Каждое слагаемое является произведением 3-х элементов 3. Если перестановка Следовательно:
Для определителя второго порядка получим:
Определители n-го порядка. Очевидно, что для системы из n линейных уравнений с n неизвестными получим матрицу коэффициентов размером
Введем понятие определителя n -го порядка. Определение 4.1: Определителем n -го порядка называется число равное -сумме n! слагаемых; -каждое слагаемое есть произведение n элементов матрицы, взятых по одному из каждой строки и каждого столбца; -каждое слагаемое берется со знаком «+», если перестановка из вторых индексов четная, и со знаком «-», если перестановка из вторых индексов нечетная, при условии, что первые индексы образуют натуральный ряд чисел. Т.о. Здесь å берется по всем возможным перестановкам
5. Основные свойства определителей. Установим основные свойства определителей, которые для простоты будем показывать на определителе 2-го порядка. 1. При замене строк соответствующими столбцами (именуемой транспонированием) определитель остается неизменным. Действительно:
Следовательно, Примечание: Полученный выше результат дает нам право утверждать, что строки и столбцы определителя, именуемые в дальнейшем рядами, равноправны. 2. При перестановке двух рядов определитель меняет знак на противоположный. Действительно,
что и требовалось доказать. 3. Если в определителе два параллельных ряда одинаковы, то он равен нулю. Действительно, поменяем местами две одинаковых строки. Тогда величина определителя не изменится, а знак в силу свойства 2. поменяется. Единственное число, которое не меняется при изменении знака – ноль. 4. Общий множитель членов любого ряда можно вынести за знак определителя.
5. Если все элементы любого ряда являются суммами одинакового числа слагаемых, то определитель равен сумме определителей, в которых элементами рассматриваемого ряда служат отдельные слагаемые.
что и требовалось доказать. 6. Определитель не изменится, если к элементам любого ряда прибавить соответствующие элементы параллельного ряда, умноженные на некоторое число. Умножим вторую строку на
Действительно, в силу свойств 3,4,5
что и требовалось доказать.
6. Миноры и алгебраические дополнения элементов определителя. Рассмотрим определитель n -го порядка:
Выделим в определителе
Если в определителе Определение 6.1. А лгебраическим дополнением элемента
Пример 6.1. Найти минор
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 605; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |

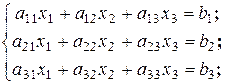
 . Решая систему методом исключения неизвестных, получим:
. Решая систему методом исключения неизвестных, получим:
 - некоторые числа.
- некоторые числа. и обозначается
и обозначается  .
.


 - элементы определителя (матрицы). В определителе различают строки, столбцы, главную диагональ из левого верхнего угла и побочную диагональ из правого верхнего угла. Первый индекс элемента
- элементы определителя (матрицы). В определителе различают строки, столбцы, главную диагональ из левого верхнего угла и побочную диагональ из правого верхнего угла. Первый индекс элемента 
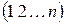 , в которой числа идут в порядке возрастания, называется натуральной.
, в которой числа идут в порядке возрастания, называется натуральной. количество беспорядков обозначают
количество беспорядков обозначают  , где
, где  -одно из чисел 1, 2,…, n;
-одно из чисел 1, 2,…, n;  , если
, если  .
. , где перестановка первых индексов элементов – натуральная перестановка (1,2,3), а вторых индексов (
, где перестановка первых индексов элементов – натуральная перестановка (1,2,3), а вторых индексов ( )- некоторая перестановка чисел 1,2,3; таким образом элементы
)- некоторая перестановка чисел 1,2,3; таким образом элементы  из разных строк и столбцов.
из разных строк и столбцов.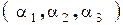 четная, то слагаемое берется со знаком «+», а если нечетная, то со знаком «-».
четная, то слагаемое берется со знаком «+», а если нечетная, то со знаком «-».

 :
:

 , составленным из чисел 1,2,…, n.
, составленным из чисел 1,2,…, n.


 , что и требовалось доказать.
, что и требовалось доказать. Поменяем местами строки и вычислим определитель
Поменяем местами строки и вычислим определитель ,
, что и требовалось доказать.
что и требовалось доказать.
 и прибавим ее к первой строке:
и прибавим ее к первой строке:
 =
=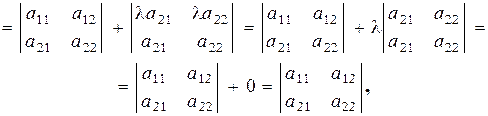
 .
. i -ю строку и j -й столбец. На пересечении этих рядов стоит элемент
i -ю строку и j -й столбец. На пересечении этих рядов стоит элемент 
 определителя
определителя  .
.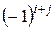 , и обозначается символом
, и обозначается символом  . Согласно определению получим
. Согласно определению получим .
. и алгебраическое дополнение
и алгебраическое дополнение  определителя
определителя 




