
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение определителей по элементам его рядов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1.Теорема разложения: Всякий определитель равен сумме парных произведений элементов какого-либо ряда на их алгебраические дополнения.
Для i- й строки:
или для j -го столбца:
Пример 7.1. Вычислить определитель разложением по элементам первой строки:
=1∙(1+12+12 +3∙(4+8+27 =8 Теорема разложения позволяет заменить вычисление одного определителя n- го порядка вычислением n определителей (n- 1)-го порядка. Однако для упрощения вычислений целесообразно для определителей высоких порядков использовать метод «размножения нулей», основанный на свойстве 6 раздела 5. Его идея: -сначала «размножить нули» в некотором ряду, т.е. получить ряд, в котором только один элемент не равен нулю, остальные нули; -затем разложить определитель по элементам этого ряда. Следовательно, на основании теоремы разложения исходный определитель равен произведению ненулевого элемента на его алгебраическое дополнение. Пример7.2. Вычислить определитель:
«Размножим нули» в первом столбце. От второй строки вычтем первую, умноженную на 2, от третьей строки вычтем первую, умноженную на 3, а от четвертой строки вычтем первую, умноженную на 4. При таких преобразованиях величина определителя не изменится.
По свойству 4 раздела 5 можем вынести
Следствие: Определитель с нулевым рядом равен нулю. 2. Теорема замещения: Сумма парных произведений каких-либо чисел на алгебраические дополнения некоторого ряда определителя равна тому определителю, который получается из данного, если в нем заменить элементы этого ряда взятыми числами. Для
1. Теорема аннулирования: Сумма парных произведений элементов какого-либо ряда на алгебраические дополнения параллельного ряда равна нулю.
Действительно, по теореме замещения получаем определитель, у которого в k -й строке стоят те же элементы, что и в i -й строке
Но по свойству 3 раздела 5 такой определитель равен нулю. Т.о., теорему разложения и ее следствия можно записать следующим образом:
8. Общие сведения о матрицах. Основные определения. Определение 8.1. Матрицей называется следующая прямоугольная таблица:
содержащая Применяют также следующие обозначения матрицы: Строки и столбцы матрицы именуются рядами. Величина Если в матрице поменять местами строки и столбцы, то получим матрицу, называемую транспонированной. Матрица, транспонированнаяс Например: Определение 8.2. Две матрицы A и B называются равными, если 1) обе матрицы одинаковых размеров, т.е. 2) все их соответствующие элементы равны, т.е.
Тогда Здесь одно матричное равенство (8.2) эквивалентно
9. Разновидности матриц. 1) Матрица, все элементы которой равны нулю, называется ноль-матрицей:
2) Если матрица состоит только из одной строки, то она называется матрицей-строкой, например Транспонирование переводит матрицу-столбец в матрицу-строку и наоборот. 3) Если m = n, то матрица называется квадратной матрицей n-го порядка. Диагональ членов квадратной матрицы, идущая из левого верхнего угла в ее правый нижний угол, называется главной. Другая же диагональ ее членов, идущая из левого нижнего угла в ее правый верхний угол, именуется побочной. Для квадратной матрицы может быть вычислен определитель det(A). 4) Если определитель матрицы равен нулю, то матрица называется особенной, или вырожденной. В противном случае матрица именуется неособенной, или невырожденной. 5) Разновидности квадратных матриц: Если все элементы квадратной матрицы, за исключением элементов ее главной диагонали, равны нулю, то матрица называется диагональной. Диагональная матрица имеет вид: Ее определитель равен произведению элементов главной диагонали: В частности, при При
Если все элементы квадратной матрицы по одну сторону главной диагонали равны нулю, то матрица именуется треугольной (соответственно верхней или нижней).
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 3242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.27.24 (0.009 с.) |

 ;
;


 )
) 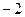 ∙(2+16+18
∙(2+16+18  )+
)+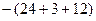 )
) 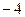 ∙(8+4+18
∙(8+4+18  )=
)= =
=  .
. .
.
 за знак определителя из 1-го столбца,
за знак определителя из 1-го столбца,  из 2-го столбца и
из 2-го столбца и  из 3-го столбца.
из 3-го столбца.

 -й строки:
-й строки:
 .
.

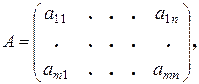
 элементов
элементов  ,расположенных в т строках и в п столбцах.
,расположенных в т строках и в п столбцах. , или
, или  , или
, или  .
. называется размером матрицы.
называется размером матрицы. , обычно обозначается символом
, обычно обозначается символом  .
.
 и
и  ;
; (8.1)
(8.1) . (8.2)
. (8.2)
 . Аналогично этому матрица, имеющая только один столбец, именуется матрицей-столбцом, например
. Аналогично этому матрица, имеющая только один столбец, именуется матрицей-столбцом, например  .
.
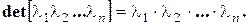
 диагональная матрица называется скалярной:
диагональная матрица называется скалярной: 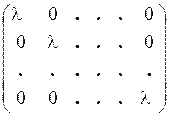 .
. 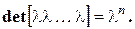
 скалярная матрица называется единичной и обозначается символом Е.
скалярная матрица называется единичной и обозначается символом Е. . Ее определитель равен единице:
. Ее определитель равен единице: 
 - верхняя треугольная матрица.
- верхняя треугольная матрица.



