
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные векторы и собственные значения.Содержание книги
Поиск на нашем сайте
Рассмотрим
где В матричной форме это преобразование принимает вид
где Определение 21.1: Закон вида (21.1), задающий линейное преобразование любого вектора Пример 21.1. Пусть задана матрица линейного преобразования Если Рассмотрим преобразование
Тогда, подставив (21.3) в (21.2), имеем матричное уравнение
Определение 20.2: ненулевой вектор Для нахождения собственного вектора
Получили однородную систему
Необходимым и достаточным условием существования ненулевого решения такой системы является равенство нулю определителя матрицы этой системы, то есть
Если вычислить определитель этой матрицы, то он будет зависеть от
Пример 21.1. Зададимся матрицей преобразования
Эта система имеет ненулевое решение, если ее определитель равен нулю, т.е.
и для нахождения собственных значений приравняем его к нулю.
Найдем собственный вектор при
Пусть При Рекомендуемая литература 1. Клиот - Дашинский М.И. Алгебра матриц и векторов. СПб.: Издательство «Лань», 1998. 2. Клиот-Дашинский М.И. Линейная алгебра. Методические указания к выполнению самостоятельной работы для студентов I курса. Л.: ЛИСИ, 1988. 3. Боревич З.И. Определители и матрицы. М.: «Наука», 1988. 4. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. Ростов-на-Дону: «Феникс», 1997. Содержание 1. Определители второго порядка…………………………………………………….…..……3 2. Определители третьего порядка………………………………………………………………3 3.Элементарные сведения о перестановках……………………………………………………...5 4.Определители n-го порядка…………………………………………………...……………6 5. Основные свойства определителей……………………………………………………………7 6. Миноры и алгебраические дополнения элементов определителя………………………...8 7. Разложение определителей по элементам его рядов……………………………….……9 8. Общие сведения о матрицах. Основные определения…………………..……………..12 9. Разновидности матриц……………………………………………………………………..13 10. Арифметические операции над матрицами……………………………..…..…………15 11. Свойства перемножения матриц…………………………………………...…………...16 12. Обратная матрица и ее вычисление с помощью союзной матрицы……….……….18 13.Cистемы линейных уравнений………………………………………………………….....…20 14.Матричная запись системы уравнений………………………………………...……..……...21 15. Системы с неособенной квадратной матрицей. Формулы Крамера………………….........22
16. Системы уравнений в базисной форме…………………..…………………….………24 17.Метод Гаусса………………………………………………………………………………….26 18.Нахождение решения в базисной форме……………………………………….…..…..32 19. Вычисление обратной матрицы по схеме Гаусса………………………….…………….….33 20.Понятие об 21. Линейное преобразование векторов. Собственные векторы и собственные значения…………………………………………………………………………………………….37 Лидия Евсеевна Морозова Ольга Валентиновна Соловьева
ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Редактор Корректор
Подписано к печати 00.00.2005. Формат 60x84 1/16. Бум. Офсетная. Усл. печ. л.. Уч.-изд. л.. Тираж 500 экз. Заказ.»С». Санкт-Петербургский государственный архитектурно-строительный университет. 198005, Санкт-Петербург, 2-ая Красноармейская, 4. Отпечатано на ризографе. 198005, Санкт-Петербург, 2-ая Красноармейская, 5.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.216.107 (0.009 с.) |

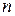 -мерные векторы
-мерные векторы  и
и 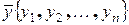 , координаты которых связаны зависимостью
, координаты которых связаны зависимостью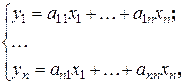 (21.1)
(21.1)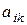 - любые скаляры. Тогда говорят, что вектору
- любые скаляры. Тогда говорят, что вектору 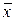 ставится в соответствие вектор
ставится в соответствие вектор  по закону (21.1). Или:
по закону (21.1). Или: 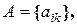 где
где 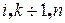 .
.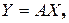 (21.2)
(21.2)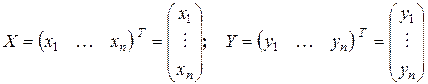 .
.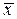
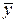 этого же пространства называется линейным преобразованием.
этого же пространства называется линейным преобразованием.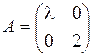 , где
, где 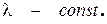 Возьмем произвольный вектор
Возьмем произвольный вектор 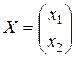 и найдем образ
и найдем образ 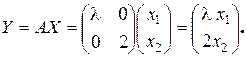
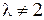 , то вектор
, то вектор 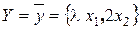 . Следовательно, вектор
. Следовательно, вектор  , то вектор
, то вектор 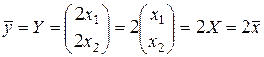 , а это значит, что
, а это значит, что 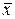 изменит только длину.
изменит только длину.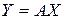 с заданной матрицей
с заданной матрицей  . Будем искать такой вектор
. Будем искать такой вектор 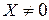 , который в результате линейного преобразования меняет длину, но не меняет направление исходного вектора, т.е.
, который в результате линейного преобразования меняет длину, но не меняет направление исходного вектора, т.е. 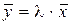 или, в матричной форме,
или, в матричной форме, . (21.3)
. (21.3)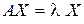 (21.4)
(21.4)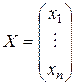 называется собственным вектором матрицы
называется собственным вектором матрицы 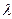 - некоторое число. При этом
- некоторое число. При этом  называется собственным значением матицы
называется собственным значением матицы 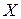 решим уравнение (21.4).
решим уравнение (21.4).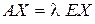 , т.к.
, т.к. 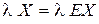 , где
, где 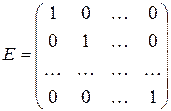 - единичная матрица, играющая роль единицы в матричном исчислении. Тогда
- единичная матрица, играющая роль единицы в матричном исчислении. Тогда 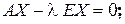
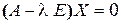 . (21.5)
. (21.5)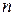 линейных уравнений относительно неизвестных координат
линейных уравнений относительно неизвестных координат 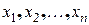 собственного вектора
собственного вектора  . Матрица
. Матрица 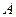 , у которой из элементов главной диагонали вычли число
, у которой из элементов главной диагонали вычли число 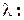
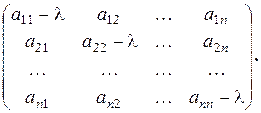
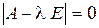 . (21.6)
. (21.6)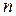 . Его называют характеристическим многочленом, а равенство (21.6) – характеристическим уравнением. Решая уравнение (21.6), находят собственные значения
. Его называют характеристическим многочленом, а равенство (21.6) – характеристическим уравнением. Решая уравнение (21.6), находят собственные значения 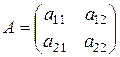 характеристическое уравнение имеет вид
характеристическое уравнение имеет вид 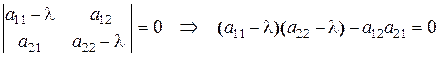 , то есть вид квадратного уравнения относительно неизвестного собственного значения
, то есть вид квадратного уравнения относительно неизвестного собственного значения 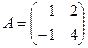 и найдем собственный вектор
и найдем собственный вектор 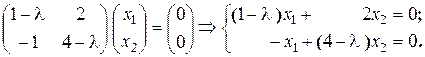 (21.7)
(21.7)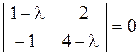 . Вычислим характеристический многочлен
. Вычислим характеристический многочлен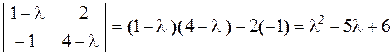


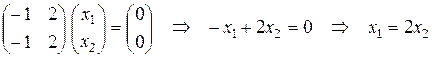 .
.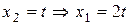 . Тогда собственный вектор имеет вид
. Тогда собственный вектор имеет вид 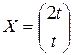 .
.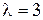 система (21.7) имеет матричный вид
система (21.7) имеет матричный вид 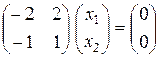 , а, следовательно, можно записать, что
, а, следовательно, можно записать, что 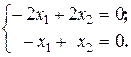 Решение получается в базисной форме
Решение получается в базисной форме 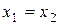 и, полагая
и, полагая 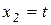 , найдем собственный вектор
, найдем собственный вектор 
 -мерном арифметическом пространстве и
-мерном арифметическом пространстве и 


