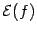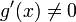Направление вогнутости графика функции. Точки перегиба.

Полное иследование функции и построение графика.

 

 

Стоит задача: провести полное исследование функции и построить ее график:

 

 

 

Каждый студент прошел через подобные задачи.

 

Дальнейшее изложение предполагает хорошее знание свойств и графиков основных элементарных функций. Рекомендуем обращаться к этому разделу при возникновении вопросов.

 

Алгоритм исследования функции состоит из следующих шагов.

1. Нахождение области определения функции.

Это очень важный шаг исследования функции, так как все дальнейшие действия будут проводиться на области определения.

 

В нашем примере нужно найти нули знаменателя и исключить их из области действительных чисел.

 

В других примерах могут быть корни, логарифмы и т.п. Напомним, что в этих случаях область определения ищется следующим образом:

для корня четной степени, например,

 

 

- область определения находится из неравенства

 

 

для логарифма

 

 

- область определения находится из неравенства

.

 

Общая схема исследования графика функции.

Пусть дана функция

Для её исследования нужно:

1). Найти её область определения

 

Если это не слишком сложно, то полезно найти также область значений

 

 

 

(Однако, во многих случаях, вопрос нахождения

 

откладывается до нахождения экстремумов функции.)

 

2). Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной (быть может, после сдвига влево или вправо по оси), не является ли она периодической.

 

3). Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения

 

 

, если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.

Пусть

 

Эта функция определена на всей числовой оси, однако 0 является точкой разрыва функции: при

 

 

функция стремится к

 

 

Значит, вертикальная прямая

 

 

служит вертикальной асимптотой функции, хотя функция и определена в точке

 

 

Если область определения

 

включает в себя лучи вида

 

 

или

 

 

, то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при

 

 

или

 

соответственно.

 

Правило Лопиталя.

Правило Бернулли-Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида.

И

Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Точная формулировка:

Условия:

Или

f(x) и g(x) дифференцируемы в проколотой окрестности a;

в проколотой окрестности a;

существует

тогда существует

 

 

 

Пределы также могут быть односторонними.