
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимое и достаточное условия существования функции 2-х переменных.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема 46.1 (необходимые условия экстремума). Если в точке N(x0;y0) дифференцируемая функция z=ƒ(х;у) имеет экстремум, то ее частные производные в этой точке равны нулю: ƒ'x(х0;у0)=0, ƒ'y(х0;у0)=0.
Зафиксируем одну из переменных. Положим, например, у=у0. Тогда получим функцию ƒ(х;у0)=φ(х) одной переменной, которая имеет экстремум при х = х0. Следовательно, согласно необходимому условию экстремума функции одной переменной (см. п. 25.4), φ'(х0) = 0, т. е. ƒ'x(х0;y0)=0.
Аналогично можно показать, что ƒ'y(х0;у0) = 0.
Геометрически равенства ƒ'x(х0;у0)=0 и ƒ'y(х0;у0)=0 означают, что в точке экстремума функции z=ƒ(х;у) касательная плоскость к поверхности, изображающей функцию ƒ(х;у), параллельна плоскости Оху, т. к. уравнение касательной плоскости есть z=z0 (см. формулу (45.2)).
Замечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например, функция
Точка, в которой частные производные первого порядка функции z ≈ ƒ(х; у) равны нулю, т. е. f'x=0, f'y=0, называется стационарной точкой функ ции z.
Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.
В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию z = ху. Для нее точка О(0; 0) является критической (в ней z'x=у и z'y — х обращаются в ноль). Однако экстремума в ней функция z=ху не имеет, т. к. в достаточно малой окрестности точки О(0; 0) найдутся точки для которых z>0 (точки I и III четвертей) и z < 0 (точки II и IV четвертей).
Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию. Теорема 46.2 (достаточное условие экстремума). Пусть в стационарной точке (хо;уо) и некоторой ее окрестности функция ƒ(х;у) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (х0;у0) значения A=f''xx(x0;y0), В=ƒ''xy(х0;у0), С=ƒ''уy(х0;у0). Обозначим
1. если Δ > 0, то функция ƒ(х;у) в точке (х0;у0) имеет экстремум: максимум, если А < 0; минимум, если А > 0;
2. если Δ < 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.
В случае Δ = 0 экстремум в точке (х0;у0) может быть, может не быть. Необходимы дополнительные исследования.
Примем без доказательства. 28. Понятие неопределенного интеграла. Основные свойства неопределенного интеграла Неопределенным интегралом Неопределенным интегралом от функции f(x) наз.совокупность всех её первообразных
Основные свойства неопределенного интеграла. 10. ( Производная от интеграла равна подынтегральной функции. 20. d ( Дифференциал от интеграла равен подынтегральному выражению 30. Интеграл от дифференциала функции дает функцию плюс константа. 40. Постоянный множитель выносится за знак интеграла. 50. Интеграл от суммы функций равен сумме интегралов.
60. Инвариантность формы неопределенного интеграла: Переменную интегрирования х можно заменить в интеграле на произвольную дифференцируемую функцию u=u(x), т.е. если
29. Основные методы интегрирования неопределенного интеграла 1. Метод введения нового аргумента. Если
2. Метод разложения. Если 3. Метод подстановки. Если 4. Метод интегрирования по частям. Если
30. Интегрирование дробно-рациональной функции.
31. Интегрирование тригонометрических функций. Интегралы типа Используем метод подведения функции под знак дифференциала
= Пр.
Интегралы типа Метод понижения степени по формулам sin2x = ½ (1 – cos 2x); cos2x = ½ (1 + cos 2x); sin x cos x = ½ sin 2x или замена tg x = t (см. ниже) Пр.
Интегралы типа
sin a cos b = ½[sin(a+b) + sin(a-b)]; cos a cos b = ½[cos(a+b) + cos(a-b)] sin a sin b = ½[cos(a-b) – cos(a+b)] Пр.
Интегралы типа
cos2x = Пр. = t2/2 - ½ Пр. Универсальная замена tg x/2 = t в интегралах и приходим к интегралу от рациональной алгебраической дроби. { sin x = 2sin x/2 cos x/2 = 2 cos x = cos2x/2 – sin2x/2 = cos2x/2 (1 - Пр. = 2
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 998; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 имеет максимум в точке О(0;0) (см. рис. 211), но не имеет в этой точке частных производных.
имеет максимум в точке О(0;0) (см. рис. 211), но не имеет в этой точке частных производных. Тогда:
Тогда: называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е.
называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е.  или
или 
 dF(x) =
dF(x) =  то
то  где
где  — непрерывно дифференцируемая функция.
— непрерывно дифференцируемая функция.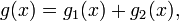 то
то 
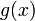 — непрерывна, то, полагая
— непрерывна, то, полагая  где
где 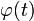 непрерывна вместе со своей производной
непрерывна вместе со своей производной  , получим
, получим 
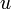 и
и  — некоторые дифференцируемые функции от
— некоторые дифференцируемые функции от  , то
, то

 =
=  = -
= -  = -
= - 
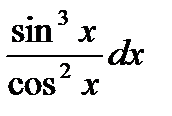
 = (1 + tg2x) dx = dt
= (1 + tg2x) dx = dt  dx = dt/(1+t2), x = arctg t
dx = dt/(1+t2), x = arctg t =
=  , sin2x = (1 – cos2x) =
, sin2x = (1 – cos2x) = 
 =
=  =
=  , cos x =
, cos x =  , dx =
, dx = 
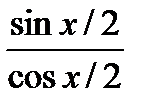 cos2x/2 =
cos2x/2 =  ) = cos2x/2 (1 – t2) =
) = cos2x/2 (1 – t2) =  = { 1 + sin x = 1 +
= { 1 + sin x = 1 +  } = 2
} = 2  =
= = 2
= 2  =
=  + C
+ C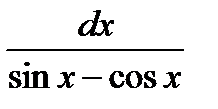 ;
; 



