
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремум функции нескольких переменныхСодержание книги
Поиск на нашем сайте
Определение. Пусть функция
то точка Определение. Точки локального максимума и локального минимума функции Теорема. (Необходимые условия экстремума). Пусть функция
Эта точка Теорема. (Достаточные условия экстремума). Пусть в окрестности критической точки
1) Если 2) Если В случае если Условный экстремум
Условный экстремум находится, когда переменные х и у, входящие в функцию
В этом случае из переменных х и у только одна является независимой, т.к. другая может быть выражена через нее из уравнения связи. Тогда
В точках экстремума:
Кроме того:
Умножим равенство (2.2) на число l и сложим с равенством (2.1).
Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум. Выражение Пример. Найти экстремум функции
Таким образом, функция имеет экстремум в точке Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа. Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.
Производная по направлению
Рассмотрим функцию Построим вектор Расстояние между точками
Высказанные выше предположения, проиллюстрируем на рисунке:
M
M1
y x Предположим, что функция
где величины Из геометрических соображений очевидно:
Таким образом, приведенные выше равенства могут быть представлены следующим образом:
Величина Пример. Вычислить производную функции Решение. Определяем координаты вектора
Находим модуль этого вектора:
Находим частные производные функции
Значения этих величин в точке А равны: Для нахождения направляющих косинусов вектора
В качестве вектора
Окончательно находим:
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 определена в некоторой области
определена в некоторой области  , и
, и  - произвольная точка этой области. Если для всех точек
- произвольная точка этой области. Если для всех точек  из некоторой окрестности точки
из некоторой окрестности точки 

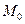 называется точкой локального максимума (локального минимума) функции
называется точкой локального максимума (локального минимума) функции  в области
в области  .
. называется критической точкой функции
называется критической точкой функции 
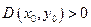 , то в точке
, то в точке  - максимум, если
- максимум, если  - минимум.
- минимум. , то в точке
, то в точке  , вывод о наличии экстремума сделать нельзя.
, вывод о наличии экстремума сделать нельзя. , не являются независимыми, т.е. существует некоторое соотношение
, не являются независимыми, т.е. существует некоторое соотношение , которое называется уравнением связи.
, которое называется уравнением связи. становится функцией одного переменного. Следовательно,
становится функцией одного переменного. Следовательно,
 (2.1)
(2.1) (2.2)
(2.2)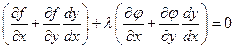 ,
, .
.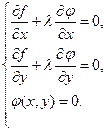
 называется функцией Лагранжа.
называется функцией Лагранжа. , если уравнение связи:
, если уравнение связи:  . Имеем
. Имеем ;
;


 .
. в точках
в точках  и
и  .
. . Углы наклона этого вектора к положительным направлениям координатных осей
. Углы наклона этого вектора к положительным направлениям координатных осей  обозначим соответственно
обозначим соответственно  . Косинусы этих углов называются направляющими косинусами вектора
. Косинусы этих углов называются направляющими косинусами вектора  .
. и
и  обозначим через
обозначим через 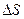 :
: .
. z
z и
и  . Тогда справедливо равенство:
. Тогда справедливо равенство: ,
, – бесконечно малые при
– бесконечно малые при  функции.
функции.
 ;
; .
. является скалярной. Она определяет направление вектора
является скалярной. Она определяет направление вектора  называется производной функции
называется производной функции  по направлению вектора
по направлению вектора  .
. в точке
в точке 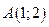 по направлению вектора
по направлению вектора 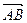 :
:  .
. 2
2  .
. =
=  .
.
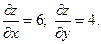

 ;
;  .
. - значение производной заданной функции по направлению вектора
- значение производной заданной функции по направлению вектора 


