Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 6. Дифференциальное исчисление функции нескольких переменныхСодержание книги
Поиск на нашем сайте
Раздел 6. Дифференциальное исчисление функции нескольких переменных Предел и непрерывность функции нескольких переменных
При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты остаются справедливыми для функций произвольного числа переменных. Пусть дано множество Функцию Пример. На множестве Графиком функции Расстоянием между двумя произвольными точками
Множество точек Открытый круг радиуса Определение. Точка Определение. Точка Замечание. Граничная точка множества может как принадлежать этому множеству, так и не принадлежать ему. Определение. Множество Определение. Множество Пример. Если Определение. Точка Замечание. Предельная точка множества может принадлежать, а может не принадлежать этому множеству. Пример. Множество
Непрерывность функции нескольких переменных
Пусть дана функция Определение. Говорят, что функция 1) 2) Сформулируем определение непрерывности в эквивалентной форме. С этой целью обозначим Определение. Говорят, что функция
Теорема. Если функции Определение. Функция Определение. Множество 1) является открытым множеством, т.е. содержит каждую свою точку вместе с некоторой своей Если Определение. Говорят, что функция
Частные производные и дифференциал функции нескольких переменных Геометрический смысл полного дифференциала. Экстремум функции нескольких переменных
Условный экстремум
Условный экстремум находится, когда переменные х и у, входящие в функцию
В этом случае из переменных х и у только одна является независимой, т.к. другая может быть выражена через нее из уравнения связи. Тогда
В точках экстремума:
Кроме того:
Умножим равенство (2.2) на число l и сложим с равенством (2.1).
Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум. Выражение Пример. Найти экстремум функции
Таким образом, функция имеет экстремум в точке Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа. Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.
Производная по направлению
Рассмотрим функцию Построим вектор Расстояние между точками
Высказанные выше предположения, проиллюстрируем на рисунке:
M
M1
y x Предположим, что функция
где величины Из геометрических соображений очевидно:
Таким образом, приведенные выше равенства могут быть представлены следующим образом:
Величина Пример. Вычислить производную функции Решение. Определяем координаты вектора
Находим модуль этого вектора:
Находим частные производные функции
Значения этих величин в точке А равны: Для нахождения направляющих косинусов вектора
В качестве вектора
Окончательно находим:
Раздел 6. Дифференциальное исчисление функции нескольких переменных
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.166.193 (0.009 с.) |

 , и пусть указано правило (закон), по которому каждой точке
, и пусть указано правило (закон), по которому каждой точке  ставится в соответствие единственное действительное число
ставится в соответствие единственное действительное число  . В этом случае говорят, что задана функция
. В этом случае говорят, что задана функция  с областью определения
с областью определения  и областью значений
и областью значений  . При этом
. При этом  и
и  называют независимыми переменными (аргументами), а
называют независимыми переменными (аргументами), а  – зависимой переменной (функцией).
– зависимой переменной (функцией). .
. определим функцию
определим функцию  ; тогда ее областью значений является отрезок
; тогда ее областью значений является отрезок 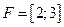 . Эту функцию можно определить, конечно, и на всей плоскости
. Эту функцию можно определить, конечно, и на всей плоскости  ; в этом случае имеем
; в этом случае имеем  и
и  . Обычно графиком функции является некоторая поверхность.
. Обычно графиком функции является некоторая поверхность. и
и  евклидова пространства
евклидова пространства  , определяемое формулой:
, определяемое формулой: .
. называется открытым кругом радиуса
называется открытым кругом радиуса  с центром в точке
с центром в точке  ,
,  – окружностью радиуса
– окружностью радиуса  с центром в точке
с центром в точке  , если существует
, если существует  -окрестность
-окрестность  точки
точки  ).
). ). Заметим, что множество
). Заметим, что множество  является замкнутым и называется замыканием множества
является замкнутым и называется замыканием множества  , то
, то  . При этом
. При этом  .
. .
. совпадает с множеством своих предельных точек. Множество
совпадает с множеством своих предельных точек. Множество  имеет единственную предельную точку
имеет единственную предельную точку  .
. – предельная точка множества
– предельная точка множества 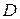 .
.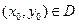 ;
; , т.е.
, т.е.  .
. ,
,  и
и  .
. .
. и
и  непрерывны в точке
непрерывны в точке  ,
, 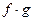 , а если
, а если  , то и функция
, то и функция  .
. называется непрерывной на множестве
называется непрерывной на множестве  если она непрерывной в каждой точке множества
если она непрерывной в каждой точке множества  -окрестностью; 2) является линейно связным множеством, т.е. для любых двух различных точек
-окрестностью; 2) является линейно связным множеством, т.е. для любых двух различных точек  существует ломаная, соединяющая
существует ломаная, соединяющая  и
и  и целиком лежащая в
и целиком лежащая в  называют замкнутой областью.
называют замкнутой областью. непрерывна в области
непрерывна в области  , не являются независимыми, т.е. существует некоторое соотношение
, не являются независимыми, т.е. существует некоторое соотношение , которое называется уравнением связи.
, которое называется уравнением связи. становится функцией одного переменного. Следовательно,
становится функцией одного переменного. Следовательно,
 (2.1)
(2.1) (2.2)
(2.2)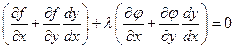 ,
, .
.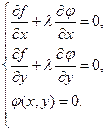
 называется функцией Лагранжа.
называется функцией Лагранжа. , если уравнение связи:
, если уравнение связи:  . Имеем
. Имеем ;
;


 .
. в точках
в точках  и
и  .
. . Углы наклона этого вектора к положительным направлениям координатных осей
. Углы наклона этого вектора к положительным направлениям координатных осей  обозначим соответственно
обозначим соответственно  . Косинусы этих углов называются направляющими косинусами вектора
. Косинусы этих углов называются направляющими косинусами вектора  .
. :
: .
. z
z и
и  ,
, – бесконечно малые при
– бесконечно малые при  функции.
функции.
 ;
; .
. является скалярной. Она определяет направление вектора
является скалярной. Она определяет направление вектора  называется производной функции
называется производной функции  по направлению вектора
по направлению вектора  .
. в точке
в точке 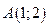 по направлению вектора
по направлению вектора 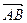 :
:  .
. 2
2  .
. =
=  .
.
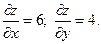

 ;
;  .
. - значение производной заданной функции по направлению вектора
- значение производной заданной функции по направлению вектора