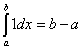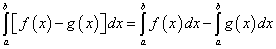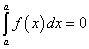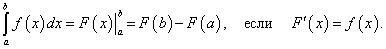Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимое условие экстремумаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопросы к экзамену 1 курс, 2 семестр, ФАУ, 341-345гр. Дисциплина – «математика», Менеджмент, бакалавриат.
Теорема Ролля
Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения) Пусть функция 1. непрерывна на отрезке 2. дифференцируема на интервале 3. на концах отрезка Тогда на интервале Следствие. (Геометрический смысл теоремы Ролля) Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс. Следствие. Если
Теорема 2. (Теорема Лагранжа) Теорема Лагранжа. (О конечных приращениях) Пусть функция 1. непрерывна на отрезке 2. дифференцируема на интервале Тогда на интервале
Замечание Теорема Ролля есть частный случай теоремы Лагранжа, когда Следствие. (Геометрический смысл теоремы Лагранжа) На кривой
Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:
3 Теорема Коши Теорема Коши. (Об отношении конечных приращений двух функций) Если функции 1. непрерывны на отрезке 2. дифференцируемы на интервале 3. производная тогда на этом интервале найдется по крайней мере одна точка
Теорема Если производная функции равна нулю на некотором промежутке, то функция является постоянной на этом промежутке. Теорема Если две функции имеют равные производные на некотором промежутке, то они на этом промежутке отличаются друг от друга на некоторое слагаемое.
4 Правило Лопиталя (раскрытие неопределенности) (Правило Лопиталя). Пусть функции 1) эти функции дифференцируемы в окрестности точки 2) 3) 4) Тогда существует и Таким образом, вычисление предела отношения двух функций может быть заменено при выполнении условий теоремы вычислением предела отношения производных этих функций. Замечание Правило Лопиталя распространяется на случай неопределенности типа Правило Лопиталя распространяется и на случай Замечание Иногда правило Лопиталя приходится применять несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы на каждом шаге должны оставаться справедливыми. Замечание Хотя правило Лопиталя работает только с неопределенностями Задание. Найти Решение. Получим неопределенность не подходящую под правило Лопиталя, приведем ее к нужному виду и для решения предела воспользуемся правилом Лопиталя.
Ответ.
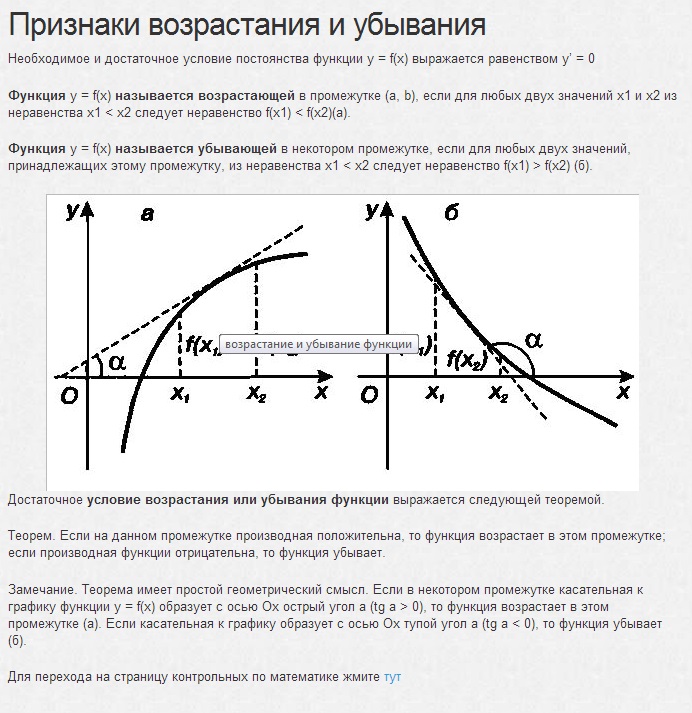
5 Постоянство, убывание и возрастание
Если производная функции на участке существует и равна нулю и функция определена на данном участке, то функция на данном участке постоянна. Одним из важнейших приложений дифференцированного исчисления является исследование функции с целью построения ее графика.
6 Экстремум функции Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Теорема (Необходимое условие экстремума) Если функция Точки, в которых производная равна нулю: Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения Замечание Не в каждой своей критической точке функция обязательно имеет максимум или минимум. Точка Точка
7 Достаточные условия экстремума функции. Теорема (Первое достаточное условие экстремума) Пусть для функции 1. функция непрерывна в окрестности точки 2. 3. производная Тогда в точке Если производная Таким образом, для того чтобы исследовать функцию 1. найти производную 2. найти критические точки, то есть такие значения 3. исследовать знак производной слева и справа от каждой критической точки; 4. найти значение функции в экстремальных точках. Теорема (Второе достаточное условие экстремума) Пусть для функции 1. она непрерывна в окрестности точки 2. первая производная 3. Тогда в точке Теорема (Об условиях выпуклости или вогнутости графика функции) Пусть функция Определение Точкой перегиба графика функции Теорема (О необходимом условии существования точки перегиба) Если функция Теорема (О достаточном условии существования точки перегиба) Если: 1. первая производная 2. вторая производная 3. тогда в точке Виды асимптот Определение Прямая Замечание. Прямая Определение Прямая Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую. Определение Прямая Теорема (условиях существования наклонной асимптоты) Если для функции Замечание Горизонтальная асимптота является частным случаем наклонной при Замечание Если при нахождении горизонтальной асимптоты получается, что Замечание Кривая
10 Схема исследования и построения графика функции. При построении графика функции необходимо провести ее предварительное исследование. Примерная схема исследования функции с целью построения ее графика имеет следующую структуру: 1. Область определения 2. Четность, нечетность функции. 3. Точки пересечения с осями. 4. Асимптоты функции. 5. Экстремумы и интервалы монотонности. 6. Точки перегиба и промежутки выпуклости, вогнутости. 7. Сводная таблица. Замечание Схема представлена как примерная. Пункты исследования можно опускать, если они дают банальную информацию, или переставлять, если обнаруживаются интересные особенности поведения графика. Замечание Для уточнения графика можно найти некоторые дополнительные точки, но иногда удается обойтись и без них. Замечание Рекомендуется строить график одновременно с исследованием функции, нанося на координатную плоскость информацию по завершении каждого пункта исследования.
Задание. Исследовать функцию Решение. 1) Область определения функции.
2) Четность, нечетность.
Функция общего вида. 3) Точки пересечения с осями. а) с осью
то есть точки б) с осью 4) Асимптоты. а) вертикальные: прямые б) горизонтальные асимптоты:
то есть прямая в) наклонные асимптоты
Таким образом, наклонных асимптот нет. 5) Критические точки функции, интервалы возрастания, убывания.
Найдем точки, в которых первая производная равна нулю или не существует:
Таким образом, функция убывает на всей области существования. Точек экстремума нет. 6) Точки перегиба, интервалы выпуклости, вогнутости.
Найдем точки, в которых вторая производная равна нулю или не существует:
Таким образом, на промежутках 7) Эскиз графика.
11 Понятие первообразной функции и неопределенного интеграла. Первообразная, основные понятия и определения Определение Функция
Последнее равенство можно записать через дифференциалы:
Пример Функция
Первообразная Теорема (О бесконечном множестве первообразных для функции) Если функция Неопределенный интеграл Определение Совокупность всех первообразных функции
Знак Операция нахождения первообразной или неопределенного интеграла от функции
12 Свойства неопределенного интеграла 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению
Пример
Больше примеров решений→ 2. Производная от неопределенного интеграла равна подынтегральной функции
Пример
Больше примеров решений→ 3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
Пример
Больше примеров решений→ 4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла
Пример
Больше примеров решений→ 5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций
Пример
Больше примеров решений→ 6. Если Пример Известно, что
13 Таблица основных интегралов
Метод непосредственного интегрирования Определение Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. Таким образом, алгоритм действий следующий: 1. тождественное преобразование подынтегральной функции; 2. применение свойств неопределенного интеграла: вынесение константы за знак интеграла, представление интеграла от суммы функций в вид суммы интегралов; 3. использование таблицы интегралов. В простейших примерах для применения непосредственного интегрирования достаточно разложить подынтегральную функцию на слагаемые и постоянные величины вынести за знак интеграла. При определенной практике интегрирования обычно эти действия проводят устно, записывая лишь результат интегрирования. Задание. Найти интеграл Решение. Воспользуемся свойствами интеграла и приведем данный интеграл к нескольким табличным.
14 Метод внесения новой переменной под знак дифференциала Пусть требуется найти неопределенный интеграл
Тогда
Указанное преобразование подынтегрального выражения называют подведением под знак дифференциала. Тогда, если
Замечание. При интегрировании методом подведения под знак дифференциала полезны следующие равенства для дифференциалов:
Замечание В некоторых случаях формулу интегрирования частями нужно применять неоднократно.
18 интегрирование неправильных рациональных дробей
19 разложение правильной дроби
Интегрирование правильных рациональных дробей Рациональная дробь Пример Рациональная дробь Выражения Если дробь неправильная, то, разделив числитель на знаменатель по правилу деления многочленов, можно получить многочлен плюс правильную дробь. Примеры интегрирования правильных рациональных дробей Пример Задание. Представить неправильную дробь Решение. Поделим числитель на знаменатель дроби в столбик (деление проводится до тех пор, пока степень остатка не будет меньше степени делителя):
Таким образом,
Ответ. Пример Задание. Найти интеграл Решение. Так как подынтегральная функция
То есть,
Тогда интеграл
Ответ. 20 понятие определенного интеграла Определённым интегралом от непрерывной функции f (x) на конечном отрезке [ a, b ] (где
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [ a, b ] – отрезком интегрирования. Таким образом, если F (x) – какая-нибудь первообразная функция для f (x), то, согласно определению,
При a = b по определению принимается
Равенство (38) называется формулой Ньютона-Лейбница. Разность F (b) – F (a) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
21 Геометрический смысл определенного интеграла. Определённый интеграл
Свойства определенного интеграла 1.Определенный интеграл от единицы равен длине интервала интегрирования:
2.Постоянный множитель можно выносить за знак определенного интеграла:
3.Определенный интеграл от суммы функций равен сумме интегралов от этих функций:
4.Определенный интеграл от разности функций равен разности интегралов от этих функций:
5.Если верхний предел равен нижнему, то определенный интеграл равен нулю:
6.При перестановке пределов интегрирования определенный интеграл изменяет знак на противоположный:
7.Пусть точка c принадлежит отрезку [ a, b ]. Тогда определенный интеграл от функции f (x) на отрезке[ a, b ] равен сумме интегралов на частичных промежутках [ a, c ] и [ c, b ]:
8.Определенный интеграл от неотрицательной функции всегда больше или равен нулю:
9.Определенный интеграл от неположительной функции всегда меньше или равен нулю:
10. Формула Ньютона-Лейбница
11. Метод подстановки для определенного интеграла
12. Интегрирование по частям
|

 ,
,  .
.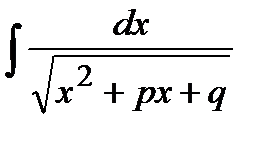 ,
,  .
.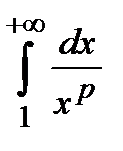 .
.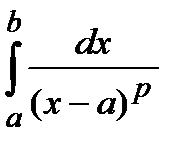 .
. 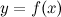
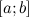 ;
; ;
;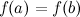 .
.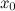 , в которой
, в которой 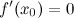 .
. , то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.
, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.
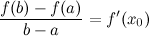
 и
и  найдется точка
найдется точка 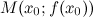 , такая, что через эту точку можно провести касательную, параллельную хорде
, такая, что через эту точку можно провести касательную, параллельную хорде  (рис. 1).
(рис. 1).
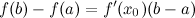
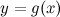 :
: на интервале
на интервале 
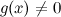 и
и 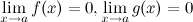 ;
;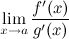 существует конечный или бесконечный.
существует конечный или бесконечный.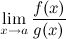 , причем
, причем 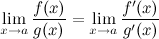
 при
при 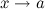 .
.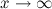 . Чтобы убедится в этом, достаточно сделать замену
. Чтобы убедится в этом, достаточно сделать замену  и воспользоваться результатом выше приведенной теоремы.
и воспользоваться результатом выше приведенной теоремы.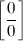 и
и 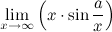

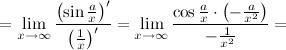


 либо равна нулю, либо не существует.
либо равна нулю, либо не существует.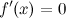 , называются стационарными точками функции.
, называются стационарными точками функции.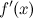 не существует.
не существует. , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех  из этой окрестности выполняется неравенство:
из этой окрестности выполняется неравенство:  .
. .
.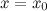 функция
функция 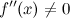 в точке
в точке  , то в точке
, то в точке 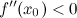 , то в точке
, то в точке 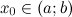 вторую производную. Тогда, если
вторую производную. Тогда, если 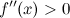 всюду на интервале
всюду на интервале 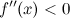 , то функция имеет выпуклость.
, то функция имеет выпуклость.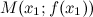 , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости.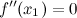 или не существует.
или не существует. ;
;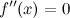 или не существует в точке
или не существует в точке 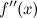 при переходе через точку
при переходе через точку 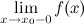 или
или 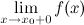 равно
равно 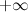 или
или  .
.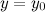 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 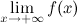 или
или 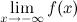 равно
равно 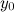 .
.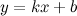 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 
 и
и  , то функция имеет наклонную асимптоту
, то функция имеет наклонную асимптоту 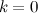 .
.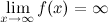 , то функция может иметь наклонную асимптоту.
, то функция может иметь наклонную асимптоту.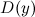 и область допустимых значений
и область допустимых значений 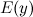 функции.
функции. и построить ее график.
и построить ее график.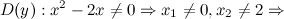

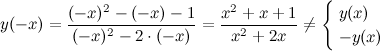
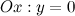 :
: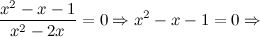
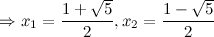

 : в данной точке функция неопределенна.
: в данной точке функция неопределенна.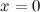 и
и 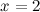 - вертикальные асимптоты.
- вертикальные асимптоты.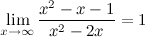
 - горизонтальная асимптота.
- горизонтальная асимптота.
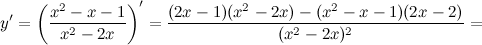
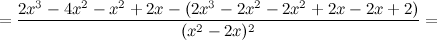
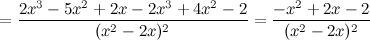
 для любого
для любого 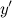 не существует при
не существует при 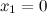 и
и 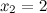 .
.
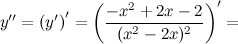
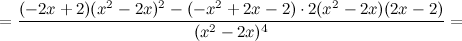
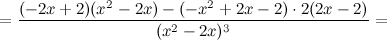
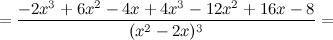

 ; при
; при 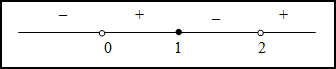
 и
и 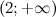 функция вогнута, а на промежутках
функция вогнута, а на промежутках 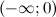 и
и 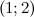 - выпукла. Так как при переходе через точку
- выпукла. Так как при переходе через точку  вторая производная поменяла знак, то эта точка является точкой перегиба.
вторая производная поменяла знак, то эта точка является точкой перегиба.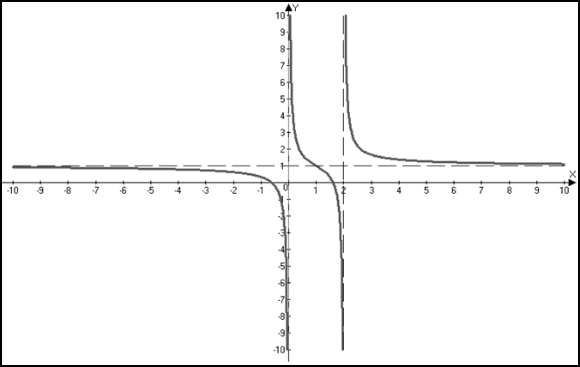
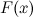 называется первообразной для функции
называется первообразной для функции 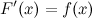
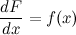 или
или 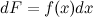
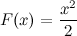 является первообразной для функции
является первообразной для функции 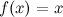 , так как
, так как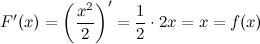
 , где
, где 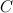 - произвольная постоянная, также будет первообразной для функции
- произвольная постоянная, также будет первообразной для функции 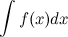 . То есть
. То есть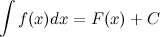
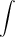 называется интегралом,
называется интегралом, 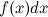 - подынтегральным выражением,
- подынтегральным выражением, 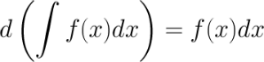

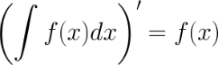
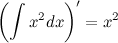

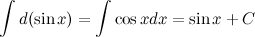

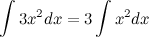
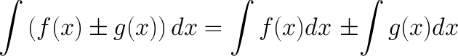
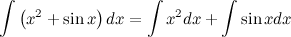
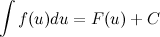 , где функция
, где функция  - произвольная функция с непрерывной производной.
- произвольная функция с непрерывной производной.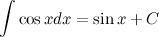 , а тогда
, а тогда

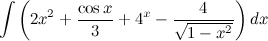

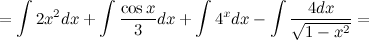

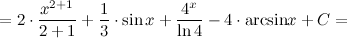
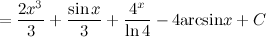
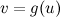 такие, что
такие, что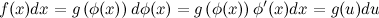
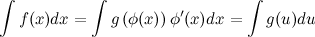


 называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, т.е.
называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, т.е. 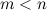 . Если же
. Если же 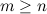 , то дробь называется неправильной.
, то дробь называется неправильной. является правильной.
является правильной. и
и  - неправильные рациональные дроби.
- неправильные рациональные дроби.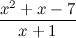 в виде суммы многочлена и правильной дроби.
в виде суммы многочлена и правильной дроби.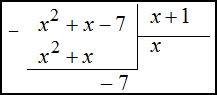
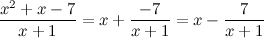


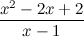 является неправильной рациональной дробью (так как степень числителя больше степени знаменателя), то выделим целую часть, для этого числитель поделим на знаменатель в столбик:
является неправильной рациональной дробью (так как степень числителя больше степени знаменателя), то выделим целую часть, для этого числитель поделим на знаменатель в столбик: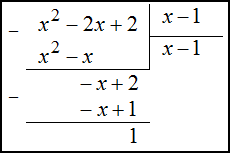


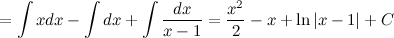
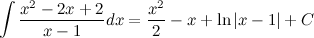
 ) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись
) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись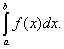
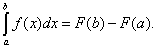 (38)
(38)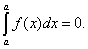

 (39)
(39) численно равен площади фигуры, ограниченной осью абсцисс, прямыми
численно равен площади фигуры, ограниченной осью абсцисс, прямыми  и
и 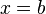 и графиком функции
и графиком функции 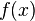 .
.