Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первое достаточное условие экстремумаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема (Первое достаточное условие экстремума) Пусть для функции 1. функция непрерывна в окрестности точки 2. 3. производная Тогда в точке Если производная Таким образом, для того чтобы исследовать функцию 1. найти производную 2. найти критические точки, то есть такие значения 3. исследовать знак производной слева и справа от каждой критической точки; 4. найти значение функции в экстремальных точках. Второе достаточное условие экстремума Теорема (Второе достаточное условие экстремума) Пусть для функции 1. она непрерывна в окрестности точки 2. первая производная 3. Тогда в точке Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше двух) Пусть функция 1. Если · если · если 2. Если Доказательство за счет теоремы брука тейлора.
8 Выпуклость функции, точки перегиба График функции График функции
Теоремы о выпуклости функции и точках перегиба Теорема (Об условиях выпуклости или вогнутости графика функции)
Пусть функция Определение Точкой перегиба графика функции Теорема (О необходимом условии существования точки перегиба) Если функция Теорема (О достаточном условии существования точки перегиба) Если: 1. первая производная 2. вторая производная 3. тогда в точке Схема исследования функции на выпуклость, вогнутость 1. Найти вторую производную функции. 2. Найти точки, в которых вторая производная равна нулю или не существует. 3. Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.
9 Асимптоты графика функции Виды асимптот Определение Прямая Замечание. Прямая Определение Прямая Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую. Определение Прямая Нахождение наклонной асимптоты Теорема (условиях существования наклонной асимптоты) Если для функции Замечание Горизонтальная асимптота является частным случаем наклонной при Замечание Если при нахождении горизонтальной асимптоты получается, что Замечание Кривая
10 Схема исследования и построения графика функции. При построении графика функции необходимо провести ее предварительное исследование. Примерная схема исследования функции с целью построения ее графика имеет следующую структуру: 1. Область определения 2. Четность, нечетность функции. 3. Точки пересечения с осями. 4. Асимптоты функции. 5. Экстремумы и интервалы монотонности. 6. Точки перегиба и промежутки выпуклости, вогнутости. 7. Сводная таблица. Замечание Схема представлена как примерная. Пункты исследования можно опускать, если они дают банальную информацию, или переставлять, если обнаруживаются интересные особенности поведения графика. Замечание Для уточнения графика можно найти некоторые дополнительные точки, но иногда удается обойтись и без них. Замечание Рекомендуется строить график одновременно с исследованием функции, нанося на координатную плоскость информацию по завершении каждого пункта исследования.
Задание. Исследовать функцию Решение. 1) Область определения функции.
2) Четность, нечетность.
Функция общего вида. 3) Точки пересечения с осями. а) с осью
то есть точки б) с осью 4) Асимптоты. а) вертикальные: прямые б) горизонтальные асимптоты:
то есть прямая в) наклонные асимптоты
Таким образом, наклонных асимптот нет. 5) Критические точки функции, интервалы возрастания, убывания.
Найдем точки, в которых первая производная равна нулю или не существует:
Таким образом, функция убывает на всей области существования. Точек экстремума нет. 6) Точки перегиба, интервалы выпуклости, вогнутости.
Найдем точки, в которых вторая производная равна нулю или не существует:
Таким образом, на промежутках 7) Эскиз графика.
11 Понятие первообразной функции и неопределенного интеграла. Первообразная, основные понятия и определения Определение Функция
Последнее равенство можно записать через дифференциалы:
Пример Функция
Первообразная Теорема (О бесконечном множестве первообразных для функции) Если функция Неопределенный интеграл Определение Совокупность всех первообразных функции
Знак
Операция нахождения первообразной или неопределенного интеграла от функции
12 Свойства неопределенного интеграла 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению
Пример
Больше примеров решений→ 2. Производная от неопределенного интеграла равна подынтегральной функции
Пример
Больше примеров решений→ 3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
Пример
Больше примеров решений→ 4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла
Пример
Больше примеров решений→ 5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций
Пример
Больше примеров решений→ 6. Если Пример Известно, что
13 Таблица основных интегралов
Метод непосредственного интегрирования Определение Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. Таким образом, алгоритм действий следующий: 1. тождественное преобразование подынтегральной функции; 2. применение свойств неопределенного интеграла: вынесение константы за знак интеграла, представление интеграла от суммы функций в вид суммы интегралов; 3. использование таблицы интегралов. В простейших примерах для применения непосредственного интегрирования достаточно разложить подынтегральную функцию на слагаемые и постоянные величины вынести за знак интеграла. При определенной практике интегрирования обычно эти действия проводят устно, записывая лишь результат интегрирования. Задание. Найти интеграл Решение. Воспользуемся свойствами интеграла и приведем данный интеграл к нескольким табличным.
14 Метод внесения новой переменной под знак дифференциала Пусть требуется найти неопределенный интеграл
Тогда
Указанное преобразование подынтегрального выражения называют подведением под знак дифференциала. Тогда, если
Замечание. При интегрировании методом подведения под знак дифференциала полезны следующие равенства для дифференциалов:
|
||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.175.197 (0.011 с.) |

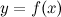 выполнены следующие условия:
выполнены следующие условия: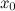 ;
;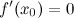 или
или  не существует;
не существует;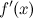 при переходе через точку
при переходе через точку 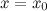 функция
функция  , в которых
, в которых 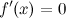 или
или 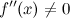 в точке
в точке  , то в точке
, то в точке 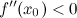 , то в точке
, то в точке 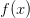 определена в некоторой окрестности точки
определена в некоторой окрестности точки 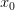 , и в этой точке существуют производные до n-го порядка пусть
, и в этой точке существуют производные до n-го порядка пусть 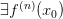 ,
, 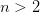 и
и 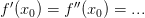
 ,
,  Тогда:
Тогда: (т.е
(т.е 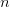 — четное), то
— четное), то 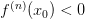 , то
, то  , то
, то 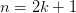 (т.е
(т.е  , является на этом интервале выпуклым, если график этой функции в пределах интервала
, является на этом интервале выпуклым, если график этой функции в пределах интервала 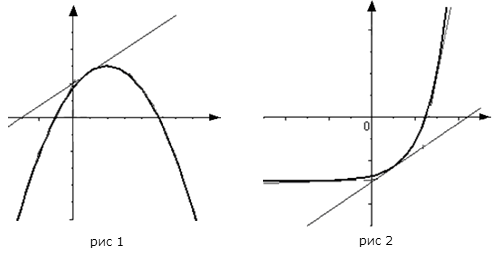
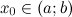 вторую производную. Тогда, если
вторую производную. Тогда, если 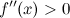 всюду на интервале
всюду на интервале 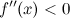 , то функция имеет выпуклость.
, то функция имеет выпуклость.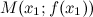 , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости.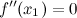 или не существует.
или не существует. ;
;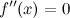 или не существует в точке
или не существует в точке 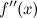 при переходе через точку
при переходе через точку 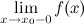 или
или 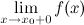 равно
равно 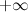 или
или  .
.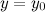 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 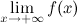 или
или 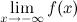 равно
равно 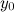 .
.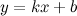 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 
 и
и  , то функция имеет наклонную асимптоту
, то функция имеет наклонную асимптоту 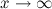 .
.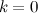 .
.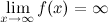 , то функция может иметь наклонную асимптоту.
, то функция может иметь наклонную асимптоту.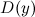 и область допустимых значений
и область допустимых значений 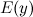 функции.
функции. и построить ее график.
и построить ее график.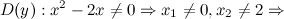

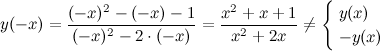
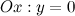 :
: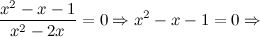
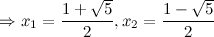

 : в данной точке функция неопределенна.
: в данной точке функция неопределенна.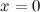 и
и 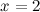 - вертикальные асимптоты.
- вертикальные асимптоты.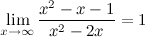
 - горизонтальная асимптота.
- горизонтальная асимптота.
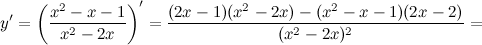
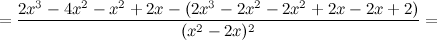
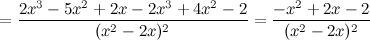
 для любого
для любого 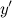 не существует при
не существует при 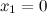 и
и 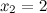 .
.
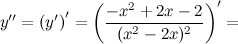
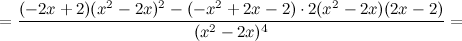
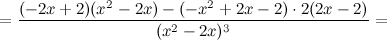
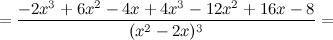

 ; при
; при 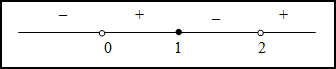
 и
и 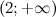 функция вогнута, а на промежутках
функция вогнута, а на промежутках 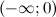 и
и  - выпукла. Так как при переходе через точку
- выпукла. Так как при переходе через точку  вторая производная поменяла знак, то эта точка является точкой перегиба.
вторая производная поменяла знак, то эта точка является точкой перегиба.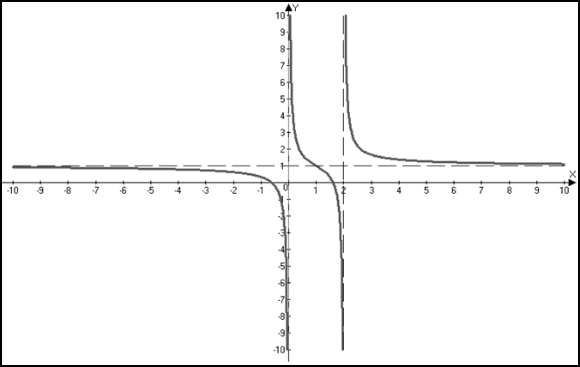
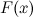 называется первообразной для функции
называется первообразной для функции 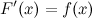
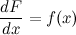 или
или 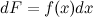
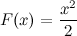 является первообразной для функции
является первообразной для функции 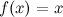 , так как
, так как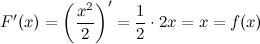
 , где
, где 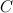 - произвольная постоянная, также будет первообразной для функции
- произвольная постоянная, также будет первообразной для функции  на рассматриваемом промежутке.
на рассматриваемом промежутке.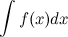 . То есть
. То есть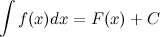
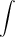 называется интегралом,
называется интегралом, 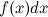 - подынтегральным выражением,
- подынтегральным выражением, 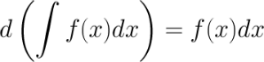

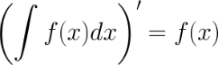
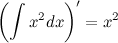

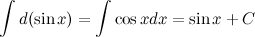

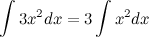
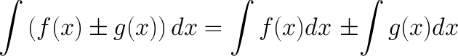
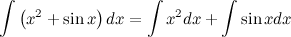
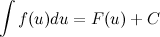 , где функция
, где функция  - произвольная функция с непрерывной производной.
- произвольная функция с непрерывной производной.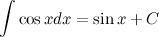 , а тогда
, а тогда

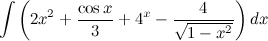

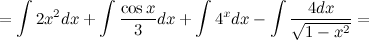

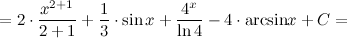
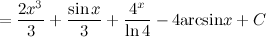
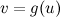 такие, что
такие, что