
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимые и достаточные условия экстремума функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определение 8.12. Пусть функция у=f (х) определена в некоторой окрестности точки х0. Точка х0 называется точкой максимума (минимума) функции f (х), если существует такое Теорема 8.14 (необходимое условие экстремума). Если функция f (х) определена в некоторой окрестности точки х0 и точка х0 является точкой экстремума функции f (х), то либо производная f' (х0) обращается в нуль, либо не существует. Простые примеры показывают, что эти необходимые условия экстремума не являются достаточными. Теорема 8.15 (первое достаточное условие экстремума). Пусть функция f (х) дифференцируема в окрестности точки а) если f' (х) > 0 при х < х0 и f'( х) < 0 при х > х0, то х0 — точка строгого максимума; б) если f' (х) < 0 при х < х0 и f '(х) > 0 при х > х0, то х0 — точка строгого минимума; в) если f' (х) в окрестности точки х0 не меняет знак, то экстремума нет. Коротко можно сказать, что если производная f' (х) при переходе через точку х 0 меняет знак с плюса на минус, то х 0 - точка строгого максимума, а если с минуса на плюс, то х 0 - точка строго минимума. Заметим сразу же, что эти условия, являясь достаточными, не являются необходимыми для экстремума. Иногда вызывает затруднение исследование знака первой производной в окрестности заданной точки. В ряде случаев бывает удобным применить при изучении точек экстремума следующую теорему. Теорема 8.16 (второе достаточное условие экстремума). Пусть в точке х0 для функции f (х) выполняются условия: f' (х0) = 0,
Выпуклость и вогнутость графика функции. Точка перегиба Определение. График функции у=f(x), дифференцируемой на интервале (а;b), имеет на этом интервале выпуклость, направленную вверх (вниз), если график этой функции в пределах интервала (а;b) лежит не выше (не ниже) любой своей касательной. Теорема (об условиях выпуклости вверх или вниз). Пусть функция y = f (x) определена на интервале (a; b) и имеет непрерывную, не равную нулю в точке x0 ∈ (a;b) 0 вторую производную. Тогда, если f '' (x) > 0 всюду на интервале (a; b), то функция имеет выпуклость вниз на этом интервале, если f ‘’ (x) < 0, то функция выпукла вверх. Определение. Точкой перегиба графика функции y=f(x) называется точка M (x1,f(x1)), разделяющая промежутки выпуклости вверх и вниз. Иными словами, точка M (x1,f(x1)) - точка перегиба кривой, если в этой точке кривая переходит с одной стороныкасательной на другую, меняя направление выпуклости. Теорема (о необходимом условии точки перегиба). Если M (x 1,f(x1)) есть точка перегиба дважды дифференцируемой функции y = f (x), то f ‘’ (x1) =0 или f '' (x1) = ∞. теорема (о достаточном условии точки перегиба). Если вторая производная f ‘’(x) дважды дифференцируемой функции при переходе через некоторую точку x1 меняет знак, причем f ‘’ (x1) =0, то точка M(x1,f(x1)) есть точка перегиба кривой y = f (x). Схема исследования функции на выпуклость 1) Найти вторую производную функции; 2) найти точки, в которых вторая производная равна нулю или обращается в бесконечность; 3) исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба; 4) найти значения функции в точках перегиба.
Асимптоты графика функции Прямая x = x 0 называется вертикальной асимптотой графика функции y=f(x), если хотя бы одно из предельных значений lim x → x −0 f(x) или lim x → x +0 f(x) равно + ∞ или − ∞. Прямая y = y0 называется горизонтальной асимптотой графика функции y=f(x), если хотя бы одно из предельных значений lim x →+∞ f (x)или lim x →-∞ f (x)равно b. График функции может иметь только правую горизонтальную асимптоту или только левую. Прямая y = kx + b называется наклонной асимптотой графика функции y=f(x), если lim x →+∞(f(x)-kx-b)= 0, т.е. когда функция при x →∞ представима в виде f (x) = kx + b +α(x), где lim x →+∞α(x) = 0. Существование асимптоты y = kx + b у кривой y=f(x) при x →∞ означает, что при x →∞ функция ведет себя «почти как линейная», т. е. отличается от линейной функции y = kx + b бесконечно мало. Наклонная асимптота может быть как правой так и левой. Теорема (об условиях существования наклонной асимптоты) Если для функции y = f (x) существуют пределы lim x →∞
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 , что для всех
, что для всех  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 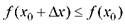
 . Если существует такое
. Если существует такое  ,
, 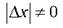 , что для всех
, что для всех  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 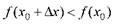
 , то точка х0 называется точкой строгого максимума (минимума). Точки максимума и минимума называются точками экстремума.
, то точка х0 называется точкой строгого максимума (минимума). Точки максимума и минимума называются точками экстремума. , за исключением может быть самой точки х 0, в которой она является непрерывной. Тогда:
, за исключением может быть самой точки х 0, в которой она является непрерывной. Тогда: . Тогда, если f''( х0) > 0, то f (х) имеет в точке х0 строгий минимум; если f "(х0) < 0, то f (х) имеет в точке х0 строгий максимум.
. Тогда, если f''( х0) > 0, то f (х) имеет в точке х0 строгий минимум; если f "(х0) < 0, то f (х) имеет в точке х0 строгий максимум. и lim x →∞
и lim x →∞  , то функция имеет наклонную асимптоту y = kx + b при x →∞.
, то функция имеет наклонную асимптоту y = kx + b при x →∞.


