
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства вещественных чиселСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Сложение и умножение вещественных чисел. Для любой пары a и b вещественных чисел определены единственным образом два вещественных числа a+b и a·b, называемые соответственно их суммой и произведением. Для любых вещественных чисел a, b, c выполняются следующие свойства: 1) a + b = b + a (переместительное свойство сложения); 2) a + (b + c) = (a + b) + c (сочетательное свойство сложения); 3) a · b = b · a (переместительное свойство умножения); 4) a · (b ·c) = (a · b) · c (сочетательное свойство умножения); 5) (a + b) · c = a · c + b · c (распределительное свойство); 6) существует единственное число 0 такое, что a + 0 = 0 + a = a для любого числа a; 7) для любого числа a существует число (- a) такое, что a + (- a) = 0; 8) существует единственное число 1 ¹ 0 такое, что для любого числа a имеет место равенство a · 1 = a; 9) для любого числа a ¹ 0 существует такое число a-1, что a · a-1 =1, число a-1 обозначается также символом Сравнение вещественных чисел. Для любых двух вещественных чисел a и b установлено одно из соотношений: a = b (a равно b), a > b (a больше b) или a < b. Каковы бы ни были числа a, b, c, выполняются соотношения: 1) если a = b и b = с, то a = с; 2) если a > b и b > с, то a > с; 3) если a > b, то a + c > b + c; 4) если a > 0, b > 0, то a · b > 0. Непрерывность вещественных чисел. Пусть X и Y ─ два множества, состоящих из вещественных чисел. Тогда, если для любых чисел xÎ X и yÎY выполняется неравенство x ≤ y, то существует хотя бы одно число с такое, что для всех таких x и y выполняются неравенства x ≤ с ≤ y. Свойством непрерывности обладает множество всех вещественных чисел. Однако множество только рациональных чисел таким свойством не обладает. Теорема. Множество Доказательство. Доказывать будем «методом от противного». Пусть Рассмотрим еще несколько свойств вещественных чисел, которые вытекают из сказанного. Для любых вещественных чисел a, b, c, d: 1. Число x = b + (- a) является решением уравнения a + x = b. Доказательство. Определение. Число b + (- a) называется разностью чисел b и a и обозначается b – a. 2. Если b > a, то b – a > 0. Доказательство. 3. Число x = b · a-1 является решением уравнения a · x = b, если a ¹ 0. Доказательство. Определение. Число b · a-1 называется частным чисел b и a и обозначается 4. Если a < b, то – a > - b. Доказательство. Так как 5. Если a > b, c > d, то a + c > b + d. Доказательство. 6. Если a < b, c > d, то a – c <b – d. Это свойство доказывается с использованием свойств 4 и 5. 7. a – a = 0. Доказательство. 8. – Доказательство. 9. a · 0 = 0. Доказательство. 10. (- a)b = - ab. Доказательство. Абсолютная величина числа
Определение. Абсолютной величиной ( или модулем) числа х называется само число Абсолютная величина числа Из определения абсолютной величины числа вытекает ряд ее свойств. 1. 2. 3. Теорема 1. Пусть Доказательство. Пусть Пусть Теорема 2. Абсолютная величина суммы двух чисел не больше суммы абсолютных величин этих чисел, т. е. Доказательство. Пусть Из этой теоремы следует, что абсолютная величина разности двух чисел не больше суммы абсолютных величин этих чисел, т. е. Теорема 3. Абсолютная величина разности двух чисел не меньше разности абсолютных величин этих чисел, т. е. Доказательство. Для любых чисел Аналогично доказывается утверждение о том, что абсолютная величина суммы двух чисел не меньше разности абсолютных величин этих чисел, т. е. Замечание. Для любых чисел х и у имеют место легко проверяемые соотношения
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.92.56 (0.006 с.) |

 .
. рациональных чисел не является непрерывным.
рациональных чисел не является непрерывным. ,
,  .Тогда для
.Тогда для  ,
,  выполняется неравенство
выполняется неравенство  , поэтому
, поэтому  такое, что
такое, что  . Однако таким числом может быть только число
. Однако таким числом может быть только число  , которое не является рациональным. Пришли к противоречию. Теорема доказана.
, которое не является рациональным. Пришли к противоречию. Теорема доказана. .
. , тогда
, тогда  или
или  .
. .
. , или b: a.
, или b: a. , то
, то  , следовательно,
, следовательно,  .
. , тогда
, тогда 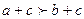 .
.  , следовательно,
, следовательно,  . Таким образом,
. Таким образом,  .
. .
. a)
a)  = a.
= a. .
. .
. .
. , если
, если  , число (-
, число (-  .
. . Таким образом,
. Таким образом,  , если
, если  , если
, если  . Доказательство. Если
. Доказательство. Если  , то
, то  . Если
. Если  , то
, то  , но
, но  , т. е.
, т. е.  .
. . Доказательство. Если
. Доказательство. Если  и тогда
и тогда  . Если
. Если  .
. . Доказательство. Если
. Доказательство. Если  ,
,  , т. е.
, т. е.  . Если
. Если  . Так как
. Так как  , или
, или  , откуда
, откуда  , т. е.
, т. е.  . Поэтому
. Поэтому  |. Получаем, что
|. Получаем, что  положительное число. Тогда неравенства
положительное число. Тогда неравенства  и
и  равносильны. ((" e, e > 0: |х| £ e) Û (- e £ х £ e)).
равносильны. ((" e, e > 0: |х| £ e) Û (- e £ х £ e)). , таким образом,
, таким образом,  . Если
. Если  , откуда
, откуда  . Объединяя неравенства
. Объединяя неравенства  ,
, 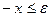 . По определению,
. По определению,  , поэтому
, поэтому  .
. – произвольные числа. По свойству 3 для них выполняются неравенства:
– произвольные числа. По свойству 3 для них выполняются неравенства:  ,
,  . Поэтому, складывая эти неравенства, получаем
. Поэтому, складывая эти неравенства, получаем  . По предыдущей теореме это равносильно неравенству
. По предыдущей теореме это равносильно неравенству  .
. .
. . По предыдущей теореме
. По предыдущей теореме  . Поэтому
. Поэтому  .
. и
и  , если
, если  . Эти соотношения предлагается доказать самостоятельно.
. Эти соотношения предлагается доказать самостоятельно.


