
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наиболее употребляемые числовые множестваСодержание книги Поиск на нашем сайте
Пусть а и b – два числа, причем a < b. Будем пользоваться следующими обозначениями: 1) [a, b] = {x | a £ x £ b} − отрезок (сегмент); 2) (a, b] = {x | a < x £ b} − полуинтервал; 3) [a, b) = {x | a £ x <b} − полуинтервал; 4) (a, b) = {x | a < x < b} − интервал; 5) [a, +¥) = {x | a £ x} − полуинтервал; 6) (a, +¥) = {x | a < x} − интервал; 7) (- ¥, b] = {x | x £ b} − полуинтервал; 8) (- ¥,, b) = {x | x < b} − интервал. Множество всех вещественных чисел обозначается интервалом (- ¥, + ¥) или { x | - ¥ < x < + ¥}. Промежутки [a, b], (a, b], [a, b), (a, b) называются конечными, a и b − их концами. Остальные промежутки называются бесконечными. Числовым промежуткам соответствуют промежутки на координатной прямой. Например, сегмент [ х1, х2 ] изображается на координатной прямой отрезком М1М2 таким, что точка М1 имеет координату х1, а точка М2 – координату х2. Изображением множества Определение. Пусть a – произвольная точка числовой прямой, d − положительное вещественное число. Интервал
Прямоугольная система координат на плоскости
Две взаимно перпендикулярные оси Ох и Оу, имеющие общее начало О и одинаковую масштабную единицу, образуют прямоугольную систему координат на плоскости.
Ось Ох называется осью абсцисс, ось Оу – осью ординат. Точка О пересечения осей называется началом координат. Плоскость, в которой расположены оси Ох и Оу, называется координатной плоскостью и обозначается Ох у. Пусть М – произвольная точка плоскости. Опустим из этой точки перпендикуляры Мх и Му на оси Ох и О у соответственно. Определение. Декартовыми прямоугольными координатами (или прямоугольными координатами) х и у точки М называются величины ОМх и ОМу направленных отрезков Декартовы координаты х и у точки М называются соответственно ее абсциссой и ординатой. То, что точка М имеет координаты х и у, символически обозначают так: М (х, у). Координатные оси разбивают плоскость на четыре части, которые называются четвертями, квадрантами или координатными углами. Квадранты нумеруются римскими цифрами I, II, III, IV. В зависимости от расположения точек в той или иной четверти определяются и знаки их координат.
Полярная система координат
Определение. Полярными координатами точки М называются двачисла r и j, первое из которых (полярный радиус r) равно расстоянию точки М от полюса О, а второе (полярный угол j) - угол, на который надо повернуть против часовой стрелки луч Ох до совмещения с лучом ОМ. При этом предполагается, что точка М не совпадает с полюсом. Для полюса О полярный радиус r равен нулю, а полярный угол j не определен, т. е. ему можно присвоить любое значение. Точку плоскости М с полярными координатами r и j обозначают символом М (r, j). Для того чтобы соответствие между отличными от полюса точками плоскости и парами полярных координат (r, j) было взаимно однозначным, обычно считают, что 0 £ r < + ¥, 0 £ j < 2p. Однако в некоторых случаях приходится рассматривать углы, большие 2p, а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по часовой стрелке. Установим связь между полярными и прямоугольными координатами одной и той же точки плоскости. Будем предполагать, что начало прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка М имеет полярные координаты r и j и прямоугольные координаты х и у. Тогда
Формулы (1.1) выражают прямоугольные координаты через полярные. Выражения полярных координат точки через прямоугольные следуют из формул (1.1):
Вторая из этих формул определяет два значения полярного угла, так как j изменяется от 0 до 2p. Из этих двух значений выбирается то, при котором удовлетворяются равенства (1.1), т. е. нужно, используя знаки х и у, определить квадрант, в котором находится точка М. Когда х = 0, tg j не может быть вычислен по формулам (1.2). В этом случае Для простоты нахождения полярного угла j через прямоугольные координаты можно воспользоваться следующей таблицей:
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.50.170 (0.006 с.) |

 всех чисел служит вся координатная прямая. Поэтому множество
всех чисел служит вся координатная прямая. Поэтому множество  называется d -окрестностью точки a.
называется d -окрестностью точки a.
 и
и  .
.
 Выберем на плоскости некоторую точку О (полюс) и некоторый выходящий из нее луч Ох и укажем единицу масштаба.
Выберем на плоскости некоторую точку О (полюс) и некоторый выходящий из нее луч Ох и укажем единицу масштаба.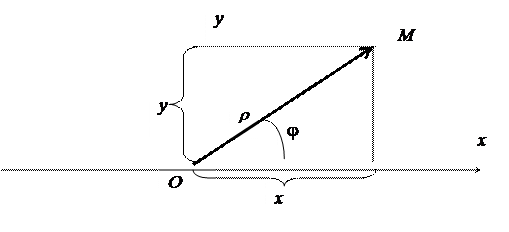
 . (1.1)
. (1.1) . (1.2)
. (1.2) (если у > 0) и
(если у > 0) и  (если у < 0).
(если у < 0).







