
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корни уравнения четвертой степениСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение четвертой степени
Следовательно, должно выполняться условие Это уравнение третьей степени относительно
где
Решение последнего уравнения сводится к решению двух квадратных уравнений. П р и м е р. Решить уравнение Решение. Введем дополнительный параметр
Рассмотрим уравнение
При решении этого уравнения получаем, что один из его корней
Из полученных соотношений находим корни исходного уравнения: Индивидуальные задания по теме «Комплексные числа» ВАРИАНТ 1 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих неравенству 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество:
ВАРИАНТ 2 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 3 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 4 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 5 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество ВАРИАНТ 6 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 7 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 8 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 9 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 10 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество ВАРИАНТ 11 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 12 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 13 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 14 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 15 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 16 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 17 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 18 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 19 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
ВАРИАНТ 20 1. Найти действительную и мнимую части комплексного числа 2. Найти модуль и главное значение аргумента ( 3. Найти все значения корней и построить их на комплексной плоскости 4. Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам 5. Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке (-p; p]) 6. Доказать тождество
Индивидуальные задания по теме «Многочлены»
ВАРИАНТ 1 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 2 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 2 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 3 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 3 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 3 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 5 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня -1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 6 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 2 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 7 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 8 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 9 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня -1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 10 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 11 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 2 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 12 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня -1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 13 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 3 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 14 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня -1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 15 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 2 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 16 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня -1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 17 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 18 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня -1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 19 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 1 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
ВАРИАНТ 20 1. Найти остаток от деления многочлена 2. Пользуясь схемой Горнера, разложить на простейшие дроби выражение 3. Чему равен показатель кратности корня 2 для многочлена 4. Найти наибольший общий делитель 5. Найти корни уравнения
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 (2.4) решается методом Феррари. Преобразуем левую часть (2.4) с помощью вспомогательного параметра
(2.4) решается методом Феррари. Преобразуем левую часть (2.4) с помощью вспомогательного параметра  следующим образом:
следующим образом:
 . (2.5) Параметр
. (2.5) Параметр  .
. − один из корней этого уравнения. Тогда выражение
− один из корней этого уравнения. Тогда выражение  приводится к виду:
приводится к виду: ,
, ,
, 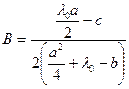 , а уравнение (2.4) принимает вид
, а уравнение (2.4) принимает вид или
или .
. .
.
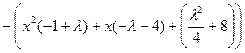 .
. . Это уравнение имеет один кратный корень, если
. Это уравнение имеет один кратный корень, если 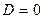 , т. е. выполняется равенство
, т. е. выполняется равенство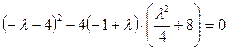 .
. . При этом значении
. При этом значении  , т. е.
, т. е.  .
. ,
,  .
. .
. ) комплексного числа
) комплексного числа  .
. .
.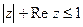 .
. .
. .
. .
. .
. .
. ,
,  .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.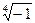 .
. .
. .
. .
. .
.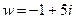 .
. .
. ,
,  .
. .
. .
. .
. .
. .
.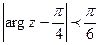 .
. .
. .
. .
.
 .
. .
. .
.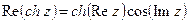 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. ,
,  .
. .
. .
. .
.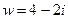 .
. .
. ,
, 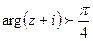 .
. .
. ,
,  .
. .
.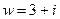 .
. .
. .
. .
.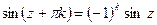 ,
,  .
. .
. .
. ,
,  .
. .
. .
. .
.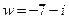 .
. .
. ,
,  .
. .
. ,
,  .
. .
. .
. ,
,  .
. .
. .
. .
. .
. ,
,  .
. .
. .
. .
. .
. .
. ,
,  .
. .
. .
. .
. .
. .
.
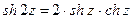 .
. .
.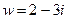 .
. .
. ,
, 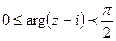 .
. .
. .
. .
. .
. .
. ,
,  .
. .
. .
.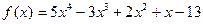 на многочлен
на многочлен  .
. .
. ?
? многочленов
многочленов  и
и  .
. .
.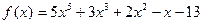 на многочлен
на многочлен  .
.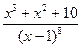 .
.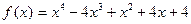 ?
? и
и 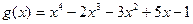 .
. .
. на многочлен
на многочлен  .
. .
. ?
? и
и  .
. .
. на многочлен
на многочлен 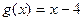 .
. .
.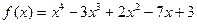 ?
?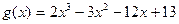 .
. .
. на многочлен
на многочлен  .
. .
. ?
? .
. .
. на многочлен
на многочлен  .
. ?
? .
. .
. на многочлен
на многочлен  .
.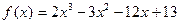 ?
? .
. на многочлен
на многочлен 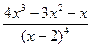 .
. ?
? .
. .
. на многочлен
на многочлен  .
. ?
? .
. .
. на многочлен
на многочлен  .
. ?
?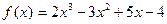 и
и  .
. .
. на многочлен
на многочлен 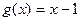 .
. .
. .
. ?
? и
и  .
. на многочлен
на многочлен 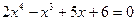 .
. .
. ?
?


