
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наибольший общий делитель двух многочленов.Содержание книги Поиск на нашем сайте
Алгоритм Евклида
Определение. Наибольшим общим делителем (НОД) двух отличных от нуля многочленов Обозначается наибольший общий делитель многочленов Находить наибольший общий делитель двух многочленов можно с помощью алгоритма Евклида, который состоит в следующем. Выполним цепочку делений с остатком: Процесс конечен, т. е. на некотором шагу деление выполнится без остатка, потому что степень каждого последующего остатка меньше степени предыдущего. Остаток Наибольший общий делитель двух многочленов определяется с точностью до постоянного множителя. Поэтому, чтобы избежать дробных коэффициентов, можно умножать или сокращать делитель на любое не равное нулю число, причем не только начиная какое-либо из последовательных делений, но и в процессе этого деления. Это приведет к искажению частного, но интересующие нас остатки будут приобретать лишь множители нулевой степени, что допускается при отыскании НОД. П р и м е р. Найти наибольший общий делитель для многочленов Решение. Обозначим
С точностью до постоянного множителя остаток
Получили, что Наибольший общий делитель П р и м е р. Для многочленов Решение. В предыдущем примере нашли, что П р и м е р. Найти многочлены Решение. Найдем
Получили
То есть
Получили, что Свойства делимости многочленов 1. Если Доказательство. Так как 2. Если 3. Если 4. Если 5. Любой многочлен Доказательство. Пусть С, С ¹ 0 – многочлен нулевой степени. Тогда 6. Если 7. Если Доказательство. Многочлен 8. Многочлены 9. Если Доказательство. Пусть многочлен
Взаимно простые многочлены
Определение. Два многочлена называются взаимно простыми, если их нормализованный наибольший общий делитель равен 1, т. е. эти многочлены не имеют никаких общих делителей, кроме констант. Теорема. Для того чтобы многочлены Доказательство. Если
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 4641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.255.196 (0.01 с.) |

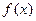 и
и  называется многочлен
называется многочлен  наибольшей степени среди многочленов, делящих оба многочлена
наибольшей степени среди многочленов, делящих оба многочлена  . Другими словами, наибольшим общим делителем двух отличных от нуля многочленов
. Другими словами, наибольшим общим делителем двух отличных от нуля многочленов  ,
,  ;
;  ,
,  ;
;  ,
,  ; …;
; …;  ,
,  ,
,  .
. и будет наибольшим общим делителем для многочленов
и будет наибольшим общим делителем для многочленов  .
. и
и  в кольце вещественных чисел.
в кольце вещественных чисел. ,
, 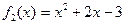 . Найдем остаток
. Найдем остаток  :
: . Найдем остаток
. Найдем остаток  . Для этого многочлен
. Для этого многочлен  разделим на
разделим на  , следовательно, для многочленов
, следовательно, для многочленов  и
и  наибольшим общим делителем является
наибольшим общим делителем является  , где
, где  и
и  − некоторые многочлены. Можно считать при этом, что если степени многочленов
− некоторые многочлены. Можно считать при этом, что если степени многочленов  ,
,  ,
,  , …,
, …,  ,
,  . Получили, что
. Получили, что  . Возвращаясь назад, придем к доказываемому равенству.
. Возвращаясь назад, придем к доказываемому равенству. и
и  найти такие многочлены
найти такие многочлены  и
и 
 .
. . Используя обратный ход в алгоритме Евклида, получим
. Используя обратный ход в алгоритме Евклида, получим 
 . После раскрытия скобок получим
. После раскрытия скобок получим  ,
,  .
. и
и  .
.


 ,
,  ,
,  . Далее
. Далее  .
.




 . С другой стороны,
. С другой стороны,  . Далее
. Далее  .
.


 , т. е.
, т. е.  . Учитывая, что
. Учитывая, что 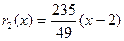 , получим
, получим 
 , т. е.
, т. е.  ,
,  .
. , то
, то  и
и  такие, что
такие, что  и
и  . Поэтому
. Поэтому  , т. е.
, т. е.  делится на
делится на  , то
, то  произведение
произведение  делится на
делится на  ,
,  делится на
делится на  ,
,  делится на
делится на  , т. е.
, т. е.  , где
, где  . Это свойство предлагается доказать самостоятельно.
. Это свойство предлагается доказать самостоятельно. ,
,  − делители многочлена
− делители многочлена  . Из того, что
. Из того, что  , следует доказываемое утверждение.
, следует доказываемое утверждение. ,
,  . Это свойство предлагается доказать самостоятельно.
. Это свойство предлагается доказать самостоятельно. , т. е.
, т. е.  и
и  , т. е.
, т. е.  и
и  и
и  такие, что
такие, что 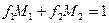 .
. .
.


