
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическое изображение вещественных чиселСодержание книги Поиск на нашем сайте
Рассмотрим произвольную прямую. На ней можно указать два противоположных направления. Выберем одно из направлений и масштабную единицу для измерения длин отрезков.
Определение. Прямая с выбранным на ней направлением называется осью. Рассмотрим на оси две произвольные точки А и В. Определение. Отрезок с граничными точками А и В называется направленным, если указано, какая из этих точек считается началом, а какая – концом отрезка. Направленный отрезок с началом в точке А и концом в точке В обозначим Для направленных отрезков, лежащих на оси (или на параллельных осях), вводится понятие величины направленного отрезка. Определение. Величиной АВ направленного отрезка Величины направленных отрезков Если точки А и В совпадают, то величина направленного отрезка Определение. Два ненулевых направленных отрезка называются равными, если при совмещении начал этих отрезков совпадают и их концы. Любые два нулевых направленных отрезка считаются равными. Над направленными отрезками определены следующие операции - операция сложения и умножения на число.
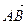 и и 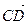 называется направленный отрезок называется направленный отрезок  , полученный при совмещении начала , полученный при совмещении начала  отрезка отрезка 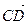 с концом с концом  отрезка отрезка 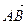 . .
Теорема. Величина суммы направленных отрезков равна сумме величин слагаемых отрезков. Доказательство. Пусть хотя бы один из отрезков Основное тождество. Для любых трех точек А, В, С, расположенных на оси, величины направленных отрезков Это тождество следует из доказанной выше теоремы. Определение. Произведением направленного отрезка Рассмотрим произвольную прямую, на которой выбрано направление и некоторая точка О, называемая началом координат. Определение. Прямая с выбранным направлением, масштабной единицей и началом координат называется координатной осью. Пусть М – произвольная точка на выбранной прямой.
Точке М поставим в соответствие число х, равное величине ОМ направленного отрезка Таким образом, каждой точке координатной прямой соответствует определенное вещественное число – ее координата. Верно и обратное утверждение: любому вещественному числу х соответствует некоторая точка М на координатной прямой, координата которой равна х. Следовательно, вещественные числа можно изображать точками на координатной прямой. Поэтому около точки на координатной прямой часто указывают число – ее координату.
Пусть точка М1 имеет координату х1, а точка М2 – координату х2.
Выразим величину М1М2 направленного отрезка
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.167 (0.009 с.) |



 или
или  .
. , если эти направления противоположны.
, если эти направления противоположны. при любом направлении оси отличаются знаками.
при любом направлении оси отличаются знаками.
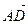 равна сумме длин отрезков
равна сумме длин отрезков  . Рассмотрим случай, когда отрезки
. Рассмотрим случай, когда отрезки  . Направление отрезка
. Направление отрезка  , т. е. справедливо равенство
, т. е. справедливо равенство  и
и 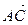 удовлетворяют соотношению
удовлетворяют соотношению  .
. , длина которого равна произведению числа
, длина которого равна произведению числа  на длину отрезка
на длину отрезка  и противоположно направлению
и противоположно направлению  .
.
 . Число х называется координатой точки М.
. Число х называется координатой точки М.

 через координаты точек М1 и М2. Согласно основному тождеству ОМ1 + М1М2 = ОМ2. Тогда М1М2 = ОМ2 - ОМ1, но ОМ1 = х1, ОМ2 = х2, поэтому М1М2 = х2 – х1.
через координаты точек М1 и М2. Согласно основному тождеству ОМ1 + М1М2 = ОМ2. Тогда М1М2 = ОМ2 - ОМ1, но ОМ1 = х1, ОМ2 = х2, поэтому М1М2 = х2 – х1.


