
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вещественные и комплексные числаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ВЕЩЕСТВЕННЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА Множества. Обозначения. Логические символы Понятие множества является одним из основных в математике. Слова «совокупность», «семейство», «система», «набор» и т. д. – синонимы слова «множество». Множество может содержать конечное (количество студентов в аудитории) или бесконечное (количество точек на прямой) число произвольных объектов. Определение. Объекты, из которых состоит множество, называютсяего элементами, или точками. Множества часто обозначают большими буквами, а его элементы – маленькими. Если Пусть даны два множества В математике часто используется пустое множество. Оно не содержит ни одного элемента и обозначается символом Æ. Пустое множество является подмножеством любого множества. В математических предложениях повторяются отдельные слова и целые выражения. Поэтому для их записи используется логическая символика. Рассмотрим несколько самых простых и наиболее употребляемых логических символов. Вместо слова «существует» или «найдется» используют символ $ (перевернутая латинская буква Е от английского слова Existence – «существование»), а вместо слов «любой», «каждый», «всякий» ─ символ " (перевернутое латинское А от английского слова Any ─ любой). Например, запись Для облегчения понимания и чтения утверждений, записанных с помощью логических символов, все, что относится только к каждому из них, заключается в круглые скобки. Например, запись
читается так: «для любого
Вещественные числа и их основные свойства
Известно, что множество вещественных чисел состоит из множества рациональных и множества иррациональных чисел. Определение. Рациональным называется число, которое можно представить в виде p/q, где p и q – целые числа, причем q ¹ 0. Определение. Всякое вещественное число, которое не является рациональным, называется иррациональным. Любое рациональное число является либо целым, либо представляется конечной или периодической бесконечной десятичной дробью ( Абсолютная величина числа
Определение. Абсолютной величиной ( или модулем) числа х называется само число Абсолютная величина числа Из определения абсолютной величины числа вытекает ряд ее свойств. 1. 2. 3. Теорема 1. Пусть Доказательство. Пусть Пусть Теорема 2. Абсолютная величина суммы двух чисел не больше суммы абсолютных величин этих чисел, т. е. Доказательство. Пусть Из этой теоремы следует, что абсолютная величина разности двух чисел не больше суммы абсолютных величин этих чисел, т. е. Теорема 3. Абсолютная величина разности двух чисел не меньше разности абсолютных величин этих чисел, т. е. Доказательство. Для любых чисел Аналогично доказывается утверждение о том, что абсолютная величина суммы двух чисел не меньше разности абсолютных величин этих чисел, т. е. Замечание. Для любых чисел х и у имеют место легко проверяемые соотношения
Полярная система координат
Определение. Полярными координатами точки М называются двачисла r и j, первое из которых (полярный радиус r) равно расстоянию точки М от полюса О, а второе (полярный угол j) - угол, на который надо повернуть против часовой стрелки луч Ох до совмещения с лучом ОМ. При этом предполагается, что точка М не совпадает с полюсом. Для полюса О полярный радиус r равен нулю, а полярный угол j не определен, т. е. ему можно присвоить любое значение. Точку плоскости М с полярными координатами r и j обозначают символом М (r, j). Для того чтобы соответствие между отличными от полюса точками плоскости и парами полярных координат (r, j) было взаимно однозначным, обычно считают, что 0 £ r < + ¥, 0 £ j < 2p. Однако в некоторых случаях приходится рассматривать углы, большие 2p, а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по часовой стрелке. Установим связь между полярными и прямоугольными координатами одной и той же точки плоскости. Будем предполагать, что начало прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка М имеет полярные координаты r и j и прямоугольные координаты х и у. Тогда
Формулы (1.1) выражают прямоугольные координаты через полярные. Выражения полярных координат точки через прямоугольные следуют из формул (1.1):
Вторая из этих формул определяет два значения полярного угла, так как j изменяется от 0 до 2p. Из этих двух значений выбирается то, при котором удовлетворяются равенства (1.1), т. е. нужно, используя знаки х и у, определить квадрант, в котором находится точка М. Когда х = 0, tg j не может быть вычислен по формулам (1.2). В этом случае Для простоты нахождения полярного угла j через прямоугольные координаты можно воспользоваться следующей таблицей:
Показателем. Формула Муавра
Для доказательства следующей теоремы понадобится метод математической индукции. Метод математической индукции. Чтобы доказать, что некоторое утверждение верно для любого натурального числа п, начиная с некоторого п 0, достаточно доказать, что: а) это утверждение верно для п = п 0; б) если данное утверждение справедливо для некоторого натурального числа k ³ n o, то оно верно также и для следующего натурального числа k+ 1. П р и м е р. Применяя метод математической индукции, доказать, что Решение: а) проверим, что это утверждение справедливо при П р и м е р. Применяя метод математической индукции, доказать, что Решение: а) проверим, что это утверждение справедливо при Теорема. Произведение комплексных чисел
Доказательство. Доказательство проведем, используя метод математической индукции. Очевидно, что при
В частности, при перемножении n равных комплексных чисел
Если в формуле (1.8) положить
Формула (1.8) получена в предположении, что n – целое положительное число. Покажем, что она остается верной при n = 0 и при целом отрицательном n, считая, что для комплексных чисел, как и для вещественных, При n = 0 получаем верное равенство: МНОГОЧЛЕНЫ
Схема Горнера
Теорема. Пусть Доказательство. Будем искать
Теорема доказана. Более того, получен очень удобный способ вычисления коэффициентов П р и м е р. Найти неполное частное и остаток от деления многочлена Решение. Составим таблицу:
Таким образом, неполное частное П р и м е р. Пользуясь схемой Горнера, разложить на простейшие дроби выражение Решение. Разложим числитель
Таким образом,
Кратные корни
Определение. Если Теорема. Если число с является к -кратным корнем многочлена Доказательство. Пусть Следствие. Если число с является корнем для П р и м е р. Чему равен показатель кратности корня 2 для многочлена Решение. При Алгоритм Евклида
Определение. Наибольшим общим делителем (НОД) двух отличных от нуля многочленов Обозначается наибольший общий делитель многочленов Находить наибольший общий делитель двух многочленов можно с помощью алгоритма Евклида, который состоит в следующем. Выполним цепочку делений с остатком: Процесс конечен, т. е. на некотором шагу деление выполнится без остатка, потому что степень каждого последующего остатка меньше степени предыдущего. Остаток Наибольший общий делитель двух многочленов определяется с точностью до постоянного множителя. Поэтому, чтобы избежать дробных коэффициентов, можно умножать или сокращать делитель на любое не равное нулю число, причем не только начиная какое-либо из последовательных делений, но и в процессе этого деления. Это приведет к искажению частного, но интересующие нас остатки будут приобретать лишь множители нулевой степени, что допускается при отыскании НОД. П р и м е р. Найти наибольший общий делитель для многочленов Решение. Обозначим
С точностью до постоянного множителя остаток
Получили, что Наибольший общий делитель П р и м е р. Для многочленов Решение. В предыдущем примере нашли, что П р и м е р. Найти многочлены Решение. Найдем
Получили
То есть
Получили, что Взаимно простые многочлены
Определение. Два многочлена называются взаимно простыми, если их нормализованный наибольший общий делитель равен 1, т. е. эти многочлены не имеют никаких общих делителей, кроме констант. Теорема. Для того чтобы многочлены Доказательство. Если Корни квадратного уравнения
Пусть дано квадрат
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.92.5 (0.014 с.) |

 – элемент множества
– элемент множества  , то пишут
, то пишут  , в противном случае ─
, в противном случае ─  . Если
. Если  - некоторые элементы множества
- некоторые элементы множества  означает, что множество
означает, что множество  . Если
. Если  . Если в
. Если в  , или
, или  (
(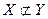 .
. означает, что «существует элемент
означает, что «существует элемент  означает: «для любого
означает: «для любого  найдется
найдется  , зависящее от
, зависящее от  и большее 0…».
и большее 0…».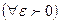


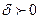 такое, что для всех
такое, что для всех  и удовлетворяющих неравенству
и удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
. ;
;  ). Иррациональное число представляется непериодической бесконечной десятичной дробью (
). Иррациональное число представляется непериодической бесконечной десятичной дробью ( ; p = 3,14159…).
; p = 3,14159…). , число (-
, число (-  .
. . Таким образом,
. Таким образом,  , если
, если  , если
, если  . Доказательство. Если
. Доказательство. Если  , то
, то  . Если
. Если  , то
, то  , но
, но  , т. е.
, т. е.  .
. . Доказательство. Если
. Доказательство. Если  и тогда
и тогда  . Если
. Если  .
. . Доказательство. Если
. Доказательство. Если  ,
,  , т. е.
, т. е.  . Если
. Если  . Так как
. Так как  , или
, или  , откуда
, откуда  , т. е.
, т. е.  . Поэтому
. Поэтому  |. Получаем, что
|. Получаем, что  положительное число. Тогда неравенства
положительное число. Тогда неравенства  и
и  равносильны. ((" e, e > 0: |х| £ e) Û (- e £ х £ e)).
равносильны. ((" e, e > 0: |х| £ e) Û (- e £ х £ e)). , таким образом,
, таким образом,  . Если
. Если  , откуда
, откуда  . Объединяя неравенства
. Объединяя неравенства  ,
, 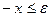 . По определению,
. По определению,  , поэтому
, поэтому  .
. – произвольные числа. По свойству 3 для них выполняются неравенства:
– произвольные числа. По свойству 3 для них выполняются неравенства:  ,
,  . Поэтому, складывая эти неравенства, получаем
. Поэтому, складывая эти неравенства, получаем  . По предыдущей теореме это равносильно неравенству
. По предыдущей теореме это равносильно неравенству  .
. .
. . По предыдущей теореме
. По предыдущей теореме  . Поэтому
. Поэтому  .
. и
и  , если
, если  . Эти соотношения предлагается доказать самостоятельно.
. Эти соотношения предлагается доказать самостоятельно. Выберем на плоскости некоторую точку О (полюс) и некоторый выходящий из нее луч Ох и укажем единицу масштаба.
Выберем на плоскости некоторую точку О (полюс) и некоторый выходящий из нее луч Ох и укажем единицу масштаба.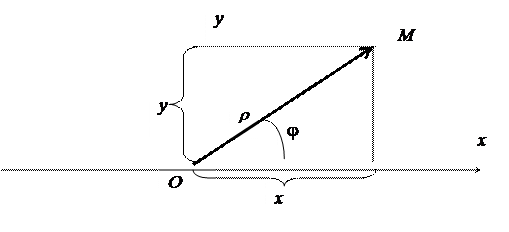
 . (1.1)
. (1.1) . (1.2)
. (1.2) (если у > 0) и
(если у > 0) и  (если у < 0).
(если у < 0).




 справедливо равенство
справедливо равенство  .
. :
:  , т. е. 1=1 - верно; б) пусть это утверждение справедливо для некоторого натурального
, т. е. 1=1 - верно; б) пусть это утверждение справедливо для некоторого натурального  , т. е.
, т. е.  . Тогда при
. Тогда при  имеем:
имеем: 
 =
= 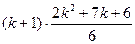 =
=  =
=  , т. е. утверждение верно и для
, т. е. утверждение верно и для  .
.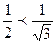 - верно; б) пусть это утверждение справедливо для некоторого натурального
- верно; б) пусть это утверждение справедливо для некоторого натурального  . Тогда при
. Тогда при 
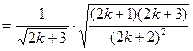 =
= 
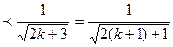 , т. е. утверждение верно и для
, т. е. утверждение верно и для  , где
, где  ,
,  вычисляется по формуле
вычисляется по формуле . (1.7)
. (1.7) , т. е.
, т. е. 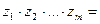
 . Тогда при
. Тогда при  имеем:
имеем:

 , т. е. утверждение верно и для
, т. е. утверждение верно и для  с учетом формулы (1.7) получим:
с учетом формулы (1.7) получим: . (1.8)
. (1.8) , то получается знаменитая формула Муавра:
, то получается знаменитая формула Муавра: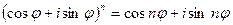 . (1.9)
. (1.9) ,
,  .
. =
=  . Положим теперь
. Положим теперь 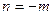 , считая m целым положительным. Тогда
, считая m целым положительным. Тогда  =
=  =
=  =
=  =
= 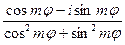 =
= 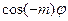 +
+  =
=  . Таким образом, формула Муавра оказывается верной при всех целых значениях n.
. Таким образом, формула Муавра оказывается верной при всех целых значениях n.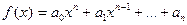 и
и  . Найдутся многочлен
. Найдутся многочлен  и число
и число  такие, что
такие, что  .
. . Из равенства
. Из равенства  =
=  при сравнении коэффициентов получаем цепочку равенств:
при сравнении коэффициентов получаем цепочку равенств:  ,
,  ,
,  ,...,
,..., 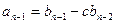 ,
,  , откуда последовательно определяются коэффициенты
, откуда последовательно определяются коэффициенты  ,
,  ,
, ,…,
,…,  ,
, .
. на линейный двучлен
на линейный двучлен  .
.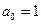









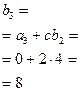


 , остаток 32.
, остаток 32.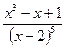 .
. по степеням
по степеням 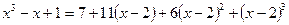 . Следовательно,
. Следовательно,  .
. , где многочлен
, где многочлен  уже не делится на
уже не делится на  , то число к называется кратностью корня с в многочлене
, то число к называется кратностью корня с в многочлене 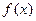 , а сам корень с – к -кратным корнем этого многочлена. Если к = 1, то говорят, что корень с простой.
, а сам корень с – к -кратным корнем этого многочлена. Если к = 1, то говорят, что корень с простой. оно будет (к −1)-кратным корнем первой производной этого многочлена. Если же
оно будет (к −1)-кратным корнем первой производной этого многочлена. Если же 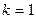 , то с не будет служить корнем для
, то с не будет служить корнем для  .
. ,
,  . В выражении для
. В выражении для 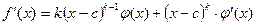 . Первое слагаемое в этой сумме делитсяна
. Первое слагаемое в этой сумме делитсяна  , а второе – на
, а второе – на 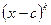 , следовательно, с − (к −1)-кратный корень для
, следовательно, с − (к −1)-кратный корень для  , но не является корнем для
, но не является корнем для  , то в этом случае с − к -кратный корень многочлена
, то в этом случае с − к -кратный корень многочлена 
 ?
? имеем
имеем  . Найдем
. Найдем  ;
; 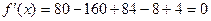 . Найдем
. Найдем  :
:  ;
;  . Производная 3-го порядка:
. Производная 3-го порядка:  ;
;  , таким образом, кратность корня 2 для многочлена
, таким образом, кратность корня 2 для многочлена  называется многочлен
называется многочлен  наибольшей степени среди многочленов, делящих оба многочлена
наибольшей степени среди многочленов, делящих оба многочлена  . Другими словами, наибольшим общим делителем двух отличных от нуля многочленов
. Другими словами, наибольшим общим делителем двух отличных от нуля многочленов  ,
,  ;
;  ,
,  ;
;  ,
,  ; …;
; …;  ,
,  ,
,  .
. и будет наибольшим общим делителем для многочленов
и будет наибольшим общим делителем для многочленов  .
. и
и  в кольце вещественных чисел.
в кольце вещественных чисел. ,
, 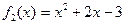 . Найдем остаток
. Найдем остаток  :
: . Найдем остаток
. Найдем остаток  . Для этого многочлен
. Для этого многочлен  разделим на
разделим на  , следовательно, для многочленов
, следовательно, для многочленов  и
и  наибольшим общим делителем является
наибольшим общим делителем является  , где
, где  и
и  − некоторые многочлены. Можно считать при этом, что если степени многочленов
− некоторые многочлены. Можно считать при этом, что если степени многочленов  ,
,  ,
,  , …,
, …,  ,
,  . Получили, что
. Получили, что  . Возвращаясь назад, придем к доказываемому равенству.
. Возвращаясь назад, придем к доказываемому равенству. и
и  найти такие многочлены
найти такие многочлены  и
и 
 .
. . Используя обратный ход в алгоритме Евклида, получим
. Используя обратный ход в алгоритме Евклида, получим 
 . После раскрытия скобок получим
. После раскрытия скобок получим  ,
,  .
. и
и  .
.


 ,
,  ,
,  . Далее
. Далее  .
.




 . С другой стороны,
. С другой стороны,  . Далее
. Далее  .
.


 , т. е.
, т. е.  . Учитывая, что
. Учитывая, что 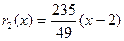 , получим
, получим 
 , т. е.
, т. е.  ,
,  .
. и
и  и
и  такие, что
такие, что 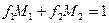 .
. .
.


