
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Над многочленами. Корни многочленов. Теорема БезуСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Одночленом от переменной Считается, что Определение. Одночлены называются подобными, если показатели степени Подобные одночлены складываются по правилу Определение. Многочленом n -й степени от неизвестного х называется сумма целых неотрицательных степеней, не превышающих п, неизвестного х, взятых с некоторыми числовыми коэффициентами, т. е. выражение вида
причем В многочлене порядок слагаемых безразличен, и подобные одночлены можно соединять по правилу приведения подобных членов. Запись (2.1) называется канонической формой многочлена. Иногда удобно записывать многочлены в порядке возрастания показателей. Многочлены обозначаются Пусть Определение. Два многочлена называются равными (или тождественно равными), если они составлены в канонической записи из одинаковых одночленов, т.е. Иными словами, в равных многочленах равны коэффициенты при одинаковых степенях неизвестного х. Определение. Суммой двух многочленов называется многочлен, получающийся при объединении одночленов, составляющих слагаемые. После объединения необходимо привести подобные члены. Таким образом, Определение. Произведением двух многочленов называется многочлен, составленный из произведений всех членов первого сомножителя на все члены второго. После приведения подобных членов получим, что Коэффициент при Пусть даны два многочлена Для любых двух многочленов
причем степень Определение. Пусть даны два ненулевых многочлена Определение. Если Теорема. Остаток от деления многочлена Доказательство. Согласно (2) П р и м е р. Найти остаток от деления многочлена Решение. По доказанной ранее теореме Если для полиномов Теорема (Безу). Для того чтобы полином Доказательство. А. Необходимость. Пусть Определение. Число с называется корнем полинома С использованием этого определения теорема Безу может быть сформулирована следующим образом: для того чтобы полином П р и м е р. Является ли линейный многочлен Решение. Найдем
Схема Горнера
Теорема. Пусть Доказательство. Будем искать
Теорема доказана. Более того, получен очень удобный способ вычисления коэффициентов П р и м е р. Найти неполное частное и остаток от деления многочлена Решение. Составим таблицу:
Таким образом, неполное частное П р и м е р. Пользуясь схемой Горнера, разложить на простейшие дроби выражение Решение. Разложим числитель
Таким образом,
Кратные корни
Определение. Если Теорема. Если число с является к -кратным корнем многочлена Доказательство. Пусть Следствие. Если число с является корнем для П р и м е р. Чему равен показатель кратности корня 2 для многочлена Решение. При
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.242.20 (0.01 с.) |

 с коэффициентом из множества А называется выражение вида
с коэффициентом из множества А называется выражение вида  , где
, где 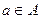 ,
, 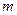 − целое неотрицательное число.
− целое неотрицательное число. , поэтому все элементы множества А являются одночленами частного вида.
, поэтому все элементы множества А являются одночленами частного вида.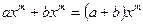 , которое называется правилом приведения подобных членов. Для одночленов определяется и действие умножения
, которое называется правилом приведения подобных членов. Для одночленов определяется и действие умножения  .
. , (2.1)
, (2.1)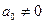 .
.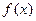 ,
,  ,
,  и т. д.
и т. д.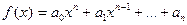 , причем
, причем 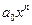 называется высшим (старшим) членом многочлена
называется высшим (старшим) членом многочлена 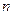 − степенью многочлена
− степенью многочлена  . Нулевой многочлен не имеет высшего члена в смысле данного определения и считается, что он равен 0. Степень нулевого многочлена считается равной символу
. Нулевой многочлен не имеет высшего члена в смысле данного определения и считается, что он равен 0. Степень нулевого многочлена считается равной символу 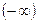 .
.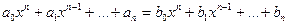 в том и только в том случае, если
в том и только в том случае, если 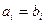 ,
, 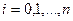 .
.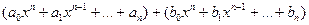 =
= 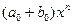 +
+ 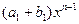 + … + +
+ … + + 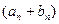 .
.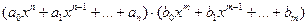 =
= 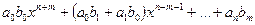 .
.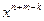 равен
равен  , если считать, что
, если считать, что 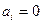 при
при 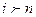 и
и 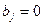 при
при 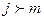 .
. , причем
, причем 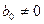 . Тогда произведение
. Тогда произведение  содержит ненулевой одночлен, который будет высшим для произведения данных многочленов, так как остальные произведения членов
содержит ненулевой одночлен, который будет высшим для произведения данных многочленов, так как остальные произведения членов 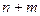 степень.
степень. и
и  , что
, что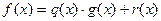 , (2.2)
, (2.2)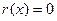 . Многочлены
. Многочлены  , то
, то 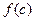 называется значением многочлена
называется значением многочлена 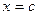 .
. равен значению
равен значению  , где
, где  − многочлен нулевой степени, т. е. константа. Переходя в этом равенстве к значениям при
− многочлен нулевой степени, т. е. константа. Переходя в этом равенстве к значениям при 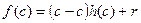 , откуда
, откуда 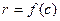 . Теорема доказана.
. Теорема доказана.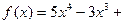
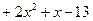 на многочлен
на многочлен  .
.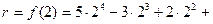
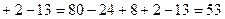 .
. , что
, что  , то говорят, что полином
, то говорят, что полином  .
.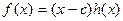 . Тогда
. Тогда 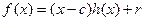 будет
будет  , т. е.
, т. е.  делителем многочлена
делителем многочлена 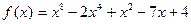 ?
?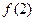 :
:  , следовательно,
, следовательно,  .
. . Из равенства
. Из равенства  =
=  при сравнении коэффициентов получаем цепочку равенств:
при сравнении коэффициентов получаем цепочку равенств:  ,
,  ,
,  ,...,
,..., 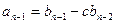 ,
,  , откуда последовательно определяются коэффициенты
, откуда последовательно определяются коэффициенты  ,
,  ,
, ,…,
,…,  ,
, .
. на линейный двучлен
на линейный двучлен 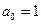









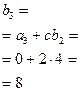


 , остаток 32.
, остаток 32.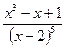 .
. по степеням
по степеням 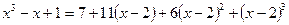 . Следовательно,
. Следовательно,  .
. , где многочлен
, где многочлен  оно будет (к −1)-кратным корнем первой производной этого многочлена. Если же
оно будет (к −1)-кратным корнем первой производной этого многочлена. Если же 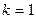 , то с не будет служить корнем для
, то с не будет служить корнем для  .
. ,
,  . В выражении для
. В выражении для 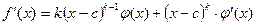 . Первое слагаемое в этой сумме делитсяна
. Первое слагаемое в этой сумме делитсяна  , а второе – на
, а второе – на 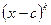 , следовательно, с − (к −1)-кратный корень для
, следовательно, с − (к −1)-кратный корень для  , но не является корнем для
, но не является корнем для  , то в этом случае с − к -кратный корень многочлена
, то в этом случае с − к -кратный корень многочлена 
 ?
? имеем
имеем  . Найдем
. Найдем  ;
; 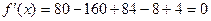 . Найдем
. Найдем  :
:  ;
;  . Производная 3-го порядка:
. Производная 3-го порядка:  ;
;  , таким образом, кратность корня 2 для многочлена
, таким образом, кратность корня 2 для многочлена 


