
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление множеств в ЭВМСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Множества и их элементы Для множества не существует строгого определения, поэтому введем описательные понятия множества и его элементов. Множеством называется совокупность некоторых предметов, объединенных общим признаком. Элементы множества – это те предметы, из которых состоит множество. Пусть имеется множество А, элементом которого является предмет а. Это записывается как А={а}. Например, А={1, 2, 3}. Если какой-то элемент а принадлежит множеству А, то это обозначается аÎА, а если b не принадлежит А, то bÏА. Например, пусть А – множество четных натуральных чисел, тогда 6ÎА, а 3ÏА. Пусть имеется два множества А и В, причем все элементы множества А принадлежат множеству В, т.е. если хÎА, то хÎB. В этом случае говорят, что множество А включено в множество В. Обозначается: АÍВ (Í – символ нестрогого включения, т.е. возможно совпадение множеств). Множество А совпадает с множеством В (А = В), если все элементы множества В являются элементами множества В и все элементы множества В являются элементами множества А. Это можно записать в виде (А Í В и В Í А) Û (А = В). Множество А строго включено в множество В, если все элементы множества А принадлежат множеству В, но не все элементы множества В принадлежат множеству А. Например: А = { 1, 2, 3 }, В = { 0, 1, 2, 3 }, АÌВ. Способы задания множеств. Возможны два способа задания множества. 1. Перечислением элементов, т.е. в фигурных скобках дается полное перечисление элементов данного множества. Например: N = {1,2,...,n,...} – множество натуральных чисел. 2. С помощью указания характерного свойства (указание свойства, которым обладают только элементы данного множества). Символически это записывается в виде A={x | P(x)} и читается: A есть множество всех элементов х, обладающих свойством P(x). При задании множества вторым способом возможны различные противоречия и парадоксы. Рассмотрим примеры таких парадоксов. 1) Парадокс парикмахера: в городе жил парикмахер, который брил всех, кто не брился сам. Кто же брил парикмахера? 2) Пусть имеем натуральное число 11218321 – одиннадцать миллионов двести восемнадцать тысяч триста двадцать один. Это число можно описать с помощью восьми слов. Пусть А – множество натуральных чисел, которые нельзя определить с помощью фразы, имеющей меньше 20 русских слов. Обозначим аmin – наименьшее число из множества А, причем аminÎA. Число аmin можно определить следующим образом: наименьшее натуральное число, которое нельзя определить с помощью фразы, имеющей менее двадцати слов. В этой фразе 14 слов. Значит, аmin можно определить с помощью фразы, содержащей менее 20 слов. Тогда получается, что аminÏ А. Существует много подобных примеров, когда определение множества оказывалось внутренне противоречиво, однако, выяснение условий, при которых это может иметь место, требует специальных исследований, составляющих предмет математической логики, и выходит за рамки собственно теории множеств. Поэтому в дальнейшем изложении мы не станем касаться спорных случаев, и будем рассматривать лишь множества, которые определяются точно и без противоречий. В теории множеств имеется специальное множество, называемое пустым множеством (Æ), которое не содержит ни одного элемента. Пустое множество по определению содержится в любом множестве А (ÆÍА, " A). Это понятие вводится из следующих соображений. Задавая множество вторым способом не всегда заранее можно быть уверенным, существуют ли элементы, ему принадлежащие. Например, можно говорить о множестве четырехугольников на плоскости, у которых все углы прямые, а диагонали не равны. Только знания основ геометрии позволяют убедиться, что таких четырехугольников не существует и, следовательно, это множество пусто. Доказательства в теории множеств. Большинство утверждений теории множеств связано с равенством двух множеств или включением одного множества в другое. Поэтому надо детально разобраться в методах доказательства этих фактов. 1. Доказательство включения АÍВ. Для этого нужно доказать, что любой элемент x, принадлежащий множеству А одновременно является элементом множества В, т.е. (" x Î А) Þ (x Î В). 2. Доказательство равенства А = В. Оно сводится к доказательству двух включений А Í В и В Í А. Пример 1. Докажем следующую теорему. Для любых множеств А, В и С выполняется закон транзитивности нестрогого включения, т.е. если а) А Í В и б) В Í С, то из этого следует, что АÍС. Доказательство. Пусть x – любой элемент множества А, (xÎА), тогда в силу условия А Í В, по определению нестрогого включения, элемент х принадлежит также и множеству В (хÎB). Аналогично, используя условие В Í С, можно доказать, что х принадлежит С (хÎС). Итак, в качестве исходного допущения мы приняли, что x – любой элемент из А. Из этого допущения при выполнении условий а) и б) получено следствие хÎС. По определению нестрогого включения это означает А Í С, что и требовалось доказать.
Операции над множествами Определим следующие операции. 1. Объединение. Пусть А и В – произвольные множества. Их объединением называется множество С = А È В, которое состоит из всех элементов, принадлежащих хотя бы одному из множеств А или В. 2. Пересечение. Пересечением множеств А и В называется множество С, состоящее из элементов, одновременно принадлежащих А и В. Обозначается так: C = A Ç B. 3. Разность. Разность множеств А и В – это множество С (С = А \ В), состоящее из элементов множества А, не принадлежащих множеству В. Если В Í А, то разность С = А \ В называется дополнением В до А. Считается, что все множества включены в некоторое множество U, которое называют универсальным множеством (универсумом). В этом случае дополнение какого-либо множества А до U обозначается С (А) или 4. Симметричная разность. По определению симметричная разность двух множеств А и В – это множество С = А D В = (А \ В) È (В \ А). Перечисленные операции удобно изображать графически с помощью т.н. диаграмм Вена (показать). Основные свойства операций 1. Коммутативность: А Ç В = В Ç А; А È В = В È А. 2. Ассоциативность: (А Ç В) Ç С = А Ç (В Ç С) = А Ç В Ç С; (А È B) È С = А È (В È С) = А È В È С. Свойствами коммутативности и ассоциативности обладают многие операции. Чтобы не создалось впечатления, что коммутативность и ассоциативность являются общими свойствами всех операций приведем пример неассоциативной операции – возведение в степень: (23)2 = 82 = 64; 3. Взаимная дистрибутивность: а) (А È В) Ç С = (А Ç С) È (В Ç С); б) (А Ç B) È С = (А È С) Ç (В È С). Для вещественных чисел выполняется свойство дистрибутивности операции умножения относительно сложения a(b + с) = аb + ас. Операции È и Ç множеств – взаимно дистрибутивны: Докажем равенство а). Предположим, что xÎ(А È В) Ç С, тогда xÎС и xÎА или xÎВ. Рассмотрим первый случай xÎС и xÎА. Тогда хÎА Ç С, а значит, по определению объединения, хÎ(А Ç С) È (В Ç С). (Можно объединить с любым множеством) Во втором случае, т.е. при xÎС и xÎВ получаем, что xÎ (В Ç С) È (А Ç С). Таким образом, мы доказали включение [(А È В) Ç С] Í [(А Ç С) È (В Ç С)]. Докажем обратное включение. Пусть хÎ(А Ç С) È (В Ç С), тогда либо хÎА Ç С либо хÎВ Ç С. В первом случае хÎА и хÎС. Во втором случае хÎВ и xÎС. В обоих случаях получаем, что хÎС и хÎА или хÎВ.Следовательно, хÎ (А È В) Ç С. Тем самым доказано включение (А Ç С) È (В Ç С) Í (А È В) Ç С. Из этих включений следует, что (А È В) Ç С = (А Ç С) È (ВÇС), что и требовалось доказать. 4. Идемпотентность: A È A = A; A Ç A = A. 5. Законы поглощения: (A Ç B) È A = A; (A È B) Ç A = A. 6. Свойства нуля: A È Æ =A; A Ç Æ = Æ. 7. Свойства единицы: A È U =U; A Ç U = A. 8. Инволютивность: 9. Законы де Моргана: 10. Свойства дополнения: Законы де Моргана можно обобщить на произвольное количество множеств. Пусть А1, А2,... – некоторые множества и пусть все они включены в S (А1, А2,... Í S). Тогда выполняются следующие соотношения. 11. 12. Докажем свойство 11. Пусть хÎ Обратно, пусть хÎ Отображения Пусть Х – некоторое числовое множество. Говорят, что на множестве Х определена функция f, если каждому числу xÎХ ставится в соответствие определенное число y = f(x). Множество Х – область определения функции, а множество Y = {f(x) | xÎX} – область значений функции. Если в качестве множеств Х и Y рассматривать множества произвольной природы, а не только числовые, мы приходим к понятию отображения. Def. Пусть X и Y – два произвольных множества. Говорят, что на X определено отображение f, принимающее значения из Y (f: X® Y), если каждому элементу x из X ставится в соответствие единственный элемент y = f(x) из Y. Множество элементов xÎX, для которых определено отображение f, называется областью определения f и обозначается df. Если имеется какой-либо элемент хÎX, то соответствующий ему элемент yÎY будем называть образом x. Пусть A – некоторое подмножество множества X (AÍX), образ множества A определяется как множество образов элементов множества A и обозначается f(A), т.е. f(A) = {f(x) | xÎA}. Образ области определения называется областью значений отображения f и обозначается rf (т.е. rf = f(df) = f(X)). Если задать yÎY, то множество соответствующих ему x, т.е. таких, что y = f(x), будем называть прообразом y и обозначать f –1(y), f –1(y) = {xÎX | y = f(x)}. В общем случае обратное отображение f –1 неоднозначно. Пусть B – некоторое подмножество множества Y (BÍY), прообраз множества B определяется как множество прообразов элементов множества B и обозначается f –1(B), т.е. f –1(B) = { xÎA | f(x) = y, y Î B}. Отображение i: X ® X такое, что i(x) = x для любого xÎX называется тождественным отображением. Пусть f: X ® Y и g: Y ® Z. Отображение h: X ® Z, такое, что каждому элементу xÎX ставится в соответствие единственный элемент h(x) = g(f(x)), называется композицией (или суперпозицией) отображений f и g и обозначается g о f. Отображение f: X ® Y называется сюръекцией X на Y, если множество образов всех элементов из X совпадают с множеством Y. Это обозначается как f(X) = Y. Другое эквивалентное определение сюръекции – это отображение, при котором каждый элемент из Y имеет прообраз в множестве X. Если для любых x1, x2ÎX таких, что x1 ¹ x2, получается, что f(x1) ¹ f(x2), т.е. разным элементам соответствуют различные образы, то это отображение f называется инъекцией. Отображение f, которое является одновременно сюръекцией и инъекцией, называется биекцией, или взаимно однозначным отображением. Если между А и В установлено биективное отображение, то говорят, что множества А и В эквивалентны. Эквивалентность множеств обозначается A ~ B. Легко видеть, что эквивалентность множеств обладает свойством транзитивности, т.е. если A ~ B и B ~ C, то A ~ C. Признаки эквивалентности множеств дают следующие Теоремы Кантора-Бернштейна 1. Если A Í B Í C, причем A ~ C, то A ~ B. 2. Если A эквивалентно подмножеству множества B, а B эквивалентно подмножеству множества A, то A ~ B. (Без доказательства). Основные свойства отображений можно сформулировать в виде следующих теорем. Теорема 1.1. f –1 (A È B) = f –1 (A) È f –1 (B) – прообраз объединения двух множеств равен объединению их прообразов. Доказательство. Пусть xÎf –1 (A) È f –1 (B). Тогда или xÎf –1 (A) или хÎf –1 (B). В первом случае y = f(x)ÎА, во втором yÎВ. В любом случае yÎА È В, поэтому xÎf –1 (A È B). Докажем обратное включение. Пусть xÎf –1 (A È B), тогда y = f(x) Î A È B. Значит или yÎА, или yÎВ. Если yÎА, то f –1 (y) Í f –1 (A). Так как xÎf –1 (y), то отсюда следует, что xÎf –1 (A). Если же yÎВ, то f –1 (y) Í f –1 (B), что влечет xÎf –1 (В). В любом случае xÎf –1 (A) È f –1 (B). Поэтому, если xÎf –1 (A È B), то xÎf –1 (A) È f –1 (B), что и требовалось доказать. Теорема 1.2. f –1 (A Ç B) = f –1 (A) Ç f –1 (B) – прообраз пересечения двух множеств равен пересечению их прообразов. Доказательство. Пусть xÎf –1 (A Ç B), тогда y = f(x)ÎA Ç B. Значит, yÎА и yÎВ. Если yÎА, то f –1 (y) Í f –1 (A), а если yÎВ, то f –1 (y) Í f –1 (B). Эти включения должны выполняться одновременно, следовательно, f –1 (y) Í f –1 (A) Ç f –1 (B), а значит, хÎf –1 (A) Ç f –1 (B). Таким образом, f –1 (A Ç B) Í f –1 (A) Ç f –1 (B). Докажем обратное включение. Пусть xÎf –1(A) Ç f –1(B), тогда xÎ f –1(A) и xÎf –1(B). Если xÎf –1(A), то y = f(x)ÎA. Если же xÎf –1(B), то y = f(x)ÎB. Так как yÎA и yÎB, то yÎAÇB и поэтому f –1(y) Í f –1(A Ç B). Значит, хÎf –1(A Ç B) и отсюда следует, что f –1(A) Ç f –1(B) Í f –1(A Ç B). Эти два включения означают, что f –1(AÇB) = f –1(A)Çf -1(B), что и требовалось доказать. Теорема 1.3. f (A È B) = f (A) È f (B) – образ объединения двух множеств равен объединению их образов. Доказательство. Пусть yÎf(A È B), тогда для любого x из множества f –1(y) выполняется принадлежность хÎA È B. Поэтому xÎA или xÎB. В первом случае y = f(x)Îf(A), во втором – y = f(x)Îf(B). Так как yÎf(A) или yÎf(B), то yÎf(A) È f(B) и, следовательно, f(A È B) Í f(A) È f(B). Докажем обратное включение. Пусть yÎf(A) È f(B), тогда yÎf(A) и f –1(y) Í A или yÎf(B) и f –1(y) Í B. Соответственно получаем, что xÎA или xÎB, т.е. xÎA È B и тогда y = f(x)Îf(A È B). Доказано включение f(A) È f(B) Í f(A È B). Следовательно, f(A È B) = f(A) È f(B). что и требовалось доказать. Замечание. Образ пересечения двух множеств не обязательно совпадает с пересечением их образов. Рассмотрим пример. Пусть A и B – множества точек на плоскости: A = { (x, y) | 0 £ x £ 1, y = 2 }, B = { (x, y) | 0 £ x £ 1, y = 1 }. С помощью проектирования точек на ось ОХ построим отображение А и В на множество С = { (x, y) | 0 £ x £ 1, y = 0 }. Так как f(A) = C, f(B) = C, то f(A) Ç f(B) = C. Но множества A и B не пересекаются и f(A Ç B) = f(Æ) = Æ, т.е. мы показали, что f(A Ç B) ¹ f(A) Ç f(B). Теоремы 1, 2, 3 остаются в силе при любом конечном и бесконечном числе множеств. Например, теорема 1.1 примет вид:
где A1, A2,... – некоторая система множеств. Докажем (1) с помощью метода математической индукции. 1. При n = 2 равенство f –1(A1 È A2) = f –1(A1) È f –1(A2) справедливо согласно теореме 1.1. 2. Предположим, что равенство верно при любом n £ k. 3. Докажем, что равенство верно при n = k+1. Обозначим B = Тогда f –1 так как для двух множеств В и Ak+1 теорема верна. Но по предположению индукции для k множеств теорема также верна, поэтому f –1 (B)= Отсюда следует требуемое равенство.
Тема 2. Мощность множества Понятие мощности Рассмотрим множество всех молекул в земной атмосфере. Это множество содержит очень большое число элементов (примерно 1.03∙1011), но оно конечное, т.е. существует такая константа, которая больше числа элементов этого множества. Помимо конечных существуют бесконечные множества. Одной из задач теории множеств является определение числа элементов множества и исследование вопроса о сравнении друг с другом двух множеств по количеству элементов. Для конечных множеств самой разной природы эта задача легко решается непосредственным подсчетом. Для бесконечных множеств вопрос о сравнении невозможно решить, как для конечных, с помощью подсчета. Поэтому Кантор предложил для сравнения двух бесконечных множеств установить между ними взаимно однозначное (биективное) отображение. Напоминаем, что множества, между которыми можно установить биективное отображение называются эквивалентными. Рассмотрим примеры установления такого отображения. Пример 2. В качестве множества А рассмотрим интервал на числовой прямой, пусть А = (–1, 1), а в качестве множества В – множество действительных чисел R. Эти множества эквивалентны, т.к отображение f(x) = tg(px/2), хÎА позволяет установить между ними искомое взаимно-однозначное соответствие. Пример 3. Пусть А = [–1, 1], В = (–1, 1). Строим отображение f: A ® B по следующему правилу: выделим в А последовательность –1, 1, 1/2, 1/3, 1/4,..., 1/n и положим f(–1) = 1/2, f(1) = 1/3, f(1/2) = 1/4, f(1/3)=1/5, т.е. f(1/n) = 1/(n+2), а все точки, не входящие в эту последовательность отобразим сами в себя, т.е. f(x) = х. Следовательно, открытый и замкнутый интервалы эквивалентны. Мощность множества является обобщением понятия числа элементов множества. Если взаимно однозначное отображение множеств установлено, значит, по определению, в обоих множествах “одинаковое” число элементов или мощность одного множества равна мощности другого множества. Мощность – это то общее, что есть у любых двух эквивалентных множеств. Мощность множества A обозначается m(A) или |A|. Таким образом, m(A) = m(B), если A ~ B. Если множество A эквивалентно какому-либо подмножеству множества B, то мощность A не больше мощности B (т.е. m(A) £ m(B)). Если при этом множество B не эквивалентно никакому подмножеству множества A, то m(A) < m(B). Особое место среди бесконечных множеств является множество натуральных чисел N. Def. Назовем счетным всякое множество, эквивалентное множеству N. Другими словами, счетным называется всякое множество, элементы которого можно перенумеровать или составить из них бесконечную последовательность. Примеры счетных множеств. 1. Множество целых чисел Z ={0, ±1, ±2,...}. Построим из его элементов последовательность: a1 = 0; a2= – 1; a3 = 1; a4 = –2; a5 = 2;... Формулу для вычисления ее общего члена можно записать в виде
2. Множество Q всех рациональных чисел. Докажем счетность этого множества. Как известно, рациональные числа – это дроби вида p/q, где pÎ Z, qÎ N. Запишем их в виде таблицы из бесконечного числа строк и столбцов
0/1 1/1 2/1 3/1... –1/1 –2/1 –3/1 –4/1... 1/2 2/2 3/2 4/2... –1/2 –2/2 –3/2 –4/2... ............. Обозначим это множество – А. Из ее элементов построим последовательность по следующему правилу a1=0/1; a2=1/1; a3= –1/1; a4=1/2; a5= –2/1; a6=2/1 и т.д. Очевидно, в эту последовательность войдут все рациональные числа. Более того, в ней многие числа будут повторяться. Следовательно, m(Q) ≤ m(A). С другой стороны, эта последовательность эквивалентна натуральному ряду, т.е. подмножеству множества Q, а значит, m(A) = m(N) ≤ m(Q). Следовательно, m(Q) £ m(N) и m(N) ≤ m(Q), а, значит, мощности множеств рациональных чисел и натурального ряда равны, т.е. множество рациональных чисел счетно. Бесконечное множество не являющееся счетным называется несчетным.
Свойства счетных множеств 1. Всякое подмножество счетного множества конечно или счетно. Доказательство. Пусть А – счетное множество и B Í А. Поскольку А счетно, то занумеруем его элементы и построим из них последовательность a1, a2, a3,... Из этой последовательности выделим все элементы, принадлежащие множеству B, т.е. рассмотрим подпоследовательность
Возможны следующие случаи: 1) Множество B конечно – тогда теорема верна. 2) Множество B бесконечно. Поскольку элементы множества B занумерованы, то в этом случае оно является счетным, что и требовалось доказать. 2. Объединение любого конечного или счетного множества счетных множеств снова является счетным. Доказательство. Пусть множества А1, A2,..., Аn,... – счетные. Если их число не более, чем счетно, то множества можно занумеровать и расположить принадлежащие им элементы в таблицу А1 = {a11, a12, a13,...} А2 = {a21, a22, a23,...} А3 = {a31, a32, a33,...} ................. Пусть B = b1 = a11, b2 = a12, b3 = a21, b4 = a31, b5 = a22,... (1) Если множества Аi попарно пересекаются (Аi ÇАj ¹ Æ), то в последовательность (1) не включаются те элементы, которые уже занумерованы. Таким образом, построено взаимно однозначное соответствие между множествами B и N. Следовательно, множество B счетно. 3. Всякое бесконечное множество содержит счетное подмножество. Доказательство. Пусть М – произвольное бесконечное множество. Выберем в нем произвольный первый элемент и обозначим его a1, затем – элемент a2 и т.д. Получаем последовательность a1, a2,..., которая не может оборваться на каком-то элементе, т.к. М бесконечно. Следовательно, данная последовательность образует счетное подмножество множества М. Доказанная теорема позволяет утверждать, что среди бесконечных множеств счетное множество является самым "маленьким". Если множество конечно или счетно то говорят, что оно не более, чем счетно. Примеры несчетных множеств Рассмотренные примеры и свойства могут создать впечатление, что все бесконечные множества счетны. Однако, это далеко не так, и для доказательства этого достаточно построить контрпример, т.е. предъявить бесконечное множество, не являющееся счетным. Теорема 2.1. Множество всех бесконечных бинарных последовательностей, т.е. состоящих из 0 и 1, несчетно. Доказательство. Предположим противное, т.е. что эти последовательности можно занумеровать. Пусть P1, P2,... – последовательности, где P1 = {a11, a12, a13,...}, P2 = {a21, a22, a23,...} и т.д., где аij = 0 или аij = 1. Построим последовательность P, не содержащуюся в этом списке. Такая последовательность существует, например, P ={1– a11, 1–a22, 1–a33,...}. Очевидно, что ее элементы равны 0 или 1, причем она не равна никакой другой последовательности из списка, потому что отличается от P1 по крайней мере первым элементом, от P2 – по крайней мере вторым и т.д. Таким образом, построенная последовательность отличается от любой из занумерованных последовательностей хотя бы одним элементом. Следовательно, множество всех бинарных последовательностей занумеровать невозможно, а это означает, что оно несчетно. Другим важным примером бесконечного несчетного множества является множество вещественных (действительных) чисел R. Перечислим основные свойства действительных чисел. 1. Любое вещественное число можно представить конечной или бесконечной десятичной дробью. И обратно, для любой десятичной дроби существует вещественное число, которое она представляет. 2. Множество вещественных чисел является непрерывным, т.е. оно сплошь заполняет числовую ось. Задание. Доказать, что множество вещественных чисел несчетно. Указание: воспользоваться способом доказательства несчетности множества бинарных последовательностей.
Понятие нечеткого множества Во многих прикладных задачах, решаемых с помощью теории множеств, бывает сложно однозначно и четко ограничить набор элементов, принадлежащих данному множеству, т.к. возникает противоречие между формальной природой математики и привычкой человека мыслить неопределенными, расплывчатыми понятиями. (Куча камней это сколько штук? 5 слонов – это много, 10 муравьев – это мало и т.д.). Введением понятия нечеткого множества удалось в определенной мере преодолеть это противоречие. Пусть Е – универсальное множество, x – элемент E, а Р – некоторое свойство. Обычное (четкое) подмножество A универсального множества E, элементы которого удовлетворяют свойству Р, определяется как множество упорядоченных пар A = {mA(х) | x }, (1) где mA(х) – характеристическая функция, принимающая значение 1, если x удовлетворяет свойству Р, и 0 – в противном случае. Нечеткое подмножество отличается от обычного тем, что для элементов x из E нет однозначного ответа “да-нет” относительно свойства Р. В связи с этим, нечеткое подмножество A универсального множества E определяется как множество упорядоченных пар вида (1) где mA(х) – характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения уже в некотором вполне упорядоченном множестве M (например, M = [ 0, 1 ]). Функция принадлежности указывает степень (или уровень) принадлежности элемента x подмножеству A. Множество M называют множеством принадлежностей. Если M = { 0, 1 }, то нечеткое подмножество A может рассматриваться как обычное или четкое множество. Примеры записи нечеткого множества Пусть E= {x1, x2, x3, x4, x5 }, M = [ 0, 1 ]; A – нечеткое множество, для которого mA(x 1) = 0,3; mA(x 2)=0; mA(x 3)=1; mA(x 4)=0,5; mA(x 5)=0,9. Тогда A можнопредставить в виде: A = { 0,3 / x1; 0 / x2; 1 / x3; 0,5 / x4; 0,9 / x5 } или A = 0,3/x1 È 0/x2 È 1/x3 È 0,5/x4 È 0,9/x5, или
Примеры нечетких множеств 1. Пусть E = {0, 1, 2,.., 10}, M =[0, 1]. Нечеткое множество “несколько” можно определить следующим образом: “несколько”= 0,5/3 È 0,8/4 È 1/5 È 1/6 È 0,8/7 È 0,5/8; его характеристики:высота= 1, носитель = {3, 4, 5, 6, 7, 8}. 2. Пусть E = {1, 2, 3,..., 100} и соответствует понятию “возраст“, тогда нечеткое множество “молодой”, может быть определено с помощью функции принадлежности вида
Примеры бинарных отношений Пусть A = B = R, пара (x, y) является точкой вещественной плоскости. Тогда бинарное отношение RА = { (x, y) | x2 + y2 £ 1 } определяет замкнутый круг единичного радиуса с центром в точке (0, 0) на плоскости, отношение RБ = { (x, y) | x ³ y } полуплоскость, а отношение RВ= { (x, y) | |x – y| £ 2 } полосу. Диагональ множества A´A, т.е. множество D={(x,x) | xÎA}, называется единичным бинарным отношением или отношением равенства в A. Областью определения бинарного отношения R называется множество dR = { xÎA | $ yÎB, (x, y) ÎR }– множество первых элементов пар (x, y). Областью значений бинарного отношения R называется множество rR = { yÎB | $ xÎA, (x, y)ÎR }– множество вторых элементов пар (x, y). Как для любых множеств, для бинарных отношений можно определить понятия нестрогого и строгого включения и равенства. Так, например, R1 содержится в R2 (R1 Í R2), если любая пара (x, y), которая принадлежит отношению R1 а также принадлежит и отношению R2. Например, RА Í RВ, т.к. все точки (x, y), принадлежащие кругу RА принадлежат также полосе Rв. Операции над бинарными отношениями определяются подобно операциям над соответствующими множествами. Пусть А – произвольное множество на котором введены бинарные отношения R, R1, R2,... 1) Объединение двух бинарных отношений R1 и R2 – это отношение R1 È R2 = { (x, y) | (x, y)ÎR1 или (x, y)ÎR2 }. 2) Пересечение двух бинарных отношений R1 и R2 – это отношение R1 Ç R2 = { (x, y) | (x, y)ÎR1 и (x, y)ÎR2 }. 3) Обратное отношение R –1 = { (x, y) | (y, x)ÎR}. 4) Дополнение к отношению 5) Двойственное отношение Rd = 6) Композиция (суперпозиция) отношений R = R1oR2 содержит пару (x, y) тогда и только тогда, когда существует такое zÎA, что (x, z)ÎR1 и (z, y)ÎR2. Доказательства Свойство 2. Пусть пара (x, y)Î(È Rk) –1. Тогда (y, x)ÎÈ Rk. Это означает, что найдется отношение Rj, что (y, x)Î Rj. Отсюда, по определению обратного отношения, (x, y)ÎRj–1, а значит, (x, y)ÎÈRk–1и (ÈRk)–1 Í È Rk–1. Докажем обратное включение. Пусть (x,y)Î Rk–1 Это означает, что найдется такое множество Rj, что (x,y)ÎRj–1. Следовательно, (y, x)ÎRj и (y, x)Î ÈRk, поэтому (x, y)Î(È Rk)–1. Значит, È Rk–1 Í (ÈRk)–1. Одновременное выполнение обоих включений означает равенство множеств, что и требовалось доказать. Свойство 6. Пусть (x, y)Î(R1 Ç R2) o R3. По определению композиции это означает, что найдется такое zÎA, что (x, z)Î(R1 Ç R2) и (z, y)ÎR3. Первое включение возможно только тогда, когда одновременно выполнено (x, z)ÎR1 и (x, z)ÎR2. Это, в свою очередь, означает, с учетом (z, y)ÎR3, что одновременно (x, y)Î R1 o R3 и (x, y)ÎR2 o R3, а, следовательно, (x, y)Î(R1 o R3) Ç (R2 o R3), что и доказывает требуемое соотношение. Замечание. Покажем, почему неверно обратное включение. Пусть (x, y) Î(R1 o R3) Ç (R2 o R3), тогда (x, y) Î(R1 o R3) и (x, y) Î(R2 o R3). Первое включение означает существование такого элемента z1 из A, что (x, z1)ÎR1 и (z1, y) ÎR3; второе – существование такого z2ÎA, что (x, z2)ÎR2 и (z2, y)ÎR3, причем необязательно z1 = z2. Значит, не всегда существует такой элемент z, что (x, z)ÎR1 и (x, z)ÎR2, а, следовательно, не будет принадлежности пересечению R1 и R2. Свойство 7в. Возьмём любую пару (x, y)ÎR1, что эквивалентно (y, х)ÎR1–1. Пусть теперь R1 Í R2, т.е. из (x, y)ÎR1 следует (x, y)ÎR2. Перейдя к обратным отношениям, получим, что из (y, х)ÎR1–1 вытекает (y, х)ÎR2–1, что и означает требуемое свойство. Свойство 8а). Докажем предварительно равенство Пусть (x, y)Î Для доказательства свойства 8а) воспользуемся доказанным равенством и известными свойствами операций над множествами и отношениями.
(R1 È R2)d = = (`R1 Ç`R2)–1 =`R1–1 Ç R2–1 = R1d Ç R2d. 3. Способы задания отношений Традиционное задание отношений аналогично тому, как это принято в теории множеств, что не всегда удобно. Поэтому, наряду с таким заданием, применяются другие способы. 1. Матричное задание. Оно используется когда А – конечное или счетное множество А = {xi}. Тогда бинарное отношение R можно задавать с помощью матрицы R = {xij}, элементы которой определяются соотношением:
2. Табличное задание. Этим способом можно задавать произвольное n-арное отношение. Он используется, когда Аi – конечные или счетные множества Аi = {xij}. Строки таблицы соответствуют различным n-мерным элементам отношения, столбцы – наборам элементов из множеств Аi. 3. Задание с помощью графа. Для конечного или счетного множества А бинарное отношение можно задавать с помощью графа Г(R), который является геометрическим образом бинарного отношения. Граф – фигура состоящая из точек (вершин) соединенных линиями (дугами). Вершины графа соответствуют элементам множества А, то есть xi, а наличие дуги, соединяющей вершины xi и xj, означает, что (xi, xj)ÎR. Чтобы подчеркнуть упорядоченность пары на дуге ставится стрелка. Основные свойства графа. 1) Г(R–1) получается из Г(R) изменением направления стрелок на противоположные. 2) Граф Г(А´А) содержит дуги, соединяющие любую пару (xi, xj). Такой граф называется полным. 4. Задание верхними и нижними срезами. Этот способ может быть использован для любых множеств и бинарных отношений. Пусть на множестве А задано отношение R. Верхний срез GR(x) отношения R в точке x ÎА – это множество элементов yÎА таких, что (y, x)ÎR, т.е. GR(x) = { yÎA | (y, x)ÎR }. Если рассматривать R как отношение предпочтения, то GR (x) – это множество элементов, лучших, чем х. Нижний срез HR(x) отношения R в точке xÎА – это множество элементов yÎА, таких, что (x, y)ÎR, т.е. HR(x) = { yÎA | (x, y)ÎR }. Свойства нижних и верхних срезов |

 .
. = 28 = 512. Некоммутативной операцией является операция умножения матриц (АВ ¹ ВА).
= 28 = 512. Некоммутативной операцией является операция умножения матриц (АВ ¹ ВА). .
. ;
;  .
. ;
;  .
. – дополнение объединения множеств равно пересечению их дополнений.
– дополнение объединения множеств равно пересечению их дополнений. – дополнение пересечения множеств равно объединению их дополнений.
– дополнение пересечения множеств равно объединению их дополнений. , тогда хÏ
, тогда хÏ  , значит, x не принадлежит ни одному из множеств Ak ("k, хÏАk). Следовательно, по определению дополнения, хÎS\Аk для любого k. Отсюда вытекает, что хÎ
, значит, x не принадлежит ни одному из множеств Ak ("k, хÏАk). Следовательно, по определению дополнения, хÎS\Аk для любого k. Отсюда вытекает, что хÎ  .
. . Тогда этот элемент принадлежит каждому из множеств S \ Ak ("k, хÎS \ Ak). Следовательно, хÏAk для любого k, а, значит, хÏ
. Тогда этот элемент принадлежит каждому из множеств S \ Ak ("k, хÎS \ Ak). Следовательно, хÏAk для любого k, а, значит, хÏ 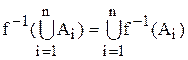 . (1)
. (1) .
. ) = f –1 (B È Ak+1) = f –1 (B) È f –1 (Ak+1),
) = f –1 (B È Ak+1) = f –1 (B) È f –1 (Ak+1),

 . Построим последовательность подобно тому, как это было сделано при доказательстве счетности Q.
. Построим последовательность подобно тому, как это было сделано при доказательстве счетности Q.
 ={ (x, y) | (x, y)Î(A´A) \ R}.
={ (x, y) | (x, y)Î(A´A) \ R}. .
. =
=  , то (x, y) ÏR–1 и (y, x)ÏR. Тогда (y, x)Î`R или, что то же самое, (x,y)Î(`R)–1.
, то (x, y) ÏR–1 и (y, x)ÏR. Тогда (y, x)Î`R или, что то же самое, (x,y)Î(`R)–1.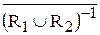 =
=  =
=



