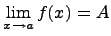Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расстояние от точки до плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предложение 11.1 Пусть плоскость
Доказательство. Расстояние от точки
Рис.11.9.Расстояние от точки до плоскости
Откуда
Координаты точки
Точка
32) В плоскости, в некоторой прямоугольной системе координат
где
может служить примером уравнения второй степени, определяющего мнимую кривую. Важные случаи общего уравнения кривой второго порядка. Перечислим шесть важнейших частных случаев общего уравнения (1): 1) Уравнение эллипса
с полуосями длины
с центром в начале координат и радиусом 2) Уравнение гиперболы
с полуосями 3) Уравнение параболы
4) Уравнение пары пересекающихся прямых
5) Уравнение пары параллельных или совпадающих прямых
6) Уравнение, определяющее точку,
Остановимся вкратце на перечисленных кривых Окружность. Окружностью называется геометрическое место точек, равноудаленных от одной и той же точки. Уравнение окружности имеет вид (x - a)2 + (y - b)2 = r 2, где a и b - координаты центра окружности, а r - радиус окружности. Если же центр окружности находится в начале координат, то ее уравнение имеет вид
x 2 + y 2 = r 2. Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами). Простейшее уравнение эллипса
где a - большая полуось эллипса, b - малая полуось эллипса. Если 2 c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение a 2 - b 2 = c 2. Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси
У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси.
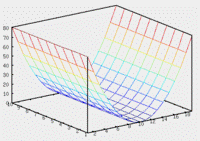
33) Поверхности второго порядка К невырожденным поверхностям второго порядка относятся эллипсоид, эллиптический параболоид, гиперболический параболоид, однополостной гиперболоид и двуполостной гиперболоид. Строгое изучение этих поверхностей проводится в курсе аналитической геометрии. Здесь же мы ограничимся определениями и иллюстрациями. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением Свойства эллиптического параболоида. 1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения. 2. Эллиптический параболоид обладает · осевой симметрией относительно оси Oz, · плоскостной симметрией относительно координатных осей Oxz и Oyz. 3. В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – парабола. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
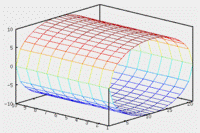
Свойства однополостного гиперболоида. 1. Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
2. Однополостной гиперболоид обладает · центральной симметрией относительно начала координат, · осевой симметрией относительно всех координатных осей, · плоскостной симметрией относительно всех координатных плоскостей. 3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола. Цилиндрические поверхности Поверхность Теорема (об уравнении цилиндрической поверхности). Кривая, задаваемая уравнением Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.
Конические поверхности
Коническая поверхность. Поверхность Функция Теорема (об уравнении конической поверхности). Если поверхность · Каноническое уравнение конуса второго порядка имеет вид:
34)
35) Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции. Другими словами, график функции y = f (х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x).
Способы задания функций
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций. Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции. Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента. Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции. Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания. Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами. Пример 1: функция E(x) — целая часть числа x. Вообще через E(x) = [ x ] обозначают наибольшее из целых чисел, которое не превышает x. Иными словами, если x = r + q, где r — целое число (может быть и отрицательным) и q принадлежит интервалу [0; 1), то [ x ] = r. Функция E(x) = [ x ] постоянна на промежутке [ r; r +1) и на нем [ x ] = r. Определения Рассмотрим систему несовпадающих точек
Задача интерполяции состоит в поиске такой функции
· Точки · Пары · Разность между «соседними» значениями · Функцию
36) 1) Квадратный корень, функция
[ 2) Показательная функция
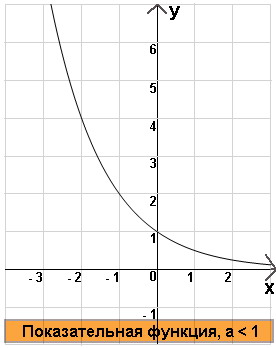
( 3) Показательная функция
( 4) Логарифмическая функция
5) Логарифмическая функция
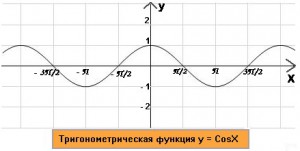
6) Тригонометрическая функция
7) Тригонометрическая функция
37)
38) 1. Предел переменной величины. Пусть переменная величина x в процессе своего изменения неограниченно приближается к числу 5, принимая при этом следующие значения: 4,9; 4,99;4,999;…или 5,1; 5,01; 5,001;… В этих случаях модуль разности стремится к нулю: = 0,1; 0,01; 0,001;… Число 5 в приведенном примере называют пределом переменной величины x и пишут lim x = 5. Определение 1. Постоянная величина a называется пределом переменной x, если модуль разности при изменении x становится и остается меньше любого как угодно малого положительного числа e. 1. Предел суммы Предел суммы равен сумме пределов, если каждый из них существует, т.е.
2. Предел разности Предел разности равен разности пределов, если каждый из них существует, т.е.
3. Предел постоянной величины Предел постоянной величины равен самой постоянной величине:
4. Предел произведения функции на постоянную величину Постоянный коэффициэнт можно выносить за знак предела:
5. Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.
6. Предел частного Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.
7. Предел степенной функции
где степень p - действительное число. 8. Предел показательной функции
где основание b > 0. 9. Предел логарифмической функции
где основание b > 0. 10. Теорема "о двух милиционерах" Предположим, что
то
То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу A.
39) Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю. Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака. Бесконечно малая величина Последовательность | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 задана уравнением
задана уравнением  и дана точка
и дана точка  . Тогда расстояние
. Тогда расстояние  от точки
от точки 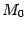 до плоскости
до плоскости 
 , опущенного из точки
, опущенного из точки 
 и нормальный вектор n плоскости
и нормальный вектор n плоскости  между ними равен 0 или
между ними равен 0 или  , если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому
, если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому

 , которые нам неизвестны, обозначим
, которые нам неизвестны, обозначим 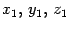 . Тогда
. Тогда 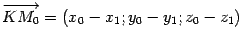 . Так как
. Так как  , то
, то  . Раскрыв скобки и перегруппировав слагаемые, получим
. Раскрыв скобки и перегруппировав слагаемые, получим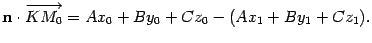
 . Отсюда находим, что
. Отсюда находим, что  . Подставив полученный результат в формулу (11.9), получим
. Подставив полученный результат в формулу (11.9), получим 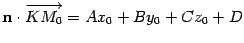 . Так как
. Так как  , то из формулы (11.8) следует формула (11.7).
, то из формулы (11.8) следует формула (11.7). ,
,  , пусть задана кривая, определяемая неявно уравнением второй степени
, пусть задана кривая, определяемая неявно уравнением второй степени , (1)
, (1) - заданные действительные числа. При этом числа
- заданные действительные числа. При этом числа 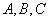 одновременно не равны нулю. Эта кривая называется кривой второго порядка. На самом деле может случиться, что нет вовсе точек
одновременно не равны нулю. Эта кривая называется кривой второго порядка. На самом деле может случиться, что нет вовсе точек  с действительными координатами, удовлетворяющих уравнению (1). В этом случае говорят, что уравнение (1) определяет мнимую кривую второго порядка. Мы не будем изучать мнимые кривые. Уравнение
с действительными координатами, удовлетворяющих уравнению (1). В этом случае говорят, что уравнение (1) определяет мнимую кривую второго порядка. Мы не будем изучать мнимые кривые. Уравнение
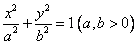
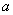 и
и  . В частности, при
. В частности, при  уравнение окружности
уравнение окружности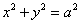
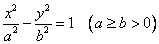

 .
.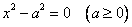 .
. .
.
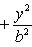

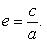
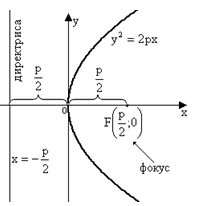 Уравнение:
Уравнение:  (1) Ось симметрии параболы – ось Ox
(1) Ось симметрии параболы – ось Ox
 Уравнение:
Уравнение: 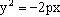 (2) Ось симметрии параболы – ось Ox
(2) Ось симметрии параболы – ось Ox
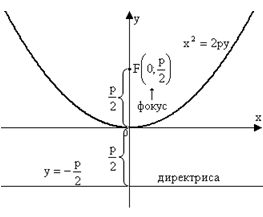 Уравнение:
Уравнение:  (3) Ось симметрии параболы – ось Oy
(3) Ось симметрии параболы – ось Oy
 Уравнение:
Уравнение: 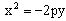 (4) Ось симметрии параболы – ось Oy
(4) Ось симметрии параболы – ось Oy
 a > 0, b > 0, называется эллиптическим параболоидом.
a > 0, b > 0, называется эллиптическим параболоидом. a > 0, b > 0, c > 0, называется однополостным гиперболоидом.
a > 0, b > 0, c > 0, называется однополостным гиперболоидом.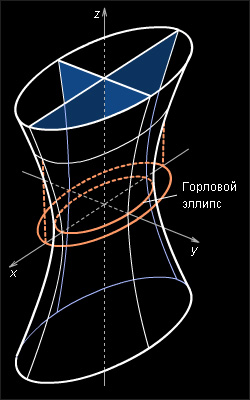
 называется цилиндрической поверхностью с образующей
называется цилиндрической поверхностью с образующей  , если для любой точки
, если для любой точки 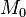 этой поверхности прямая, проходящая через эту точку параллельно образующей
этой поверхности прямая, проходящая через эту точку параллельно образующей 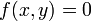 , то
, то  .
. , называется направляющей цилиндрической поверхности.
, называется направляющей цилиндрической поверхности.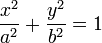



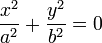




 , если для любой точки
, если для любой точки 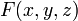 называется однородной порядка
называется однородной порядка  , если
, если  выполняется следующее:
выполняется следующее: 
 , где
, где 
 и т. п.
и т. п.
 служит множество всех чисел, кроме –3.
служит множество всех чисел, кроме –3.
 , где l 0 начальная длина стержня, а —
, где l 0 начальная длина стержня, а —  коэффициент линейного расширения. Указанная формула имеет смысл при любых значениях t. Однако, областью определения функции l=g (t) является промежуток в несколько десятков градусов, для которого справедлив закон линейного расширения.
коэффициент линейного расширения. Указанная формула имеет смысл при любых значениях t. Однако, областью определения функции l=g (t) является промежуток в несколько десятков градусов, для которого справедлив закон линейного расширения.
 .
Oчевидно, что из известных нам невозможных действий здесь может случиться деление на нуль. Найдем значения аргумента, при которых знаменатель обращается в нуль, и исключим их из области определения.
x 2–1=0; x 2=1; x 1=1; x 2= –1.
Областью определения этой функции служит множество всех чисел, кроме –1 и 1.
.
Oчевидно, что из известных нам невозможных действий здесь может случиться деление на нуль. Найдем значения аргумента, при которых знаменатель обращается в нуль, и исключим их из области определения.
x 2–1=0; x 2=1; x 1=1; x 2= –1.
Областью определения этой функции служит множество всех чисел, кроме –1 и 1.
 .
Выражение, находящееся под корнем, по определению арифметического квадратного корня должно быть неотрицательным. Составим и решим неравенство:
.
Выражение, находящееся под корнем, по определению арифметического квадратного корня должно быть неотрицательным. Составим и решим неравенство:
 Областью определения этой функции служит множество чисел, не меньших –5.
Областью определения этой функции служит множество чисел, не меньших –5.


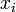 (
(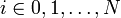 ) из некоторой области
) из некоторой области  . Пусть значения функции
. Пусть значения функции  известны только в этих точках:
известны только в этих точках: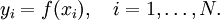
 из заданного класса функций, что
из заданного класса функций, что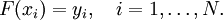
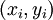 называют точками данных или базовыми точками.
называют точками данных или базовыми точками. — шагом интерполяционной сетки. Он может быть как переменным, так и постоянным.
— шагом интерполяционной сетки. Он может быть как переменным, так и постоянным. — интерполирующей функцией или интерполянтом.
— интерполирующей функцией или интерполянтом.
 Свойства:
Свойства:  = [
= [  )
)  = [
= [ 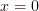
 (
( 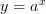 , где a > 1
, где a > 1 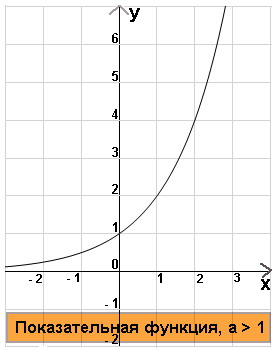 Свойства:
Свойства:  )
)  Свойства:
Свойства:  , a > 1
, a > 1  )
)  )
)
 Свойства:
Свойства:  ]
] ], где
], где 
 ], где
], где 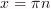 , где
, где  ], где
], где 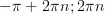 ], где
], где 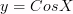
 Свойства:
Свойства:  , где
, где 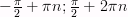 ], где
], где  можно рассматривать как композицию функций
можно рассматривать как композицию функций
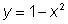 и
и  .
.
 . Например, запись
. Например, запись  означает,
что функция h получена как композиция функций f и g (сначала применяется g, а затем f),
т. е.
означает,
что функция h получена как композиция функций f и g (сначала применяется g, а затем f),
т. е.  . Операция образования сложной функции (или композиция функций) не обладает переместительным свойством:
. Операция образования сложной функции (или композиция функций) не обладает переместительным свойством:
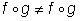 . Чтобы можно было вычислить сложную функцию h = f(g(x)), надо, чтобы число g(x), т. е. значение функции g,
попадало в область определения функции f.
. Чтобы можно было вычислить сложную функцию h = f(g(x)), надо, чтобы число g(x), т. е. значение функции g,
попадало в область определения функции f.
 ,
т. е. те, для которых число
,
т. е. те, для которых число  попадает в область определения функции
попадает в область определения функции 
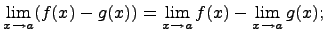



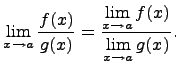

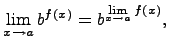
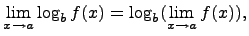
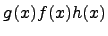 для всех x близких к a, за исключением, быть может, самой точки x = a. Тогда, если
для всех x близких к a, за исключением, быть может, самой точки x = a. Тогда, если