
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метрические задачи на прямую и плоскостьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1 Составить уравнение плоскости, проходящей через начало координат, параллельной прямой 2 Составить уравнение плоскости, проходящей через точку М (-1; 1; 3), параллельной прямой 3 Составить уравнения проекции прямой на плоскость П: 4 Найти расстояние от точки Р (7; 9; 7) до прямой 5 Найти расстояние между скрещивающимися прямыми: 6 Даны две прямые: а) Доказать, что они скрещиваются. б) Написать уравнения плоскостей, проходящих через каждую из них параллельно второй прямой. в) Найти расстояние между скрещивающимися прямыми и между плоскостями; убедиться в том, что эти расстояния равны. 7 Найти угол между прямой 8 Найти угол между следующими прямыми Определить угол между прямой 9 Вычислить расстояние от точки Р (1; -1; -2) до прямой 10 Убедившись, что прямые 11 Вычислить кратчайшее расстояние между двумя прямыми в каждом из следующих случаев: а) б) в)
Тема 5 Алгебраические линии и поверхности второго порядка Теоретические вопросы 1 Дать определение окружности и записать ее уравнения. Как в каждом случае найти центр и радиус окружности? 2 Что называется степенью точки относительно окружности? Каков геометрический смысл степени точки? 3 Что называется радикальной осью двух окружностей? Радикальным центром? 4 Сформулировать геометрические и алгебраические определения эллипса, гиперболы, параболы. Записать канонические уравнения. 5 Основные элементы линий: фокальные радиусы, эксцентриситет, дирекориса, фокуса, асимптоты гиперболы. 6 Равносторонняя гипербола. Сопряженные гиперболы, параболы. 7 Директориальное свойство эллипса, гиперболы, параболы. Теорема Аполлония. 8 Построение эллипса, гиперболы, параболы. 9 Общее уравнение линии второго порядка. 10 Схема приведения общего уравнения линии второго порядка к каноническому виду. 11 Определение поверхности второго порядка. Уравнения. 12 Канонические уравнения поверхностей второго порядка. Классификация. а) Центральные квадрики: эллипсоиды; гиперболоиды; конусы. б) Нецентральные квадрики: параболоиды; цилиндры; квадрики, распавшиеся на две плоскости.
13 Линейчатые поверхности второго порядка и их прямолинейные образующие. 14 Поверхности вращения.
Задачи Окружность. Эллипс 1 В прямоугольной декартовой системе координат даны уравнения: а) г) д) Выяснить, какие из уравнений определяют окружность. Найти координаты центра и радиус каждой. 2 Определить расположение точки М (2; 7) относительно окружности 3 Найти уравнение окружности, проходящей через три точки: а) А (4; 6), В (-2; -2), С (-2; 6); б) А (1; -4), В (4; 5), С (3; -2). 4 Составить уравнение окружности с центром в точке С (5; 2), касающейся прямой 5 Найти уравнение множества точек, для каждой из которых сумма квадратов расстояний от двух точек А (-1; 2) и В (1; 4) есть величина постоянная, равная 22. 6 Найти множество точек плоскости, имеющих одну и ту же степень относительно данной окружности. 7 Доказать, что радикальная ось двух окружностей есть прямая, перпендикулярная к линии центов. 8 Найти длины полуосей и координаты фокусов: а) 9 Найти точки, принадлежащие эллипсу а) 2; б) 3; в) 1. 10 Длина большой полуоси эллипса равна 6, эксцентриситет - 11 Составить каноническое уравнение эллипса, если: а) координаты вершин эллипса - б) фокальное расстояние равно 10; малая полуось – 5; в) расстояние между фокусами равно 8, а эксцентриситет - г) эллипс проходит через точку М (-3; 12 Написать уравнение директрис эллипса 13 Составить уравнение эллипса, зная, что: а) расстояние между директрисами равно 12, а большая ось равна б) директрисы заданы уравнениями х = 12 и х = - 12, а а эксцентриситет равен 14 Найти эксцентриситет эллипса, зная, что расстояние между его директрисами в 4 раза больше расстояния между фокусами. 15 На эллипсе, определяемом уравнением 16 Эллипс проходит через две противоположные вершины квадрата ABCD, и его фокусами являются две другие вершины этого квадрата. Написать каноническое уравнение эллипса и уравнение его директрис, если АС = 2 М.
17 Найти длины полуосей и координаты фокусов гипербол: а) б) Гипербола, парабола 1 Составить каноническое уравнение гиперболы по следующим данным: а) расстояние между вершинами равно 8, а расстояние между фокусами равно 10; б) длина действительной оси равна 6, гипербола проходит через точку М (9; 4); в) расстояние между фокусами 6, эксцентриситет равен 1,5; г) уравнения асимптот д) расстояние между директрисами равно е) эксцентриситет равен 1,5, расстояние между директрисами равно 2 Составить каноническое уравнение гиперболы, если угол между асимптотами равен 60º, а гипербола проходит через точку М (4 3 Составить уравнение гиперболы, имеющей общие фокусы с эллипсом 4 Дана гипербола 5 По данному эксцентриситету в каждом из случаев определить угол между асимптотами гиперболы: а) 6 Уравнения асимптот гиперболы 7 Составить уравнение гиперболы, эксцентриситет которой равен 3 и фокусы находятся в точках 8 Найти уравнение гиперболы, проходящей через точку М (-5; 3) и имеющей общие фокусы с равносторонней гиперболой 9 Определить координаты фокуса F и составить уравнение директрисы для каждой из парабол: а) б) 10 Составить каноническое уравнение параболы по следующим данным: а) р = 3; б) парабола проходит через точку Р (1; -4); в) директриса определяется уравнением х + 3 = 0; г) фокус имеет координаты (0; 5); д) директриса имеет уравнение у + 12 = 0. 11 Вычислить фокальный радиус точки М параболы 12 На параболе 13 Составить уравнение параболы по следующим данным: а) парабола симметрична относительно оси ОУ, фокус помещается в точке F (0; 2), вершина совпадает с началом координат; б) вершина находится в начале координат, парабола расположена в нижней полуплоскости, симметрична оси ОУ и р = 0,6; в) фокус имеет координаты F(5; 0), а ось ординат служит директрисой; г) парабола симметрична относительно оси ОУ и проходит через начало координат; прямая у = 2 пересекает параболу в точках с абсциссами 3 и -3. 14 Арка моста имеет форму параболы. Определить параметр параболы, зная, что пролет арок равен 24 м, а высота - 6 м. 15 Струя воды, выбрасываемая фонтаном, принимает форму параболы, параметр которой р = 0,1. Определить высоту струи, если известно, что она падает в бассейн на расстоянии 2 м от места выхода. 16 Эксцентриситет эллипса равен 17 Составить каноническое уравнение гиперболы, если уравнения директрис 18 Эксцентриситет гиперболы равен 2, фокальный радиус ее точки М равен 16. Найти расстояние от точки М до соответствующей этому фокусу директрисы.
|
||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.21.68 (0.01 с.) |

 и перпендикулярной к плоскости
и перпендикулярной к плоскости  .
.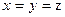 и перпендикулярной к плоскости
и перпендикулярной к плоскости  .
. ;
; .
.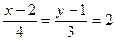 .
. и
и  .
. и
и  .
. и плоскостью
и плоскостью  .
. и
и  .
. и плоскостью П:
и плоскостью П:  .
. .
. и
и  параллельны, вычислить расстояние между ними.
параллельны, вычислить расстояние между ними.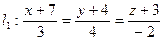 ;
;  ;
; ;
;  ;
; ;
;  .
. ; б)
; б)  ; в)
; в)  ;
; ;
;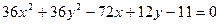 .
. .
.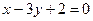 .
. ; б)
; б)  .
. абсциссы которых равны:
абсциссы которых равны: , а расстояние точки М эллипса до фокуса
, а расстояние точки М эллипса до фокуса 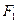 равно 7. Найти расстояние
равно 7. Найти расстояние  и координаты точки М.
и координаты точки М. ,
,  ,
,  ,
,  ;
; ) и расстояние между фокусами равно 6.
) и расстояние между фокусами равно 6. и найти расстояние между ними.
и найти расстояние между ними. ;
; .
. , найти точки, расстояние от которых до правого фокуса в 4 раза больше расстояния до левого фокуса.
, найти точки, расстояние от которых до правого фокуса в 4 раза больше расстояния до левого фокуса. ;
; .
. , а расстояние между фокусами равно 20;
, а расстояние между фокусами равно 20; , расстояние между фокусами равно 26;
, расстояние между фокусами равно 26; .
. ; 2).
; 2). и проходящей через точку М (4
и проходящей через точку М (4  ; 3).
; 3). . Написать уравнение сопряженной с ней гиперболы; найти эксцентриситеты и асимптоты данной и сопряженной гипербол.
. Написать уравнение сопряженной с ней гиперболы; найти эксцентриситеты и асимптоты данной и сопряженной гипербол. ; б)
; б)  .
. . Найти эксцентриситет.
. Найти эксцентриситет. и
и  .
. .
. ; в)
; в)  ;
; ; г)
; г) 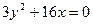 .
. , если ее абсцисса равна 8.
, если ее абсцисса равна 8. найти точку, фокальный радиус которой равен 9.
найти точку, фокальный радиус которой равен 9. , расстояние от точки, взятой на гиперболе до фокуса, в два раза больше расстояния от этой точки до соответствующей директрисы.
, расстояние от точки, взятой на гиперболе до фокуса, в два раза больше расстояния от этой точки до соответствующей директрисы.


