Гармоническая четверка точек. Сложное отношение четырех точек

1 С – середина отрезка АВ на евклидовой плоскости, D – середина ВС. Найти двойные отношения (), (), ().

2 Пользуясь одной линейкой, построить точку D, четвертую гармоническую к точкам А, В, и С в следующих трех случаях:

а) () = - 1; б) () = - 1; в) () = - 1.

Указание. Воспользоваться гармоническими свойствами полного четырехвершинника.

3 На евклидовой плоскости даны две параллельные прямые и отрезок на одной из них. Пользуясь одной линейкой, разделите этот отрезок пополам.

4 Какая прямая на евклидовой плоскости будет четвертой гармонической к трем прямым пучка , если прямая делит угол, образованный прямыми и , пополам?

5 На евклидовой плоскости даны три прямые пучка . Пользуясь одной линейкой,, построить четвертую гармоническую прямую к прямым

= - 1.

Указание. 1) Используйте принцип двойственности; 2) постройте А, В, С – точки пересечения прямых с какой либо прямой. Затем постройте точку D такую, что () = - 1, и прямую .

6 На евклидовой плоскости даны прямые одного пучка , причем перпендикулярна . Пользуясь одной линейкой, удвойте угол, образованный прямыми и .

Указание. Искомая прямая удовлетворяет условию = - 1.

7 На евклидовой плоскости дан отрезок АВ и его середина С. Пользуясь одной линейкой, проведите прямую через данную точку параллельно прямой АВ.

Указание. Постройте полный четырехвершинник так, чтобы , , . Тогда - искомая прямая.

8 На евклидовой плоскости даны две параллельные прямые и на одной из них отрезок АВ. Пользуясь одной линейкой, удвойте отрезок АВ.

Указание. Если - несобственная точка данных параллельных прямых, а Х – искомая точка, то = - 1.

9 На евклидовой плоскости дан параллелограмм. Пользуясь одной линейкой, через точку пересечения его диагоналей проведите прямые, параллельные его сторонам.

10 На прямой даны точки А, В, С. Постройте точку такую, чтобы () = 2.

11 Двойное отношение () равно -1. Найдите ().

12 а) Дано () = 3. Найдите ().

б) Дано () = - 2. Найдите (), (), (), (), ().

в) Дано () = - 1. Найдите (), (), (), (), ().

13 На евклидовой прямой даны фундаментальные точки , , проективной системы координат. Постройте точки А (1; -1), В (2; -1), С (3; 2).

Указание. Рассмотрите пучок прямых с центром в произвольной точке , не принадлежащей данной прямой, и аффинную систему координат с началом , базисные векторы и которой соответственны параллельны прямым и , причем + = . Затем постройте вектор . Искомой точкой будет точка пересечения данной прямой и прямой пучка с направляющим вектором .

14 Найдите двойное отношение () следующих четверок точек проективной прямой:

а) , , , ;

б) , , , ;

в) , , , .

 

15 Даны три точки и двойное отношение четверки точек проективной прямой. Найдите четвертую точку.

а) , , , . Найдите .

б) , , , . Найдите .

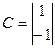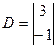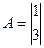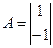в) , , , . Найдите .