
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7.2 Элементы проективной геометрииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопросы по теории 1 Аксиоматическое определение проективной плоскости 2 Модели проективной плоскости (доказательство непротиворечивости системы аксиом). 3 Принцип двойственности. Примеры. 4 Теорема Дезарга и ее частные случаи. 5 Гармоническая четверка точек. Построение четвертой гармонической точки. 6 Сложное отношение четырех точек. 7 Квадрики на
Задачи Модели 1 В трехмерном евклидовом пространстве дана сфера. Под точкой множества М будем понимать две диаметрально противоположные точки этой сферы. Под прямой – множество пар диаметрально противоположных точек, лежащих на окружности большого круга. Доказать, что построенное множество является проективной плоскостью. Рассмотреть связку S прямых и плоскостей с центром в точке О, где О – центр данной сферы, и постройте отображение а) образом точки б) образом прямой Показать, что 2 Какие из следующих предложений справедливы на проективной плоскости и какие – на евклидовой плоскости: а) существует одна и только одна прямая, инцидентная двум различным точкам; б) существует одна и только одна точка, инцидентная двум различным прямым. 3 Какие из нижеприведенных предложений справедливы в трехмерном проективном пространстве и какие – в евклидовом пространстве: а) существует одна и только одна прямая, инцидентная двум различным точкам; б) существует одна и только одна точка, инцидентная двум различным прямым; в) существует одна и только одна прямая, инцидентная двум различным плоскостям; г) три различные плоскости имеют по крайней мере одну общую точку; д) три различные прямые, не лежащие в одной плоскости, но попарно пересекающиеся, имеют одну и только одну общую точку; е) три различные прямые, попарно не скрещивающиеся и не проходящие через одну общую точку, лежат в одной плоскости? Замечание. Под проективной плоскостью трехмерного проективного пространства мы понимаем
4 Объяснить, почему в геометрии проективной плоскости не рассматриваются такие понятия, как «параллельность прямых», «перпендикулярность прямых», «биссектриса угла», «середина отрезка», «квадрат», «трапеция».
Теорема Дезарга 1 Рассмотреть частные случаи конфигурации Дезарга на расширенной плоскости, когда: а) дезаргова ось – несобственная прямая; б) дезаргов центр – несобственная точка. Сформулировать соответствующие частные случаи прямой и обратной теорем Дезарга в терминах евклидовой геометрии. 2 Проверьте, что для любой прямой из конфигурации Дезарга можно подобрать такие два трехвершинника этой же конфигурации, для которых данная прямая будет дезарговой осью. 3 На евклидовой плоскости трапеция вписана в четырехугольник так, что ее параллельные стороны параллельны одной из его диагоналей. Докажите, что непараллельные стороны трапеции пересекаются на другой диагонали. 4 На евклидовой плоскости вершины параллелограмма 5 Используя теорему Дезарга, докажите, что медианы треугольника пересекаются в одной точке. 6 На евклидовой плоскости даны параллельные прямые 7 Точку пересечения двух прямых
|
|||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.20.239 (0.006 с.) |

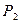 .
. определяемое следующими условиями:
определяемое следующими условиями: является прямая
является прямая  связки S;
связки S; является плоскость
является плоскость  , содержащая прямую
, содержащая прямую  .
. - биективное отображение, сохраняющее инцидентность.
- биективное отображение, сохраняющее инцидентность. , где
, где  - трехмерное векторное подпространство четырехмерного векторного пространства
- трехмерное векторное подпространство четырехмерного векторного пространства  .
.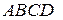 лежат на сторонах параллелограмма
лежат на сторонах параллелограмма  так, что
так, что 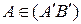 ,
,  ,
,  ,
, 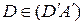 . докажите, используя теорему Дезарга, что центр симметрии параллелограмма ABCD совпадает с центром симметрии параллелограмма
. докажите, используя теорему Дезарга, что центр симметрии параллелограмма ABCD совпадает с центром симметрии параллелограмма  и
и  и точка Р, им не принадлежащая. Пользуясь одной линейкой, через точку Р проведите прямую, параллельную прямым
и точка Р, им не принадлежащая. Пользуясь одной линейкой, через точку Р проведите прямую, параллельную прямым  и
и  будем называть недоступной, если эти прямые пересекаются за пределами чертежа. Пользуясь одной линейкой, проведите прямую через точку N и недоступную точку пересечения прямых
будем называть недоступной, если эти прямые пересекаются за пределами чертежа. Пользуясь одной линейкой, проведите прямую через точку N и недоступную точку пересечения прямых 


