
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция, Как ее слушать и записыватьСодержание книги
Поиск на нашем сайте
Геометрия Материалы для практических занятий по дисциплинам «Аналитическая геометрия» и «Геометрия» для студентов направлений 010100 «Математика» и 050100 «Педагогическое образование», профиль «Математическое образование»
Курган 2013
Кафедра алгебры, геометрии и методики преподавания математики
Дисциплина: «Геометрия», «Аналитическая геометрия» (направления 010100 «Математика», 050100 «Педагогическое образование», профиль «Математическое образование») Составили: старший преподаватель С. В. Бреславец старший преподаватель С. М. Коростелева
Утверждены на заседании кафедры «13» декабря 2012 г. Рекомендованы методическим советом университета «9» апреля 2013 г.
содержание Методические советы студентам-первокурсникам……………………......4 Тема 1 Элементы векторной алгебры на плоскости и в пространстве......5 Тема 2 Метод координат на плоскости и в пространстве………………..9 Тема 3 Прямая линия на плоскости………………………………………..13 Тема 4 Плоскость и прямая в пространстве……………………………….19 Тема 5 Алгебраические линии и поверхности второго порядка…………27 Тема 6 Геометрические преобразования на плоскости…………………..34 Тема 7.1 Элементы конструктивной геометрии. Методы изображений…36 Тема 7.2 Элементы проективной геометрии……………………………….42 Список литературы……………………………………………………..…….47 МЕТОДИЧЕСКИЕ СОВЕТЫ СТУДЕНТАМ-ПЕРВОКУРСНИКАМ
Лекция, как ее слушать и записывать 1 Лекция – основной вид обучения в вузе. 2 На лекции излагаются основные положения теории, ее понятия и законы, приводятся факты, показывающие связь теории с практикой. 3 Накануне лекции необходимо повторить содержание предыдущей, а затем посмотреть тему очередной лекции по программе. 4 Полезно вести запись лекций, для непонятных вопросов оставлять место, которое будет заполнено, но уже вне аудитории при работе над темой лекции с учебными пособиями. 5 Записи лекций следует вести в отдельной тетради, оставляя место для дополнений во время самостоятельной работы над темой каждой лекции. 6 При конспектировании лекций выделяйте главы и разделы, параграфы, подчеркивайте основное.
Практическое занятие, как к нему готовиться 1 Практическое занятие – наиболее активный вид учебных занятий в вузе. Он предполагает самостоятельную работу над лекциями и учебными пособиями. 2 Назначение практических занятий по геометрии – научить студентов методам решения геометрических задач, сформировать у них навыки самостоятельного применения изученной теории в курсе геометрии, закрепить эту теорию. 3 К каждому практическому занятию нужно готовиться. Подготовку следует начинать с повторения теории (по записям в конспекте или по учебному пособию). После этого нужно решить задачи из предложенного домашнего задания.
Организация самостоятельной работы 1 Бюджет времени студента определяется временем, отведенным на занятия по расписанию и на самостоятельную работу. Задание и материал для самостоятельной работы даются во время учебных занятий, на этих же занятиях преподаватель осуществляет контроль за самостоятельной работой. 2 Для выполнения всего объема самостоятельной работы необходимо заниматься в среднем 4 часа ежедневно, то есть по 24 часа в неделю. На самостоятельную работу по геометрии еженедельно следует расходовать по 3 – 4 часа. 3 Начинать самостоятельные занятия следует в первые же дни семестра, установить определенный порядок, равномерный ритм на весь семестр. Полезно для этого составить расписание порядка дня.
Окружность. Эллипс 1 В прямоугольной декартовой системе координат даны уравнения: а) г) д) Выяснить, какие из уравнений определяют окружность. Найти координаты центра и радиус каждой. 2 Определить расположение точки М (2; 7) относительно окружности 3 Найти уравнение окружности, проходящей через три точки: а) А (4; 6), В (-2; -2), С (-2; 6); б) А (1; -4), В (4; 5), С (3; -2). 4 Составить уравнение окружности с центром в точке С (5; 2), касающейся прямой 5 Найти уравнение множества точек, для каждой из которых сумма квадратов расстояний от двух точек А (-1; 2) и В (1; 4) есть величина постоянная, равная 22. 6 Найти множество точек плоскости, имеющих одну и ту же степень относительно данной окружности. 7 Доказать, что радикальная ось двух окружностей есть прямая, перпендикулярная к линии центов. 8 Найти длины полуосей и координаты фокусов: а) 9 Найти точки, принадлежащие эллипсу а) 2; б) 3; в) 1. 10 Длина большой полуоси эллипса равна 6, эксцентриситет - 11 Составить каноническое уравнение эллипса, если: а) координаты вершин эллипса - б) фокальное расстояние равно 10; малая полуось – 5; в) расстояние между фокусами равно 8, а эксцентриситет - г) эллипс проходит через точку М (-3; 12 Написать уравнение директрис эллипса 13 Составить уравнение эллипса, зная, что: а) расстояние между директрисами равно 12, а большая ось равна б) директрисы заданы уравнениями х = 12 и х = - 12, а а эксцентриситет равен 14 Найти эксцентриситет эллипса, зная, что расстояние между его директрисами в 4 раза больше расстояния между фокусами. 15 На эллипсе, определяемом уравнением 16 Эллипс проходит через две противоположные вершины квадрата ABCD, и его фокусами являются две другие вершины этого квадрата. Написать каноническое уравнение эллипса и уравнение его директрис, если АС = 2 М. 17 Найти длины полуосей и координаты фокусов гипербол: а) б) Гипербола, парабола 1 Составить каноническое уравнение гиперболы по следующим данным: а) расстояние между вершинами равно 8, а расстояние между фокусами равно 10; б) длина действительной оси равна 6, гипербола проходит через точку М (9; 4); в) расстояние между фокусами 6, эксцентриситет равен 1,5; г) уравнения асимптот д) расстояние между директрисами равно е) эксцентриситет равен 1,5, расстояние между директрисами равно 2 Составить каноническое уравнение гиперболы, если угол между асимптотами равен 60º, а гипербола проходит через точку М (4 3 Составить уравнение гиперболы, имеющей общие фокусы с эллипсом 4 Дана гипербола 5 По данному эксцентриситету в каждом из случаев определить угол между асимптотами гиперболы: а) 6 Уравнения асимптот гиперболы 7 Составить уравнение гиперболы, эксцентриситет которой равен 3 и фокусы находятся в точках 8 Найти уравнение гиперболы, проходящей через точку М (-5; 3) и имеющей общие фокусы с равносторонней гиперболой 9 Определить координаты фокуса F и составить уравнение директрисы для каждой из парабол: а) б) 10 Составить каноническое уравнение параболы по следующим данным: а) р = 3; б) парабола проходит через точку Р (1; -4); в) директриса определяется уравнением х + 3 = 0; г) фокус имеет координаты (0; 5); д) директриса имеет уравнение у + 12 = 0. 11 Вычислить фокальный радиус точки М параболы 12 На параболе 13 Составить уравнение параболы по следующим данным: а) парабола симметрична относительно оси ОУ, фокус помещается в точке F (0; 2), вершина совпадает с началом координат; б) вершина находится в начале координат, парабола расположена в нижней полуплоскости, симметрична оси ОУ и р = 0,6; в) фокус имеет координаты F(5; 0), а ось ординат служит директрисой; г) парабола симметрична относительно оси ОУ и проходит через начало координат; прямая у = 2 пересекает параболу в точках с абсциссами 3 и -3. 14 Арка моста имеет форму параболы. Определить параметр параболы, зная, что пролет арок равен 24 м, а высота - 6 м. 15 Струя воды, выбрасываемая фонтаном, принимает форму параболы, параметр которой р = 0,1. Определить высоту струи, если известно, что она падает в бассейн на расстоянии 2 м от места выхода. 16 Эксцентриситет эллипса равен 17 Составить каноническое уравнение гиперболы, если уравнения директрис 18 Эксцентриситет гиперболы равен 2, фокальный радиус ее точки М равен 16. Найти расстояние от точки М до соответствующей этому фокусу директрисы.
Сфера. Эллипсоид 1 Составить уравнение сферы с центром в точке О и радиусом R, если О (2; -1; 3), R = 5. 2 Составить уравнение сферы с центром S (-4; 0; 3), если точка М (-1; 4; 3) принадлежит сфере. Найдите расстояние от центра сферы до плоскости OYZ и до оси ОХ. 3 Написать уравнение сферы, если: а) центр сферы О (0; 0; 0) и точка М (6; -2; 3) принадлежит сфере; б) центр сферы S (1; 4; -7) и сфера касается плоскости 4 Найти центр и радиус окружности: 5 Два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найдите длину линии, по которой пересекаются их поверхности. 6 Исследовать методом сечений поверхность второго порядка, заданную в прямоугольной декартовой системе координат уравнением 7 Исследовать методом сечений поверхность второго порядка, заданную в прямоугольной декартовой системе координат уравнением 8 Написать уравнение эллипсоида, оси которого совпадают с осями координат, который пересекает плоскость OYZ по эллипсу М (1; 9 Исследовать методом сечений поверхность второго порядка, заданную в прямоугольной декартовой системе координат уравнением: а) б) 10 Найти сечение эллипсоида
Гиперболоиды, параболоиды 1 Написать каноническое уравнение однополостного гиперболоида, если поверхность проходит через точку ( 2 Провести исследование поверхности второго порядка, заданной в прямоугольной декартовой системе координат уравнением 3 Провести исследование поверхности второго порядка, заданной в прямоугольной декартовой системе координат уравнением 4 Построить сечения координатными плоскостями поверхностей, заданных следующими уравнениями: а) 5 Составить уравнение поверхности, образованной вращением гиперболы с полуосями 2 и 4 ее мнимой оси, совпадающей с осью OZ. Центр гиперболы совпадает с началом координат. Гипербола лежит в плоскости XOZ. Сделать чертеж. 6 Написать каноническое уравнение однополостного гиперболоида, если поверхность пересекает плоскость OXY по окружности 7 Определить вид и провести исследование поверхности второго порядка, заданной уравнением 8 Определить вид и провести исследование поверхности второго порядка, заданной уравнением 9 Исследовать методом сечений поверхность второго порядка, заданную в прямоугольной декартовой системе координат уравнением 11 Исследовать методом сечений поверхность второго порядка, заданную в прямоугольной декартовой системе координат уравнением 12 Построить сечения координатными плоскостями поверхностей, заданных следующими уравнениями: а)
13 Сделать чертеж в прямоугольной декартовой системе координат поверхности, заданной уравнением 14 Исследовать методом сечений поверхность второго порядка, заданную в прямоугольной декартовой системе координат уравнением Метод движений а) задачи на доказательства 1 На высоте ВД треугольника АСВ взята точка К так, что АК = КС. Доказать, что треугольник АВС равнобедренный. 2 Построить квадрат, две противоположные вершины которого лежали бы на данной прямой, а две другие – на данных окружностях. 3 На стороне АВ параллелограмма АВСД, вне его, построен квадрат АВМК, а на стороне СД в той же полуплоскости, что и параллелограмм, построен квадрат СДРЕ. Доказать, что расстояние между центрами квадратов равно стороне параллелограмма. 4 Две прямые, содержащие точку пересечения диагоналей параллелограмма, пересекают его стороны соответственно в точках М и К, Р и Е. Доказать, что МРКЕ – параллелограмм. 5 Две равные окружности пересекаются в точках А и В. Через Точку А проведена хорда МА одной окружности, а через точку В – хорда ВК другой окружности, причем МА и ВК параллельны. Доказать, что эти хорды равны. 6 Дан правильный шестиугольник ABCDEF, М – середина диагонали АС, N – середина стороны DE. Доказать, что треугольник MNF – правильный. 7 Через центр правильного треугольника проведены две прямые, угол между которыми равен 600. Доказать, что отрезки этих прямых, которые являются их пересечением с треугольником, равны. б) задачи на построение и вычисление 1 На данной прямой построить такую точку, чтобы сумма расстояний от этой точки до двух данных точек, не лежащих на этой прямой, была наименьшей. 2 Найти площадь трапеции, сумма оснований которой равна 21 см, а диагонали равны 13 см и 20 см. 3Даны две пересекающиеся прямые c и d и две точки А и В, не принадлежащие им. Построить параллелограмм АВСД так, чтобы вершины С и Д лежали соответственно на прямых c и d. 4 Построить биссектрису угла АОВ, вершина О которого не доступна. 5 Земельный участок квадратной формы был огорожен. От изгороди сохранились два столба на параллельных сторонах квадрата. Кроме того остался столб в центре участка. Построить границу участка. 6 Построить параллельные прямые а, b, с, проходящие соответственно через данные точки А, В, С так, чтобы одна из них была средней линией полосы, определяемой двумя другими прямыми. 7 Построить равнобедренный прямоугольный треугольник так, чтобы вершины его острых углов принадлежали данным окружностям, а вершиной прямого угла являлась данная точка. 8 На сторонах АВ и АС треугольника АВС, вне его построены квадраты ABMN и ACPQ. Найти длину отрезка NQ, если длина медианы АЕ треугольника АВС равна m. Метод преобразований 1 Доказать, что точка пересечения прямых, содержащих боковые стороны равнобедренной трапеции, точка пересечения ее диагоналей и середины оснований трапеции принадлежат одной прямой. 2 Через точку касания двух окружностей проведены две произвольные прямые, которые пересекают эти окружности в точках А, В и С, Д, причем А и В лежат на одной окружности, С и Д – на другой. Доказать, что АВ ׀׀ СД. 3 Даны две окружности и точка М. Построить на окружностях соответственно точки А и В, чтобы М Î АВ и АМ: МВ = 2: 3. 4 Построить равнобедренный треугольник, зная угол при его вершине и сумму длин основания и высоты. 5 Доказать, что отношение площади данного четырехугольника к площади четырехугольника, вершины которого находятся в серединах сторон данного, равно 2: 1. 6 Пользуясь только одной линейкой: а) построить середину отрезка, лежащего на одной из двух данных параллельных прямых; б) построить прямую, проходящую через данную точку М и параллельную двум данным параллельным прямым, не содержащим точку М. Алгебраический метод 1 Построить треугольник АВС, если даны высота BH и радиусы окружностей, описанных около треугольников АВН и СВН. 2 В данную окружность вписать прямоугольник, равновеликий данному квадрату. 3 Построить квадрат, площадь которого в два раза больше площади данного квадрата. 4 Построить круг, площадь которого равна площади кольца, между двумя концентрическими окружностями. 5 Построить квадрат, равновеликий данному треугольнику. 6 Построить прямоугольный треугольник по гипотенузе и биссектрисе прямого угла. Изображение плоских фигур 1 Построить изображение правильного шестиугольника различными способами.
2 Построить касательную к эллипсу: а) параллельную данной хорде, б) проходящую через данную на эллипсе точку.
3 Построить изображение правильного треугольника, вписанного в окружность и описанного около неё.
4 Построить изображения: а) прямоугольного треугольника; б) трапеции; в) равнобедренного треугольника; г) правильного шестиугольника, вписанных в окружность.
5 Построить изображения описанных около окружности: а) прямоугольного треугольника; б) равнобедренной трапеции; в) правильного шестиугольника.
6 Построить описанный около окружности равнобедренный прямоугольный треугольник.
7 Построить описанный около окружности ромб с острым углом в 60º.
8. Построить вписанную в окружность трапецию, основания которой видны из центра окружности под углами в 60º и 120º.
9 На изображении круга построить изображение: а) сектора с углом 15º; б) сегмента с дугой 75º; в) сектора с углом 135º; г) сегмента с дугой 135º; д) сектора с углом 75º.
Позиционные задачи 1 Построить точку пересечения плоскости, проходящей через ребро АД тетраэдра АВСД и точку М 2 Дано изображение треугольной пирамиды и её высоты. Через середину высоты и середину бокового ребра провести прямую и построить точку её пересечения с поверхностью пирамиды. 3 Точки E и F – середины рёбер ДС и ДА тетраэдра АВСД. Построить сечение тетраэдра плоскостью, проходящей через точку F, параллельно плоскости АВЕ (2 случая). 9 Построить сечение правильной четырёхугольной пирамиды плоскостью, проходящей через диагональ основания параллельно боковому ребру, противолежащему этой диагонали. 5 Построить сечение правильной пятиугольной призмы плоскостью, заданной тремя точками, произвольно выбранными на её боковых рёбрах, или на её боковых рёбрах и гранях. 6 Построить сечение правильной шестиугольной призмы плоскостью, заданной тремя точками, одна из которых выбрана на боковой грани, две другие – на боковых рёбрах. 7 Построить сечение параллелепипеда плоскостью, проходящей через три точки, лежащие на трёх попарно скрещивающихся рёбрах. 8 Построить сечение правильной пятиугольной пирамиды плоскостью, заданной тремя точками, одна из которых выбрана на ребре основания, две другие – на боковых рёбрах. 9 Построить сечение цилиндра плоскостью, заданной тремя точками на его боковой поверхности. 10 Построить сечение конуса плоскостью, заданной следом и точкой на боковой поверхности конуса. Метрические задачи 1 Дано изображение прямоугольного треугольника с отношением катетов 1:2. Построить изображение перпендикуляра, опущенного из вершины прямого угла на гипотенузу. 2 Трапеция А’B’C’D’ - изображение равнобедренной трапеции АВСД (АВ║СД), углы при основании которой равны 45º. Построить изображение центра окружности, описанной вокруг трапеции. 3 Дано изображение равнобедренного треугольника. Построить изображение: а) биссектрисы угла при вершине; б) перпендикуляра, опущенного из середины боковой стороны на основание; в) биссектрисы угла при основании. 4 Дано изображение треугольника и двух его высот. Построить изображение центра окружности, описанной около треугольника – оригинала. 5 Дано изображение прямоугольного треугольника с отношением катетов, равным 6 Построить изображение перпендикуляра, опущенного из вершины куба на его диагональ. 7 Дана правильная четырёхугольная пирамида SАВСД. Изобразить перпендикуляр, опущенный из точки Е грани SАВ на плоскость основания. 8 Дан прямоугольный параллелепипед АВСДА1В1С1Д1, рёбра которого относятся как 1:2:3. Построить изображение точки пересечения прямой С1С и биссектрисы угла ВВ1С1. 9 Длина ребра куба равна а. Найти площадь сечения, проведённого через диагональ АД1 грани АА1Д1Д и середину ребра ВВ1. 10 В правильной шестиугольной призме, у которой боковые грани – квадраты, провести плоскость через сторону нижнего основания и противолежащую ей сторону верхнего основания. Найти площадь сечения, если ребро призмы равно а. 11 АВСДА1В1С1Д1 – прямоугольный параллелепипед. АВ:АД:АА1=1:2:1. Через вершины В, С1, Д проведена плоскость. Точка P 12 Построить сечение правильного тетраэдра плоскостью, проходящей через: 1) ребро основания перпендикулярно противоположному боковому ребру; 2) через точку М 13 Дано изображение правильного тетраэдра SАВС. Построить изображение перпендикуляра, проведённого через точку P, лежащую на грани SАВ, к грани SВС. Аксонометрия. Метод Монжа 1 Построить изображение куба и правильной треугольной пирамиды в кабинетной проекции. 2 В правильной четырёхугольной пирамиде со стороной a и высотой h построить сечение, проходящее через сторону основания, перпендикулярно противоположной боковой грани. 3 Построить сечение правильной треугольной пирамиды, проходящее через ребро основания, перпендикулярно противоположному боковому ребру. Сторона основания равна a, высота h. 4 Построить изображение правильной четырёхугольной призмы, конуса, используя метод Монжа. 5 В правильный октаэдр, вписанный в сферу, вписать шар. 6 Построить изображение правильной четырёхугольной призмы и сечения, проходящего через вершину основания перпендикулярно противоположному боковому ребру, используя метод Монжа. Дополнительные задачи для самостоятельного решения
1 Дано изображение квадрата АВСД, М – середина АВ. Построить изображение перпендикуляра, опущенного из точки С на ДМ. 2 Дано изображение равнобедренного треугольника, высота которого равна основанию. Построить изображение центра окружности, описанной около треугольника – оригинала. 3 Построить изображение квадрата, вписанного в окружность и описанного около неё. 4 Построить изображение вписанных в окружность: а) прямоугольника, б) правильного восьмиугольника. 5 Построить изображение описанных около окружности: а) равнобедренного треугольника, б) ромба. 6 На изображении правильного шестиугольника построить изображения: а) апофемы, б) биссектрисы одного из внешних углов, в) перпендикуляра, проведённого через центр к одной из меньших диагоналей. 7 Изобразить правильный тетраэдр SАСВ и перпендикуляр, проведённый через точку P на его грани SАВ к грани SВС. 8 Дана правильная треугольная пирамида SАВС, О – центр основания АВС. Построить точку пересечения прямой SО с плоскостью, проходящей через ребро АВ и середину ребра SС. 9 В усечённый конус вписать правильную четырёхугольную призму. 10 В шар вписать цилиндр. 11 Построить изображение правильной шестиугольной призмы, описанной около шара. 12 Построить изображение правильной треугольной пирамиды, вписанной в шар. 13 Построить сечение правильной четырёхугольной пирамиды плоскостью, заданной тремя точками на боковых гранях. 14 Построить сечение куба АВСД 15 АВСДА1В1С1Д1 – параллелепипед, Е – середина ВВ1. Построить сечение параллелепипеда плоскостью, проходящей через точку Е, параллельно плоскости А1ВС1. 16 АВСД – правильный тетраэдр. ДМ – его высота, точка N – середина ДМ. Построить сечение тетраэдра плоскостью, проходящей через точку N, параллельно грани ДВС. 17 Построить сечение конуса плоскостью, проходящей через три точки на его боковой поверхности. 18 Дана правильная треугольная пирамида SАВС, О – центр основания АВС. Построить точку пересечения прямой OS с плоскостью, проходящей через ребро АВ и середину ребра SС. 19 Построить изображение правильной шестиугольной призмы в кабинетной проекции. 20 Высота правильной четырёхугольной призмы вдвое больше стороны её основания. 21 Построить плоскость, проходящую через вершину основания, перпендикулярно диагонали призмы, не проходящей через эту вершину. 22 В правильный тетраэдр, вписанный в сферу, вписать шар. 23 Построить изображение правильной треугольной пирамиды и сечения, проходящего через ребро основания перпендикулярно противоположному боковому ребру, используя метод Монжа. 24 Дано изображение куба. Построить изображение перпендикуляра, проведённого из вершины куба на любую его диагональ. 25 Изобразить правильный тетраэдр SABC и перпендикуляр, проведённый из точки P 26 Дано изображение куба АВСДА1В1С1Д1 и плоскость, проходящая через ребро А1В1 параллельно ребру СД и пересекающая АВСД. Точка P 27 АВСДА1В1С1Д1 – куб. Точка М
Вопросы по теории 1 Аксиоматическое определение проективной плоскости 2 Модели проективной плоскости (доказательство непротиворечивости системы аксиом). 3 Принцип двойственности. Примеры. 4 Теорема Дезарга и ее частные случаи. 5 Гармоническая четверка точек. Построение четвертой гармонической точки. 6 Сложное отношение четырех точек. 7 Квадрики на
Задачи Модели 1 В трехмерном евклидовом пространстве дана сфера. Под точкой множества М будем понимать две диаметрально противоположные точки этой сферы. Под прямой – множество пар диаметрально противоположных точек, лежащих на окружности большого круга. Доказать, что построенное множество является проективной плоскостью. Рассмотреть связку S прямых и плоскостей с центром в точке О, где О – центр данной сферы, и постройте отображение а) образом точки б) образом прямой Показать, что 2 Какие из следующих предложений справедливы на проективной плоскости и какие – на евклидовой плоскости: а) существует одна и только одна прямая, инцидентная двум различным точкам; б) существует одна и только одна точка, инцидентная двум различным прямым. 3 Какие из нижеприведенных предложений справедливы в трехмерном проективном пространстве и какие – в евклидовом пространстве: а) существует одна и только одна прямая, инцидентная двум различным точкам; б) существует одна и только одна точка, инцидентная двум различным прямым; в) существует одна и только одна прямая, инцидентная двум различным плоскостям; г) три различные плоскости имеют по крайней мере одну общую точку; д) три различные прямые, не лежащие в одной плоскости, но попарно пересекающиеся, имеют одну и только одну общую точку; е) три различные прямые, попарно не скрещивающиеся и не проходящие через одну общую точку, лежат в одной плоскости? Замечание. Под проективной плоскостью трехмерного проективного пространства мы понимаем 4 Объяснить, почему в геометрии проективной плоскости не рассматриваются такие понятия, как «параллельность прямых», «перпендикулярность прямых», «биссектриса угла», «середина отрезка», «квадрат», «трапеция».
Теорема Дезарга 1 Рассмотреть частные случаи конфигурации Дезарга на расширенной плоскости, когда: а) дезаргова ось – несобственная прямая; б) дезаргов центр – несобственная точка. Сформулировать соответствующие частные случаи прямой и обратной теорем Дезарга в терминах евклидовой геометрии. 2 Проверьте, что для любой прямой из конфигурации Дезарга можно подобрать такие два трехвершинника этой же конфигурации, для которых данная прямая будет дезарговой осью. 3 На евклидовой плоскости трапеция вписана в четырехугольник так, что ее параллельные стороны параллельны одной из его диагоналей. Докажите, что непараллельные стороны трапеции пересекаются на другой диагонали. 4 На евклидовой плоскости вершины параллелограмма 5 Используя теорему Дезарга, докажите, что медианы треугольника пересекаются в одной точке. 6 На евклидовой плоскости даны параллельные прямые 7 Точку пересечения двух прямых
Геометрия Материалы для практических занятий по дисциплинам «Аналитическая геометрия» и «Геометрия» для студентов направлений 010100 «Математика» и 050100 «Педагогическое образование», профиль «Математическое образование»
Курган 2013
Кафедра алгебры, геометрии и методики преподавания математики
Дисциплина: «Геометрия», «Аналитическая геометрия» (направления 010100 «Математика», 0501
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.72.52 (0.015 с.) |

 ; б)
; б)  ; в)
; в)  ;
; ;
;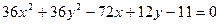 .
. .
.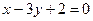 .
. ; б)
; б)  .
. абсциссы которых равны:
абсциссы которых равны: , а расстояние точки М эллипса до фокуса
, а расстояние точки М эллипса до фокуса 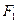 равно 7. Найти расстояние
равно 7. Найти расстояние  и координаты точки М.
и координаты точки М. ,
,  ,
,  ,
,  ;
; ) и расстояние между фокусами равно 6.
) и расстояние между фокусами равно 6. и найти расстояние между ними.
и найти расстояние между ними. ;
; .
. , найти точки, расстояние от которых до правого фокуса в 4 раза больше расстояния до левого фокуса.
, найти точки, расстояние от которых до правого фокуса в 4 раза больше расстояния до левого фокуса. ;
; .
. , а расстояние между фокусами равно 20;
, а расстояние между фокусами равно 20; , расстояние между фокусами равно 26;
, расстояние между фокусами равно 26; .
. ; 2).
; 2). и проходящей через точку М (4
и проходящей через точку М (4  ; 3).
; 3). . Написать уравнение сопряженной с ней гиперболы; найти эксцентриситеты и асимптоты данной и сопряженной гипербол.
. Написать уравнение сопряженной с ней гиперболы; найти эксцентриситеты и асимптоты данной и сопряженной гипербол. ; б)
; б)  .
. . Найти эксцентриситет.
. Найти эксцентриситет. и
и  .
. .
. ; в)
; в)  ;
; ; г)
; г) 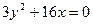 .
. , если ее абсцисса равна 8.
, если ее абсцисса равна 8. найти точку, фокальный радиус которой равен 9.
найти точку, фокальный радиус которой равен 9. , расстояние от точки, взятой на гиперболе до фокуса, в два раза больше расстояния от этой точки до соответствующей директрисы.
, расстояние от точки, взятой на гиперболе до фокуса, в два раза больше расстояния от этой точки до соответствующей директрисы. .
. .
. . Сделать чертеж.
. Сделать чертеж. . Выполнить чертеж.
. Выполнить чертеж. и проходит через точку
и проходит через точку ;
; .
. координатными плоскостями канонической системы координат. Выполнить чертеж.
координатными плоскостями канонической системы координат. Выполнить чертеж. ; 3; 2) и пересекает плоскость OXZ по гиперболе
; 3; 2) и пересекает плоскость OXZ по гиперболе  .
. . Сделать чертеж.
. Сделать чертеж. . Сделать чертеж.
. Сделать чертеж. ; б)
; б)  .
. , а плоскость OXZ по гиперболе
, а плоскость OXZ по гиперболе  .
. . Построить ее изображение.
. Построить ее изображение. . Построить изображение поверхности.
. Построить изображение поверхности. . Сделать чертеж.
. Сделать чертеж. . Сделать чертеж.
. Сделать чертеж. ; б)
; б)  .
. .
. . Сделать чертеж.
. Сделать чертеж. ВС, с прямой, заданной точками P
ВС, с прямой, заданной точками P  . Построить изображение центра окружности, вписанной в треугольник – оригинал.
. Построить изображение центра окружности, вписанной в треугольник – оригинал. , проходящее через точку А и середины рёбер
, проходящее через точку А и середины рёбер  и
и  .
.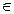 ASB к грани SBC.
ASB к грани SBC.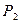 .
. определяемое следующими условиями:
определяемое следующими условиями: является прямая
является прямая  связки S;
связки S; является плоскость
является плоскость  , содержащая прямую
, содержащая прямую  .
. - биективное отображение, сохраняющее инцидентность.
- биективное отображение, сохраняющее инцидентность. , где
, где  - трехмерное векторное подпространство четырехмерного векторного пространства
- трехмерное векторное подпространство четырехмерного векторного пространства  .
.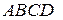 лежат на сторонах параллелограмма
лежат на сторонах параллелограмма  так, что
так, что 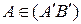 ,
,  ,
,  ,
, 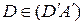 . докажите, используя теорему Дезарга, что центр симметрии параллелограмма ABCD совпадает с центром симметрии параллелограмма
. докажите, используя теорему Дезарга, что центр симметрии параллелограмма ABCD совпадает с центром симметрии параллелограмма  и
и  и точка Р, им не принадлежащая. Пользуясь одной линейкой, через точку Р проведите прямую, параллельную прямым
и точка Р, им не принадлежащая. Пользуясь одной линейкой, через точку Р проведите прямую, параллельную прямым  и
и 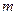 будем называть недоступной, если эти прямые пересекаются за пределами чертежа. Пользуясь одной линейкой, проведите прямую через точку N и недоступную точку пересечения прямых
будем называть недоступной, если эти прямые пересекаются за пределами чертежа. Пользуясь одной линейкой, проведите прямую через точку N и недоступную точку пересечения прямых 


