
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные виды уравнения плоскостиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Каждая плоскость в пространстве Охуz определяется линейным уравнением первой степени с тремя неизвестными.
образованную пересечением плоскостей А 1 х + В 1 у + С 1 z + D 1 = 0 и А 2 х + В 2 у + С 2 z + D 2 = 0 имеет вид:
(
Частные случая уравнения:
Ах + Ву + Cz = 0 (D = 0) – плоскость проходит через начало координат; Ах + Ву + D = 0 (C = 0) – плоскость параллельна оси Оz (аналогичный смысл имеют уравнения Ах + Cz + D = 0 и Ву + Cz + D = 0); Ах + Ву = 0 (D = C = 0) – плоскость проходит через ось Оz (Ах + Cz = 0, Ву + Cz = 0 – через ось Оу и Ох соответственно); Ах + D = 0 (В = С = 0) – плоскость параллельна плоскости Оуz (Cz + D = 0, Ву + D = 0 – параллельна плоскости Оxу и Оxz соответственно); Ах = 0, т.е. х = 0 (В = С = D = 0) – плоскость совпадает с плоскостью Оуz (y = 0, z = 0 – уравнения плоскостей Оxz и Оxy соответственно);
М 1(x 1; у 1; z 1), М 2(x 2; у 2; z 2), М 3(x 3; у 3; z 3):
где р – длина перпендикуляра, опущенного из начала координат на плоскость, α, β, γ – углы, образованные этим перпендикуляром с положительными направлениями осей Ох, Оу и Oz соответственно (cos2 α +cos2 β +cos2 γ = 1) Общее уравнение плоскости можно преобразовать в нормальное уравнение путем умножения на нормирующий множитель Пример 1. Построить плоскости, заданные уравнениями: 1) 2 у – 5 = 0; 2) x + z – 1 = 0; 3) 3 x + 4 y + 6 z – 12 = 0.
1). Плоскость 2 у – 5 = 0 параллельна плоскости Oxz; она отсекает на оси Оу отрезок, равный 2,5 и имеет вид, представленный на рис. 1.
2). Плоскость x + z – 1 = 0 параллельна оси Oу; она пересекает плоскость Оxz по прямой x + z = 1, отсекая на осях Оx и Оz отрезки, равные 1(рис.).
соответственно (рис. 3).
Рис.1. Рис.2. Рис.3. Задание для самостоятельного решения 1. Составить уравнение плоскости, проходящей через: а) точку М (-2, 3, 1) параллельно плоскости Оху; б) точку М и ось Оу. Построить эти плоскости.
2. Составить уравнение плоскости, проходящей через: а) точку A (5, - 4, 6) перпендикулярно оси Ох; б) точку А и отсекающей равные отрезки на координатных осях. Построить эти плоскости.
Пример 2. Уравнение плоскости 2 х – 6 у + 3 z – 14 = 0 привести к нормальному виду.
Задание для самостоятельного решения 1. Определить направляющие косинусы радиус – вектора, перпендикулярного к плоскости 3 х – 4 у + 5 z – 10 = 0.
Пример 3. Написать уравнение плоскости:
а) параллельной оси Oz и проходящей через точки М 1 (3, –1, 2) и М 2 (–1, 2, 5);
Ах + Ву + D =0, получаем
Задания для самостоятельного решения
Пример 5. Написать уравнение плоскости, проходящей через три заданные точки М 1 (1, 0, -1), М 2 (2, 2, 3), М 3 (0, -3, 1).
Задание для самостоятельного решения
1. Написать уравнение плоскости, проходящей через точки М 1 (- 2, 0, 0), М 2 (0, 4, 0), М 3 (0, 0, 5).
Задания для самостоятельного решения 1. Найти уравнение плоскости, проходящей через точку М (1, 1, 1) перпендикулярно линии пересечения двух плоскостей x – y + 2 z – 3 = 0 и 2 x – z + 4 = 0.
2. Найти уравнение плоскости, проходящей через линию пересечения двух плоскостей x – 2 y + 3 z – 4 = 0 и x + у – 5 z + 9 = 0 и параллельной оси Ох.
Угол между двумя плоскостями, условия параллельности и перпендикулярности двух плоскостей
Под углом между плоскостями понимается угол между нормальными векторами этих плоскостей.
Если плоскости Q 1 и Q 2 заданы уравнениями А 1 х + В 1 у + С 1 z + D 1 = 0 и А 2 х + В 2 у + С 2 z + D 2 = 0, нормальные вектора которых
cos φ =
Наименьший из двух смежных углов, образованных этими плоскостями, равен cos φ = Условие параллельности плоскостей Q 1 и Q 2: Условие перпендикулярности плоскостей Q 1 и Q 2: A 1 А 2 + B 1 B 2 + C 1 C 2 = 0. Плоскости совпадают, когда:
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 4012; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.244 (0.007 с.) |






 Уравнение плоскости, проходящей через точку
Уравнение плоскости, проходящей через точку

 М 0 (x 0; у 0; z 0)перпендикулярно вектору
М 0 (x 0; у 0; z 0)перпендикулярно вектору  = { A; B; С }:
= { A; B; С }:


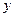

 А (х - x 0) + В (y - y 0) + C (z - z 0) = 0.
А (х - x 0) + В (y - y 0) + C (z - z 0) = 0.


 где λ – числовой множитель.
где λ – числовой множитель.
 Общее уравнение плоскости:
Общее уравнение плоскости: 

 Вектор
Вектор 


 Уравнение плоскости в отрезках:
Уравнение плоскости в отрезках:  = 1.
= 1. 



 а, b, с – длины отрезков (с учетом знаков), отсекаемых
а, b, с – длины отрезков (с учетом знаков), отсекаемых = 0.
= 0.
 ; знак берется противоположным знаку свободного члена D (в общем уравнении плоскости).
; знак берется противоположным знаку свободного члена D (в общем уравнении плоскости).
 Эта плоскость отсекает на осях Ох, Оу, Oz отрезки, равные 4, 3, 2
Эта плоскость отсекает на осях Ох, Оу, Oz отрезки, равные 4, 3, 2





 Подставляя найденные значения А и В в уравнение
Подставляя найденные значения А и В в уравнение Dx
Dx 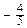 Dy + D =0. После сокращения на
Dy + D =0. После сокращения на  D получим 3 х + 4 у –5=0.
D получим 3 х + 4 у –5=0.






 решение,
решение, Далее, воспользовавшись способом, приведенным в
Далее, воспользовавшись способом, приведенным в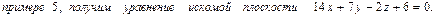
 = { A 1; B 1; С 1} и
= { A 1; B 1; С 1} и = { A 2; B 2; С 2}, то:
= { A 2; B 2; С 2}, то: .
. .
.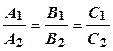 .
. .
.


