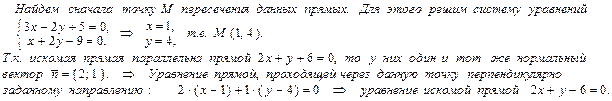Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, пересечение прямыхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Под углом между прямыми l 1 и l 2 плоскости понимается наименьший (острый) из двух смежных углов, образованных этими прямыми.
Если прямые заданы уравнениями с угловым коэф-
то угол φ между ними равен: tg φ = Условие параллельности прямых l 1 и l 2: k 1 = k 2 . Условие перпендикулярности прямых l 1 и l 2: k 1 = – Если прямые l 1 и l 2 заданы общими уравнениями А 1 х + В 1 у + С 1 = 0 и А 2 х + В 2 у + С 2 = 0, то угол φ между ними равен углу между их нормальными векторами
tg φ =
Условие параллельности прямых l 1 и l 2: Условие перпендикулярности прямых l 1 и l 2: A 1 А 2 + B 1 B 2 = 0.
Для нахождения общих точек прямых l 1 и l 2 необходимо решить систему уравнений
При этом: если если если Расстояние от данной точки до данной прямой
Расстоянием d от точки М 0 (x 0; у 0) до прямой Ах + Ву + С = 0 называется длина перпендикуляра, опущенного из этой точки на прямую: d =
Расстояние d от точки М 0 (x 0; у 0) до прямой х cos α + у sin α – p = 0:
d = | х 0cos α + у 0sin α – p |.
Пример 1. Найти угол между прямыми:
1) у = 2 х – 3 и у = 1¤2 х + 5; 2) 2 х – 3 у + 10 = 0 и 5 х – у + 4= 0; 3) у = 3¤4 х – 2 и 8 х + 6 у + 5 = 0. 1) Имеем: tg φ = 2) tg φ = 3) Здесь k 1 = у = – Можно воспользоваться формулой: tg φ = Задания для самостоятельного решения 1. Найти угол между прямыми: а) 3 х + 2 у – 1 = 0 и 5 х – у + 4 = 0; б) у = 3,5 х – 3 и 7 х – 2 у + 2= 0; в) х + 4 у + 10 = 0 и 5 у – 3= 0.
2. Исследовать взаимное расположение следующих пар прямых: а) 3 х + 5 у – 9 = 0 и 10 х – 6 у + 4 = 0; б) 2 у = х – 1 и 4 у – 2 х + 2= 0; в) х + у = 0 и х – у = 0; г) 2 х + 3 у = 8 и х + у – 3 = 0.
Пример 2. Через точку пересечения 3 х – 2 у + 5 = 0, х + 2 у – 9= 0 проведена прямая, параллельная прямой 2 х + у + 6 = 0. Составить ее уравнение. Задания для самостоятельного решения 1. Найти уравнение прямой, проходящей через точку А (-1, 2): а) параллельно прямой у = 2 х – 7; б) перпендикулярно прямой х + 3 у - 2 = 0.
2. Найти уравнение прямой, проходящей через точку В (2, -3): а) параллельно прямой, соединяющей точки М 1 (- 4, 0) и М 2 (2, 2); б) перпендикулярно прямой х – у = 0.
Пример 3. Найти координаты точки М 2, симметричной точке М 1 (- 3, 4) относительно прямой 4 х – у – 1 = 0.
Задания для самостоятельного решения 1. Точка А (2, -5) является вершиной квадрата, одна из сторон которого лежит на прямой х – 2 у – 7 = 0. Найти площадь этого квадрата.
2. Две стороны квадрата лежат на прямых 5 х – 12 у – 65 = 0 и 5 х – 12 у + 26 = 0. Найти площадь квадрата.
3. Найти уравнение прямой, проходящей через точку А (1, 2) так, чтобы расстояние от этой прямой до точек М 1 (2, 3) и М 2 (4, -5) были бы равны.
Пример 4. Написать уравнение прямой l 2, проходящей через точку А (0, 2) под углом p /4 к прямой l 1: х – 2 у + 3 = 0.
Смешанные задачи на прямую Задания для самостоятельного решения 1. Найти площадь треугольника, образованного прямыми 2 х + у + 4 = 0, х + 7 у – 11 = 0 и 3 х – 5 у – 7 = 0.
2. Составить уравнение прямой, проходящей через точку А (- 2, 1): а) параллельно оси Оу; б) образующей с осью Ох угол 3/ 4 p; в) перпендикулярно вектору а = { 4; 2 }; г) параллельно биссектрисе первого координатного угла; д) перпендикулярно прямой 6 х – у + 2 = 0; е) отсекающей на оси Оу отрезок длиной 5.
3. Дан четырехугольник ABCD с вершинами А (3, 5), B (6, 6), C (5, 3), D (1, 1). Найти: а) координаты точки пересечения диагоналей; б) угол между диагоналями.
4. Луч света, пройдя через точки А (4, 6) и B (5, 8), упал на прямую х – 2 у + 2 = 0 и отразился от нее. Составить уравнение прямой, по которой направлен отраженный луч.
5. Известны вершины треугольника А (-4, -2), B (0, 1), C (2, -1). Найти расстояние от начала координат до точки пересечения медианы, проведенной из вершины А, с высотой, проведенной из вершины В.
6. Найти координаты основания перпендикуляра, опущенного из точки А (-1, 2) на прямую 3 х – 5 у – 21 = 0.
7. Дан треугольник с вершинами в точках А (2, 5), B (5, -1), C (8, 3). Составить уравнение прямой, проходящей через точку пересечения медиан треугольника перпендикулярно к прямой х + у + 4 = 0.
8. Известны уравнения прямых, на которых лежат две стороны ромба: х + 2 у – 4 = 0, х + 2 у – 10 = 0 и уравнение одной из его диагоналей х – у + 2 = 0. Найти координаты вершин ромба.
9. Дан треугольник ABC с вершинами в точках А (2, 5), B (5, -1), C (8, 3). Найти координаты центра описанной около треугольника окружности.
10. Даны две вершины равносторонненго треугольника ABC: А (-6, 0), B (0, 0). Найти координаты третьей вершины С.
11. Даны вершины треугольника ABC: А (2, -2), B (3, 5), C (6, 1). Найти: а) длины сторон АС и ВС; б) уравнения прямых, на которых лежат стороны АС и ВС; в) уравнение прямой, на которой лежит высота, проведенная из точки В; г) длину этой высоты; д) уравнение прямой, на которой лежит медиана, проведенная из точки А; е) длину этой медианы; ж) уравнение прямой, на которой лежит биссектриса угла С; з) центр тяжести треугольника; и) площадь треугольника; к) угол С.
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.181 (0.009 с.) |






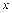
 фициентом y = k 1 x + b 1и y = k 2 x + b 2,
фициентом y = k 1 x + b 1и y = k 2 x + b 2,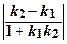 .
. (или k 1 k 2 = – 1).
(или k 1 k 2 = – 1). = { A 1; B 1} и
= { A 1; B 1} и = { A 2; B 2}:
= { A 2; B 2}: .
. (или A 1 B 2 – А 2 B 1 = 0).
(или A 1 B 2 – А 2 B 1 = 0). или
или 
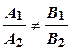 , то имеется единственная точка пересечения прямых;
, то имеется единственная точка пересечения прямых; , прямые не имеют общей точки, т.е. параллельны;
, прямые не имеют общей точки, т.е. параллельны;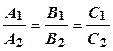 , прямые совпадают.
, прямые совпадают.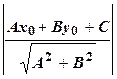 .
.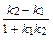 =
=  =
=  =
= 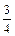 , φ = arctg
, φ = arctg 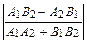 =
=  =
=  = 1, φ =
= 1, φ =  .
. х –
х –  . Здесь k 2 = –
. Здесь k 2 = – 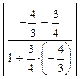 =
=  = ∞, φ =
= ∞, φ =  .
.