Взаимное пересечение многогранников

 

Линия пересечения двух многогранников может быть построена двумя способами.

Первый способ состоит в определении точек пересечения ребер первого многогранника с гранями второго многогранника и ребер второго с гранями первого, т.е. задача сводится к многократному решению задачи по определению точки пересечения прямой с плоскостью.

Второй способ состоит в определении линий пересечения граней одного многогранника с гранями другого. Задача сводится к определению линии пересечения двух плоскостей. Преимущество отдается тому из способов, который в зависимости от условия задания дает наиболее простое и точное решение. Эти два способа построения линии пересечения двух многогранников часто комбинируют между собой.

Линия пересечения двух многогранников представляется в общем случае в виде пространственных замкнутых ломаных линий. В зависимости от вида многогранников и их взаимного расположения линией пересечения может быть одна, две и более ломаных линий (в частности могут быть и плоские ломаные линии). Отрезки ломаных линий являются отрезками прямых, по которым пересекаются грани двух многогранников. Вершины ломаной линии этой точки пересечения ребер одного многогранника с гранями другого, и ребер второго с гранями первого. Отрезки ломаной линии строятся как отрезки прямых, соединяющих только те пары вершин, которые принадлежат одной и той же грани первого многогранника, а также одной грани второго многогранника. Вершины ломаной линии соединяются при строгом соблюдении последовательности.

Задача: Построить линию пересечения прямой четырехугольной призмы с треугольной пирамидой (рис.5.9).

 

Рис. 5.9. Построение линии пересечения пирамиды и

призмы

 

Решение:

Призма своим основанием стоит на горизонтальной плоскости проекций Н. Горизонтальные проекции ее вертикальных ребер вырождаются в точки. Грани боковой поверхности призмы проецируются в отрезки прямых. Линия пересечения многогранников определяется по точкам пересечения ребер каждого из них с гранями другого многогранника. Так, ребро SA пирамиды пересекается с двумя вертикальными гранями призмы в точках 1 (1_V,1_H) и 2 (2_V,2_H).

Ребро SB пирамиды пересекает две вертикальные грани призмы в точках 3(3_V,3_H) и 4(4_V, 4_H) и ребро SC – в точках 5(5_V, 5_H) и 6(6_V, 6_H). Из четырех вертикальных ребер призмы только одно пересекает пирамиду. Находим точки его пересечения с гранями пирамиды. Через это ребро и вершину S пирамиды проводим вспомогательную горизонтально проецирующую плоскость Q. На рис.5.9 показан горизонтальный след этой плоскости Q_H. Плоскость Q пересекает пирамиду по двум прямым линиям SK и SF, которые пересекаются с ребром призмы в точках 7(7_V, 7_H) и 8(8_V, 8_H). Последовательность построения точек 7_V и 8_V на рис.5.9 показана с помощью стрелок.

Соединяя каждые пары точек, принадлежащих одной и той же грани, получаем две ломаные линии пересечения многогранников. Одна из них пространственная ломаная линия 137581, другая – треугольник 246 – плоская ломаная линия лежащая в грани призмы. Видимость линии определяем с помощью конкурирующих точек.

 

Развертки многогранников

Совмещение всех граней многогранника с одной плоскостью путем последовательного вращения их вокруг ребер называется разверткой многогранника.

Все грани многогранника на развертке изображаются в натуральной величине. Поэтому построение развертки сводится к построению натуральных величин граней многогранника. Их расположение и последовательность могут быть различны.

Чтобы получить развертку выпуклого многогранника нужно на его поверхности провести линию разреза, которая должна удовлетворять трем условиям:

1) проходить через все вершины выпуклого многогранника;

2) не должна быть замкнутой;

3) состоять из связанных между собой участков (линия разреза должна представлять собой одну линию).

Задача: Построить развертку прямой четырехугольной усеченной призмы, с основанием на плоскости Н, (рис. 5.10).

Решение.

1. Определяем линию разреза многогранника для построения развертки (САВD4312).

2. Устанавливаем, что нижнее основание (АВСD) призмы изображено в натуральную величину на горизонтальной плоскости проекций, а ребра призмы изображены в натуральную величину на фронтальной плоскости проекций.

3. Определяем натуральную величину верхнего основания (сечения) призмы методом вращения вокруг проецирующей оси проходящей через точку 1 перпендикулярно плоскости V: (1\_н, 2\_н, 3\_н, 4\_н - натуральная величина сечения).

Рис. 5.10 – Построение развертки прямой четырехугольной

усеченной призмы

4. Строим развертку призмы. На горизонтальной линии отложим отрезки DВ = D_нВ_н; ВА = В_нА_н; АС = А_нС_н; СD = С_нD_н (ширина каждой из боковых граней).

На перпендикулярах к этим отрезкам откладываются величины ребер D4=D_v4_v; В2=В_v2_v; А1=А_v1_v; С3=С_vЗ_v.

Многоугольник D42134D представляет собой развертку боковой поверхности призмы. Нижнее основание призмы, равное горизонтальной проекции его (А_нВ_нD_нС_н) пристраивается, например, к стороне СD развертки боковой поверхности призмы. Натуральная величина основания (1_н2’_н3’_н4’_н) примыкает к развертке боковой поверхности стороной 24.

 

 

Глава 6. КРИВЫЕ ЛИНИИ

6.1. Основные определения и проекции кривых

Кривая в начертательной геометрии определяется как множество последовательных положений точки, непрерывно перемещающейся в пространстве с изменением направления движения. Если движение точки изменяется по определенному закону, то кривая называется закономерной. Если движение произвольное, то получается кривая общего вида.

Кривые линии могут быть плоскими и пространственными. У плоской кривой все точки инцидентны некоторой плоскости. Закономерные плоские кривые могут определяться своими уравнениями - алгебраическими (окружность, гипербола, эллипс, парабола и др.) или трансцендентными (спираль Архимеда, синусоида). Кривые общего вида могут задаваться только графически. Степень уравнения алгебраической кривой определяет ее порядок. Графически порядок кривой определяется количеством точек пересечения с прямой, причем точки берутся как действительные, так и мнимые. Порядок кривой сохраняется и у проекций кривой. Если спроецировать кривую b на плоскость Н по направлению S, то на ней получится проекция кривой b_H, обладающая всеми свойствами, которые сохраняются при параллельном проецировании (см. рис.6.1).

 

Рис. 6.1 – Проекция кривой Рис. 6.2 – Касательная к

B на плоскость Н кривой b

 

 

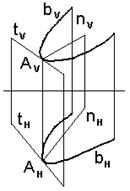
Касательной t к плоской кривой b в точке A называется предельное положение секущей t₁, когда точки A₁ и A₂, оставаясь на кривой b, стремятся к точке A (рис.6.2).

Нормалью n к кривой b в точке A называют прямую инцидентную плоскости P и перпендикулярную к касательной t в этой точке. К плоской кривой может быть проведена только одна нормаль. К пространственной кривой в данной точке можно провести бесчисленное множество перпендикуляров к касательной, которые определяют нормальную плоскость.

Касательная к кривой в заданной точке проецируется в касательные к ее проекциям (t_H; t_v). Проекции нормали (n_H; n_V) (рис.6.3) не перпендикулярны к проекциям (t_H; t_v) на чертеже, если плоскость, в которой находится кривая – плоскость общего положения (см. рис. 6.1)

Рис. 6.3 – Проекция кривой b на эпюре

Монжа

 

На кривой можно выделить обыкновенные, особые и экстремальные точки.

Обыкновенная точка А кривой характеризуется тем, что направление движения точки по кривой и направление касательной остаются неизменными (см. рис. 6.2).

Если же в данной точке меняется направление касательной или направление самой кривой, точка является экстремальной или особой.

Рассмотрим некоторые из особых точек.

1.Точка перегиба E, в которой касательная и нормаль меняют направление, а кривая пересекает касательную (рис. 6.4а).

2. Вершина кривой B – точка, в которой нормаль является осью симметрии для некоторого участка кривой (рис. 6.4б).

3.Точки возврата O и C (клюв), в которых ветви кривой имеют общую касательную (рис. 6.4 в, г).

4. Двойная точка (F, F₁), в которой кривая пересекает самое себя и меняется направление касательной (рис. 6.4 д, е).

 

Пространственные кривые

Кривую, точки которой не лежат в одной плоскости, называют пространственной или линией двоякой кривизны.

Пространственные кривые так же, как и плоские, могут быть закономерными или общего вида. К закономерным относятся винтовые линии (гелисы), которые широко применяются в технике, являясь определяющими поверхностей резьбы, червяков, пружин и т.п. Название винтовой линии определяется видом поверхности, по которой движется точка, образующая гелису.

Цилиндрическая винтовая линия.

Цилиндрическая винтовая линия представляет собой траекторию точки, равномерно движущейся по образующей цилиндра, которая, в свою очередь, равномерно вращается вокруг оси цилиндра.

 

Рис. 6.4. Особые точки на линии

 

Основными параметрами этой кривой являются: диаметр окружности цилиндра, шаг р винтовой линии, направление винтовой линии и угол подъема y. Шагом р называется расстояние, пройденное точкой по образующей цилиндра за один полный оборот по окружности. Шаг может быть постоянным и переменным. Если винтовая линия поднимается по видимой стороне цилиндра слева на право, то она правая. Угол подъема винтовой линии выражается формулой:

 

tg y= р/pd

 

где: р – шаг винтовой линии;

d – диаметр основания цилиндра.

Для построения проекций винтовой цилиндрической линии шаг (высота цилиндра) и окружность основания делятся на одинаковое число (n) равных частей. На рисунке 6.5 n=12.

При перемещении на 1/12 часть по окружности точка переместится на (1/12) р (шага) по образующей цилиндра. Таким образом, фронтальные проекции точек гелисы получаются при пересечении горизонтальных прямых деления шага с линиями проекционной связи, проведенными из соответствующих точек деления окружности (см. рис.6.5). Так как ось цилиндра является горизонтально-проецирующей прямой, то горизонтальная проекция гелисы совпадает с окружностью основания цилиндра. Фронтальная проекция цилиндрической винтовой линии - синусоида.

Рис. 6.5. Цилиндрическая винтовая линия и ее развертка

 

Разверткой гелисы является гипотенуза прямоугольного треугольника, один из катетов которого равен шагу р, а второй – длине окружности основания цилиндра pd. Из этого треугольника определяется и угол y.

Винтовая линия является линией кратчайших расстояний между двумя точками на поверхности цилиндра.

 

 

Глава 7. КРИВЫЕ ПОВЕРХНОСТИ

Общие сведения

Поверхность можно представить и как след, оставляемый линией при ее непрерывном движении в пространстве. Линию, которая перемещается в пространстве, называют образующей поверхности, а линии, которые определяют движение образующей – направляющими поверхности. Способ образования поверхности движением линии называется кинематическим, а поверхности, полученные этим способом – также кинематическими.

Кинематический способ позволяет задать поверхность на чертеже минимальным числом линий и точек.

Определитель поверхности должен включать условия, позволяющие задать данную поверхность на чертеже. Некоторые из параметров определителя могут быть заданы графически (вид и положение образующих или направляющих поверхности) или аналитически (величина радиуса сферы, угол наклона образующей конуса к его оси и т.п.), но кроме этих параметров необходимо задать еще способ (алгоритм) построения на чертеже точек и линий, принадлежащих поверхности.

Таким образом, каждый определитель поверхности включает в себя графоаналитическую и алгоритмическую характеристику поверхности. Одна и та же поверхность может быть образована по различным законам, т.е. иметь несколько различных определителей.

Определитель поверхности: F{l,i}[A₁]

Где {l,i} – графическая часть определителя;

[A₁] – алгоритм (закон) образования поверхности.

Образующая поверхности может быть прямой и кривой линиями, постоянной и переменной.

По виду образующей, поверхности делятся на линейчатые (прямо линейчатые) и не линейчатые (криво линейчатые).

Направляющих может быть несколько или одна. Любая линейчатая поверхность должна иметь три направляющие. У кривых поверхностей направляющими являются также кривые.

Поверхности разделяются на развертывающиеся и не развертывающиеся. Развертывающиеся поверхности могут быть совмещены с плоскостью без разрывов и складок. Их смежные образующие должны быть параллельными или пересекающимися прямыми. У не развертывающихся поверхностей смежные образующие должны быть скрещивающиеся прямые или кривые. Все не линейчатые поверхности – не развертывающиеся.

 

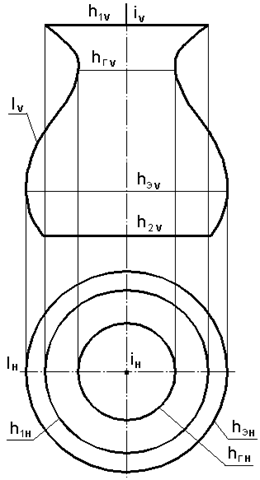
Поверхности вращения

Поверхностью вращения называется поверхность, получаемая вращением какой-либо линии или кривой, как плоской, так и пространственной вокруг некоторой оси.

Любая поверхность вращения может быть задана образующей l и осью вращения i. Определитель поверхности вращения: F{l,i}[A₁], где [A₁] –алгоритм образованияповерхности (вращения).

Поверхность вращения задают на чертеже проекциями образующей и осью вращения,. Каждая точка образующей l описывает окружность h с центром на оси i (рис.7.1).

Рис. 7.1. Поверхность вращения на эпюре Монжа

 

 

Эти окружности лежат в плоскостях, перпендикулярных оси вращения, и называются параллелями. Обычно ось вращения направлена перпендикулярно к какой-либо плоскости проекции, поэтому параллели проецируются на эту плоскость в натуральную величину. Наибольшая из параллелей называется экватором, а наименьшая горлом. Плоскость, проходящая через ось вращения, называется меридиональной плоскостью, а линия ее пересечения с поверхностью вращения – меридианом. Меридиан, параллельный фронтальной проекции называется главным меридианом. Главный меридиан определяет очерк поверхности вращения на фронтальной плоскости проекций, а на горизонтальной плоскости проекций очерк поверхности ограничивается экватором h_Э, горлом h_Г, верхней h₁ и нижней h₂ параллелями.

Поверхность вращения называется закрытой, если меридиан является замкнутой кривой, пересекающей ось в двух точках. Каждая из параллелей пересекает меридиан под прямым углом, т.е. параллели и меридианы образуют прямоугольный каркас поверхности.

Экватор h_Э является границей видимости поверхности вращения для горизонтальной плоскости проекций, а главный меридиан - для фронтальной плоскости проекций.

К линейчатым поверхностям вращения относятся: цилиндрическая, коническая и однополостный гиперболоид вращения.

Так как прямая безгранична, то линейчатые поверхности вращения ограничивают двумя параллельными плоскостями и получают тела вращения; цилиндр, однополостный гиперболоид, конус. У конуса вращения одна из ограничивающих плоскостей проходит через вершину.

Если главным меридианом поверхности является кривая второго порядка, то поверхность называется поверхностью вращения второго порядка. Эти поверхности имеют общий определитель F{l²,i}[A₁],

где: l² – кривая второго порядка; а i – ось вращения.

Наиболее распространены следующие поверхности второго порядка, которые образуются при вращении: цилиндр – кривой второго порядка, распавшейся на две параллельные прямые; конус – кривой второго порядка, распавшейся на две пересекающиеся прямые; сфера – окружности вокруг оси, совпадающей с ее диаметром; эллипсоид – эллипса вокруг одной из его осей; параболоид – параболы вокруг ее оси.

При вращении кривой второго порядка вокруг оси, не совпадающей с осью самой кривой, могут быть образованы поверхности вращения более высокого порядка. К таким поверхностям относится тор.

Тором называется поверхность, образованная при вращении окружности вокруг оси, инцидентной ее плоскости, но не проходящей через центр. В зависимости от величины r – радиуса образующей окружности и расстояния R от ее центра до оси вращения возможны три варианта поверхности тора.

Вариант 1: r<R –открытый тор или круговое кольцо (рис. 7.2).

Вариант 2: r=R – закрытый тор (образующая касается оси).

Вариант 3: r>R – закрытый тор (двуполостной).

Определитель тора может быть задан двумя параметрами r и R.

Ф{R, r}[А₁] или Ф{(0, r) i }[А₁], где: r – радиусобразующей окружности; 0 – центр этой окружности; i – ось вращения.

Если нужно построить точку на поверхности вращения, то строят одну из параллелей (h) и на ней задают точку (например, точка L на рис. 7.2).

Рис. 7.2. Поверхность тора и точка L на ее поверхности