Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о проекциях прямого углаСодержание книги
Поиск на нашем сайте
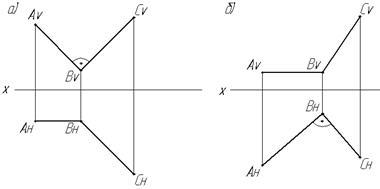
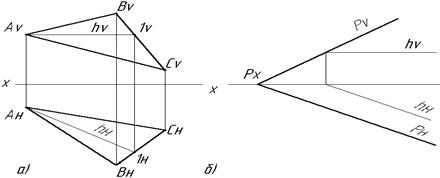
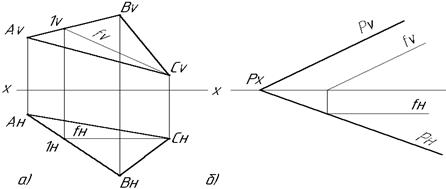
Для того, чтобы прямой угол проецировался ортогонально в виде прямого угла, необходимо и достаточно, чтобы по крайней мере, одна из его сторон была параллельна плоскости проекций, а вторая – не перпендикулярна к этой плоскости (Рис.2.11а, б).
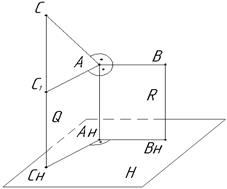
Рис. 2.11. Проекции прямого угла на эпюре: а) на фронтальной плоскости проекции; б) на горизонтальной плоскости проекции Доказательство: Пусть имеем в пространстве прямой угол ВАС. Проецируем его на плоскость Н ортогонально. Предположим, что сторона АВ данного угла параллельна плоскости Н. Тогда имеем: Ð ВАС = 90˚; АВ || Н; ААн ^ Н. Докажем, что Ð ВнАнСн = 90º (Рис.2.12). Ð АнАВ = 90°, т.к. фигура ААнВВн – прямоугольник. Следовательно, прямая АВ перпендикулярна к проецирующей плоскости Q как перпендикулярная к двум прямым этой плоскости (АВ ^ АС; АВ ^ ААн). Поэтому АВ ^ Q, но АнВн || АВ отсюда и АнВн ^ Q, а это означает, что Ð ВнАнСн = 90º.
Рис 2.12 Проекция прямого угла
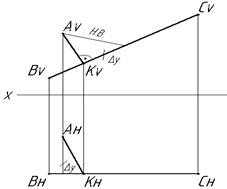
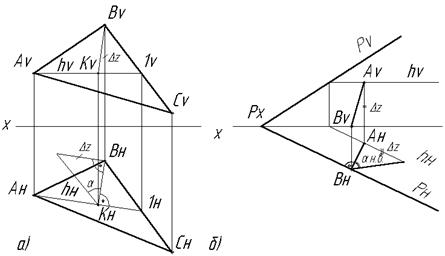
Задача: Определить расстояние от точки А до фронтали (Рис.2.13). Решение. Прямой угол между искомым перпендикуляром и фронталью ВС проецируется в натуральную величину на плоскость V. Натуральная величина перпендикуляра АК может быть найдена методом прямоугольного треугольника.
Рис. 2.13. Определение расстояния от точки А до фронтали ВС Ортогональные проекции плоскости
Плоскость представляет собой множество точек, которые при проецировании в общем случае покроют всю плоскость проекций, не давая на ней изображения. Поэтому плоскость в пространстве на проекциях определяют расположенные в ней элементы.
Рис. 2.14. Задание плоскости на эпюре
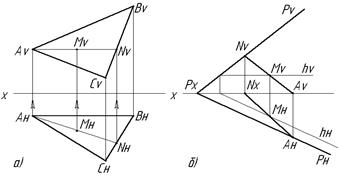
Такими элементами, определяющими плоскость, могут быть: три точки не лежащие на одной прямой (Рис.2.14а), прямой и не принадлежащей ей точки (Рис.2.14б), две параллельные прямые (Рис.2.14в), две пересекающиеся прямые (Рис.2.14г), плоская фигура (Рис.2.14д). Кроме этого плоскость может быть задана следами (Рис.2.15а, б).
Рис. 2.15. Задание плоскости следами: а) в диметрии; б) на эпюре Прямые, по которым данная плоскость пересекается с плоскостями проекций называются следами плоскости. Рн – горизонтальный след, Рv – фронтальный след и Рw – профильный след. Точки РX, РY, РZ называются точками схода следов.
Прямая и точка в плоскости
Задание плоскости на чертеже любым из перечисленных способов единственным образом определяет проекции всех точек и прямых, принадлежащих плоскости. Прямая CD, проходящая через две точки C и D, лежащие в плоскости, заданной прямыми АВ и CD, принадлежит этой плоскости (рис.2.16).
Рис. 2.16. Принадлежность прямой плоскости
Точка принадлежит плоскости, если через нее можно провести в этой плоскости прямую. Если точка М принадлежит плоскости АВС (Рис.2.17а, б), то по одной заданной проекции Мн можно определить другую проекцию Мv и притом единственную.
Рис. 2.17. Принадлежность точки плоскости: а) заданной прямоугольником; б) заданной следом Для этого через точку М (Мн) проведем какую-либо прямую АN (AнNн), принадлежащую данной плоскости; по линиям связи найдем вторую проекцию прямой (АvNv) и на ней соответствующую точку Мv. В качестве такой вспомогательной прямой часто берут линии уровня, лежащие в данной плоскости.
Особые линии плоскости К особым линиям плоскости относятся горизонталь плоскости, фронталь плоскости и линии наибольшего наклона к плоскости Н (линия ската). Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная плоскости Н (Рис.2.18а, б).
Рис 2.18 Горизонталь плоскости
Фронталь плоскости – прямая, лежащая в плоскости и параллельная плоскости V (Рис.2.19а, б).
Рис 2.19 Фронталь плоскости Линия ската S плоскости – это прямая, лежащая в плоскости и перпендикулярная к горизонтали плоскости (Рис.2.20а, б). Линия ската определяет угол наклона a плоскости к плоскости проекции Н.
Рис. 2.20 Линии ската плоскости: а)S =ВК в плоскости АВС; б) S=АВ в плоскости заданной следами РV и РH Плоскость на чертеже может быть задана линией ската и горизонталью (как двумя пересекающимися прямыми). Этот способ является рациональным, т.к. достаточно задать положение линии ската, а горизонталь строится перпендикулярно к ней.
Плоскости общего положения Плоскости не параллельные и не перпендикулярные ни одной из плоскостей проекций называются плоскостями общего положения. Такие плоскости изображены на рис. 2.14а, б, в, г, д.
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.171.192 (0.009 с.) |