Положения заданной прямыми линиями АВ и ВС

 

 

Для построения фронтальных проекций точек линии пересечения осуществляют обратную замену V₁® V, при этом сохраняется высота всех точек, т. е. Z=Z₁.

Для построения фронтальной проекции любой точки, например, точки 1, необходимо использовать условие |Z|=|Z₁|.

Полученные точки линии пересечения соединяют плавной кривой с учетом видимости. Видима та часть линии пересечения, которая расположена в передней половине поверхности цилиндра, т.е. линия 5_V,2_V,8_V,4_V,6_V, другая часть линии пересечения невидима.

 

Пересечение поверхности вращения с прямой линией

Прямая линия и поверхность вращения пересекаются в двух точках. Частным случаем пересечения может быть касание прямой и поверхности.

Для построения точек пересечения прямой линии с любой поверхностью необходимо:

· Через заданную прямую провести вспомогательную секущую плоскость Q.

· Построить линию b пересечения вспомогательной плоскости Q с заданной поверхностью Ф.

· В пересечении линии b и заданной прямой определить искомые точки (обе эти линии b и а лежат в одной плоскости Q, проведенной в качестве вспомогательной через прямую а).

· Определить видимость прямой.

Вспомогательную плоскость следует выбирать так, чтобы при пересечении поверхности этой плоскостью получались простые линии – окружности, прямые.

Чаще в качестве вспомогательных выбирают проецирующие плоскости, но иногда приходится применять и плоскости общего положения, пересекающие поверхность по простым линиям.

Задача: Построить точки пересечения поверхности вращения Ф с прямой АВ (рис.7.11).

Решение:

Задача решается по общей схеме:

Через прямую (АВ) проводится вспомогательная фронтально проецирующая плоскость Р^V.

Находится линия пересечения вспомогательной плоскости Р с поверхностью Ф – кривая второго порядка b.

Построение линии пересечения смотри в разделе 7.3.

Определяются горизонтальные проекции точек Е_H и F_H пересечения линии (АВ) и поверхности Ф.

По линиям связи находятся точки Е_V и F_V на проекции A_VB_V.

Видимость прямой АВ определяется по отношению к поверхности вращения Ф. Часть АВ, заключенная внутри поверхности вращения (между точками Е и F), не видна на обеих плоскостях проекций. На горизонтальной плоскости проекций точки Е и F видимы, т. к. они находятся над экватором поверхности вращения Ф. На фронтальной плоскости проекций точка Е видима, а F невидима, т.к. Е находится перед главным меридианом поверхности вращения Ф, а F за ним. По видимости точек Е и F определяется видимость АВ.

Задача: Построить точки пересечения цилиндра вращения Ф с прямой АВ (рис.7.12).

 

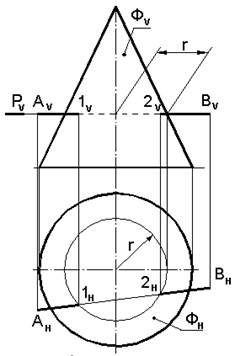
Рис. 7.11. Пересечение Рис. 7.12. Пересечение

Поверхности вращения цилиндра вращения Ф

Ф с прямой АВ с прямой АВ

Решение:

Решение упрощается, т.к. поверхность цилиндра Ф – горизонтально проецирующая (ось цилиндра перпендикулярна к плоскости Н) и горизонтальная проекция цилиндра – окружность Ф_Н. Следовательно, на горизонтальной плоскости проекций искомые точки определяют непосредственно по линиям связи.

Видимость прямой определяют по отношению к поверхности вращения Ф.

Задача: Построить точки пересечения конуса с прямой АВ (рис.7.13).

Решение:

Через прямую АВ проводится вспомогательная P_V фронтально-проецирующая плоскость перпендикулярная плоскости V.

Рис. 7.13. Пересечения конуса с прямой АВ

Находится линия пересечения вспомогательной плоскости с поверхностью Ф, которая представляет собой окружность радиусом r.

Определяются горизонтальные проекции точек пересечения 1_H и 2_H прямой АВ и поверхности Ф, как точки пересечения проекции А_HВ_H с окружность радиусом r.

По линиям связи находятся точки 1_V и 2_V на проекции A_VB_V.

Видимость прямой АВ определяется по отношению к поверхности вращения Ф. Часть прямой АВ, заключенная внутри поверхности вращения (между точками 1 и 2), не видна на обеих плоскостях проекций. На горизонтальной плоскости проекций точки 1 и 2 видимы, т. к. они находятся над основанием поверхности вращения Ф. На фронтальной плоскости проекций точки 1 и 2 также являютсявидимыми, так как они располагаются перед фронтальным меридианом.

Задача: Построить, точки пересечения конуса Ф с прямой АВ общего положения (рис.7.14).

Решение:

Для решения задачи в качестве вспомогательной рационально применить плоскость общего положения Р, проходящую через прямую АВ и вершину конуса S. Плоскость зададим двумя пересекающимися прямыми АВ и S1. Точка 1 берется произвольно на прямой АВ.

 

Рис.7.14. Пересечение конуса Рис.7.15. Пересечение сферы