А.А. Силич, Т.А. Миронова, Ф.В. Авдощенко

А.А. Силич, Т.А. Миронова, Ф.В. Авдощенко

 

КРАТКИЙ КУРС ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ

(технические специальности)

Учебное пособие

 

 

Курган 2002

 

УДК 514.18(07)

ББК 22.151.3я73

С-36

 

Силич А.А., Миронова Т.А., Авдощенко Ф.В. Краткий курс по начертательной геометрии для студентов заочной формы обучения (технические специальности):Учебное пособие. – Курган: Изд-во Курганского гос. университета, 2002. – 95с.

 

Учебное пособие предназначено, в первую очередь, в помощь студентам заочной формы обучения. В нем обобщен длительный опыт преподавания курса начертательной геометрии для студентов заочной формы обучения на кафедре начертательной геометрии и графики Курганского государственного университета. Данное учебное пособие вобрало в себя лучшие методические указания, которые в свое время были созданы опытнейшими преподавателями кафедры: Черемухиной Е.М, Шевалье Л.В, Денисовой Л.В., Колоколовой О.С. и др.

Материал, изложенный в пособии, соответствует обязательному минимуму федерального компонента по курсу начертательной геометрии для большинства технических специальностей и предназначен для начального знакомства с этим курсом. Более подробные и расширенные сведения студенты могут почерпнуть в литературе, список которой приведен в конце данного пособия.

Рис. 106. Библ.: 5 назв.

 

 

Печатается по решению редакционно-издательского совета Курганского государственного университета.

Научный редактор – доктор техн. наук, проф. Сызранцев В.Н.

Рецензенты: кафедра «Механики и черчения» Курганского военного института ФПС РФ. Зав. кафедрой доцент Гребенников В.Ф.

Доктор техн. наук, проф. Худорожков С.И.

 

 

ISB N 5-86328-358-0

Ó Курганский государственный университет, 2002

 

ВВЕДЕНИЕ

 

Начертательная геометрия – одна из учебных дисциплин, составляющих основу инженерного образования, она излагает методы, которые применяются при составлении и чтении чертежей.

В курсе начертательной геометрии рассматриваются следующие основные вопросы:

1) построение изображений пространственных форм на плоскости, т.е. составление чертежей;

2) решение геометрических задач в пространстве при помощи чертежей на плоскости, т.е. чтение чертежей.

Следовательно, в начертательной геометрии свойства предметов изучаются непосредственно по чертежу. Для того, чтобы чертеж был геометрически равноценным изображаемому предмету (оригиналу) он должен отвечать следующим требованиям:

1) чертеж должен быть наглядным;

2) чертеж должен быть обратимым, т.е. таким, чтобы по нему можно было точно воспроизвести форму и размеры изображаемого предмета;

3) чертеж должен быть достаточно простым для графического выполнения.

Для технических чертежей требование «обратимости» особенно важно. Чертеж является производственным документом, по которому выполняется то или иное изделие. Поэтому необходимо, чтобы по чертежу можно было точно установить форму и размеры будущего изделия. Никакое описание предмета не может заменить чертеж.

Для того, чтобы чертеж отвечал предъявляемым к нему требованиям, он должен быть построен по определенным геометрическим законам.

Геометрически закономерное изображение пространственного предмета на плоскости достигается при помощи метода проецирования (от латинского слова projicere – бросать вперед), который является основным методом в начертательной геометрии.

 

 

Глава 1. МЕТОД ПРОЕЦИРОВАНИЯ

 

Центральная проекция

 

Выберем в пространстве плоскость проекций, которую обозначим буквой Р. Выберем также точку S, не лежащую в плоскости Р, и назовем ее центром проекций (Рис.1.1).

Рис. 1.1. Центральная проекция точек

 

Плоскость Р и точка S составляют аппарат центрального проецирования. Проецирование проводится следующим образом: если дана произвольная точка А пространства, то для построения ее проекции на плоскость Р проводится прямая SA и находится точка пересечения А_р прямой SA с плоскостью Р. Точка А_р является центральной проекцией точки А на плоскость Р.

Прямая SA называется проецирующей.

Для построения проекций нескольких точек следует через взятые точки и центр проекций провести проецирующие прямые до пересечения их с плоскостью Р. Полученные точки и будут являться центральными проекциями соответствующих точек А, В, С.

При заданном центре и плоскости проекций данная точка имеет единственную проекцию, так как проецирующая прямая может пересечься с плоскостью проекций только в одной точке. Одна проекция точки не определяет ее положения в пространстве, т. к. на проецирующей прямой, например, SD_P может лежать множество точек, как-то точки D₁ и D₂ (Рис.1.1).

Параллельная проекция

 

Если центр проекций удалить в бесконечность, то проецирующие прямые станут параллельны между собой. Вместо центра проекций задается направление проецирования S (см. рис.1.2) и плоскость проекций Р. Проекции точек А, В и т.д. можно получить, если провести проецирующие прямые АА_р, ВВ_р и т.д., параллельно S.

Рис. 1.2. Параллельная проекция точек

А_р, В_р, С_р – проекции соответствующих точек.

В зависимости от направления проецирования параллельные проекции делятся на прямоугольные (S ^ P) и косоугольные (S не ^ Р).

 

Рис. 1.3. Проекции прямых линий Рис. 1.4. Проекции пересе-

Кающихся прямых

 

Рис. 1.5. Проекции параллельных Рис. 1.6. Проецирование

Прямых отрезков прямой

 

 

Рис. 1.7. Проекции отрезков параллельных прямых

 

Показатели искажения

 

Отношение длины проекции отрезка к длине самого отрезка называется показателем искажения К отрезка (Рис.1.6), величина которого определяется из следующего соотношения:

При косоугольном проецировании длина проекции может быть равна, больше или меньше длины самого отрезка. Показатель искажения может быть равен, больше или меньше единицы, т.е. 0 ≤ К ≤ ¥ (Рис.1.8).

Если отрезок BD параллелен плоскости проекций Р – он проецируется без искажения К=1. Если отрезок EF параллелен направлению проецирования S, он проецируется в точку К=0. Если величина угла между направлениями проецирования и плоскостью проекций близка к нулю, то длина проекции отрезка приближается к бесконечности К» ¥.

При прямоугольном проецировании длина проекции отрезка может быть равна или меньше длины самого отрезка. Показатель искажения может быть равен или меньше единицы 0 ≤ К ≤ 1 (Рис.1.9).

Из рассмотренных ранее рисунков (Рис.1.1 – Рис.1.9) видно, что при заданном направлении проецирования и плоскости проекций данная точка или система точек имеют единственную проекцию. Задав

 

Рис. 1.8. Коэффициент искажения Рис. 1.9. Коэффициент искаже-

Проецировании

 

плоскость проекций и направление проецирования можно получить изображение пространственной формы на плоскости проекций. Однако на одной проекции не выполняется требование обратимости, предъявляемое к чертежу, т.е. по одному изображению не возможно воспроизвести заданную форму в пространстве. Возникает необходимость изучения в курсе начертательной геометрии способов построения обратимых чертежей. Наиболее распространенным способом построения обратимых чертежей является прямоугольное проецирование на 2…3 взаимно перпендикулярные плоскости.

 

Аксонометрические проекции

 

Одним из видов обратимых чертежей является аксонометрический чертеж.

Аксонометрическая проекция – это параллельная проекция предмета, связанного с осями координат, на одну плоскость, которая называется плоскостью аксонометрических проекций. Тогда на изображениях осей могут быть нанесены линейные (или числовые) масштабы, пользуясь которыми можно определить размеры оригинала по его изображению (Рис.1.10).

А – аксонометрическое изображение точки А₁; XYZ – аксонометрическое изображение натуральной системы координат X₁; Y₁; Z₁; S – направление проецирования; Р – плоскость аксонометрических проекций.

 

Рис. 1.10. Модель образования аксонометрического

Изображения точки

 

Аксонометрические проекции относятся к наглядным видам изображений. Для получения наглядности положения предмета относительно плоскости аксонометрических проекций и направление проецирования выбирается так, чтобы на чертеже были получены изображения всех трех измерений аксонометрических осей (Рис.1.11).

 

Рис 1.11. Аксонометрическое изображение модели

В зависимости от направления проецирования аксонометрические проекции делятся на прямоугольные и косоугольные.

В зависимости от показателей искажения по осям аксонометрические проекции делятся на изометрию (показатели искажения по всем трем осям одинаковы), диметрию (показатели искажения равны лишь по двум осям) и триметрию (показатели искажения по всем трем осям различны).

 

Искажения

На рис.1.12. даны направления аксонометрических осей и показатели искажения для стандартных аксонометрических проекций.

 

Рис. 1.12. Направление аксонометрических осей и показатели искажения: а) изометрия прямоугольная; б) диметрия прямоугольная; в) диметрия косоугольная

XOZ – фронтальная плоскость V;

XOY – горизонтальная плоскость Н;

ZOY – профильная плоскость W.

Плоскости H, V, W в пространстве взаимно перпендикулярны.

Аксонометрическая проекция называется практической (или приведенной), если при ее построении используются практические показатели искажения. При применении практических показателей искажения по осям, в изометрии все изображение пропорционально увеличивается в 1,2 раза, а в диметрии в 1,06 раза.

 

Безосный эпюр

Изображения (проекции) точки, линии, плоской фигуры или пространственной формы на плоскостях проекций не изменятся, если плоскости перемещать по отношению к проецируемому объекту параллельно самим себе. При этом расстояния проецируемого объекта от плоскостей проекций изменяются, но это обстоятельство не имеет никакого значения для решения многих задач. Так, на технических чертежах оси проекций обычно не показывают. Поэтому на эпюре в ряде случаев можно не изображать осей проекций. Пример безосного чертежа точки приведен на рис.2.2в.

Рис. 2.2. Чертёж (эпюр) точки: а) на три плоскости проекции;

б) на две плоскости проекции; в) безосный

Прямые частного положения

К прямым частного положения относятся линии уровня – прямые, параллельные одной из плоскостей проекций, и проецирующие линии – прямые, перпендикулярные к одной из плоскостей проекций.

У куба с вырезом (Рис.2.4) линии, расположенные в гранях куба, параллельны плоскостям проекций будут линиями уровня.

Линия, параллельная горизонтальной плоскости проекций, называется горизонталью и на эпюре обозначается буквой h.

Линия, параллельная фронтальной плоскости проекций, называется фронталью и обозначается буквой f.

Линия, параллельная профильной плоскости проекций, называется профильной прямой и обозначается буквой р.

Ребра куба, стоящего на плоскости Н так, как это показано на рис. 2.4, параллельны двум плоскостям проекций и перпендикулярны третьей. Их направление совпадает с направлением проецирующих прямых при прямоугольном проецировании. В зависимости от перпендикулярности к той или иной плоскости проекций, прямые называются:

Рис 2.4 Прямые частного положения

 

· линия, перпендикулярная горизонтальной плоскости проекций Н, называется – горизонтально проецирующей прямой (прямая d);

· линия, перпендикулярная фронтальной плоскости проекций V, называется фронтально проецирующей прямой (прямая в);

· линия, перпендикулярная профильной плоскости проекций W, называется профильно проецирующей прямой (прямая с).

На рис.2.5 даны возможные положения прямых в системе плоскостей проекций в наглядном изображении и на эпюре. Фронтальная проекция горизонтали параллельна оси проекции Х, а на горизонтальной плоскости проекций она изображается в натуральную величину. На горизонтальной же проекции угол наклона горизонтали к фронтальной плоскости проекций изображается в натуральную величину. Аналогичны рассуждения относительно фронтали и профильной прямой.

Угол между прямой и плоскостью определяется углом между прямой и ее проекцией на эту плоскость. Угол наклона прямой к горизонтальной плоскости проекций обозначается - a, к фронтальной - b, к профильной - .

Рис 2.5 Проекция прямой частного положения

 

Прямая общего положения

Прямая, непараллельная ни одной из плоскостей проекций, называется прямой общего положения (Рис.2.6а, б).

Рис. 2.6 Прямая общего положения:

а)- в диметрии; б)- на эпюре

По проекциям отрезка прямой общего положения можно представить себе положение этого отрезка в пространстве. Однако, ни одна из проекций отрезка прямой общего положения не дает его натуральной величины и углов наклона к плоскостям проекций.

 

2.2.3 Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций

Натуральная величина отрезка прямой всегда может быть принята за гипотенузу прямоугольного треугольника, одним катетом которого является отрезок, равный и параллельный проекции, а другим – разность расстояний концов отрезка до плоскости проекций (Рис.2.7а, б).

Рис. 2.7. Определение натуральной величины отрезка и углов

наклона: а) в диметрии; б) на эпюре

В прямоугольном треугольнике АВВ - катет АВ = А_нВ_н; катет ВВ = Zв – Zа = ∆Z; гипотенуза АВ – натуральная величина отрезка, α – угол наклона прямой АВ к плоскости Н.

В прямоугольном треугольнике АВА - сторона А В = A_vB_v; сторона А А = Yа – Yв = ∆Y; сторона АВ – натуральная величина отрезка; β – угол наклона прямой к плоскости V.

 

Следы прямой линии

Точки пересечения прямой линии с плоскостями проекций называют следами прямой линии (Рис.2.8а, б).

Рис. 2.8. Следы прямой: а) в диметрии; б) на эпюре

 

Продолжим прямую АВ до пересечения с плоскостью Н. Получим точку М, которая является горизонтальным следом прямой. Продолжая прямую АВ до пересечения с плоскостью V получим точку N – фронтальный след прямой.

Чтобы на эпюре найти горизонтальный след, необходимо продолжить фронтальную проекцию A_vB_v до пересечения с осью Х; через точку пересечения М_v (фронтальную проекцию горизонтального следа) провести перпендикуляр к оси Х до пересечения с продолжением горизонтальной проекции прямой А_нВ_н. Точка пересечения М_н является горизонтальной проекцией горизонтального следа (она совпадает с самим следом М).

Для нахождения фронтального следа необходимо продолжить горизонтальную проекцию А_нВ_н до пересечения с осью Х; через точку N_н (горизонтальную проекцию фронтального следа) провести перпендикуляр до пересечения с продолжением фронтальной проекции A_vB_v. Точка N_v является фронтальной проекцией фронтального следа (она совпадает с точкой N – самим фронтальным следом прямой).

 

Конкурирующие точки

Точки, лежащие на одном перпендикуляре к плоскости проекций, называются конкурирующими относительно этой плоскости (Рис.2.10а, б).

По конкурирующим точкам определяется видимость геометрических образов на эпюре. Видимой на данной проекции всегда будет та из конкурирующих точек, которая лежит дальше от этой плоскости проекций, следовательно, ближе к зрителю. Точки А и В являются фронтально конкурирующими. На фронтальной плоскости проекции будет видима точка А, т.к. она дальше от плоскости V и ближе к наблюдателю. Точки А и С – горизонтально конкурирующие. На горизонтальной плоскости проекций будет видима также точка А, т.к. она отстоит от плоскости Н дальше, чем точка С.

Рис. 2.10. Конкурирующие точки: а) в диметрии; б) на эпюре

 

Проекции плоских углов

 

Две пересекающиеся прямые образуют плоский угол.

Если угол расположен в плоскости, параллельной плоскости проекций, то он проецируется на нее в натуральную величину.

В общем случае плоский угол, стороны которого не параллельны плоскости проекций, проецируется на эту плоскость с искажением.

 

Прямая и точка в плоскости

 

Задание плоскости на чертеже любым из перечисленных способов единственным образом определяет проекции всех точек и прямых, принадлежащих плоскости.

Прямая CD, проходящая через две точки C и D, лежащие в плоскости, заданной прямыми АВ и CD, принадлежит этой плоскости (рис.2.16).

Рис. 2.16. Принадлежность прямой плоскости

 

Точка принадлежит плоскости, если через нее можно провести в этой плоскости прямую. Если точка М принадлежит плоскости АВС (Рис.2.17а, б), то по одной заданной проекции М_н можно определить другую проекцию М_v и притом единственную.

Рис. 2.17. Принадлежность точки плоскости:

а) заданной прямоугольником; б) заданной следом

Для этого через точку М (М_н) проведем какую-либо прямую АN (A_нN_н), принадлежащую данной плоскости; по линиям связи найдем вторую проекцию прямой (А_vN_v) и на ней соответствующую точку М_v.

В качестве такой вспомогательной прямой часто берут линии уровня, лежащие в данной плоскости.

 

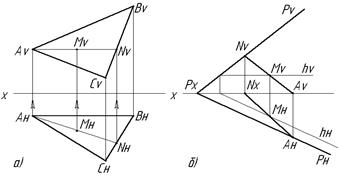
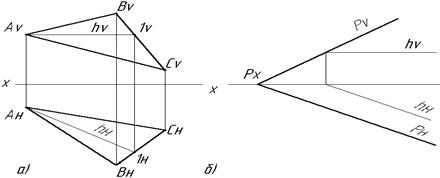
Особые линии плоскости

К особым линиям плоскости относятся горизонталь плоскости, фронталь плоскости и линии наибольшего наклона к плоскости Н (линия ската).

Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная плоскости Н (Рис.2.18а, б).

Рис 2.18 Горизонталь плоскости

 

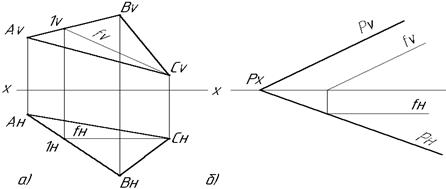
Фронталь плоскости – прямая, лежащая в плоскости и параллельная плоскости V (Рис.2.19а, б).

 

 

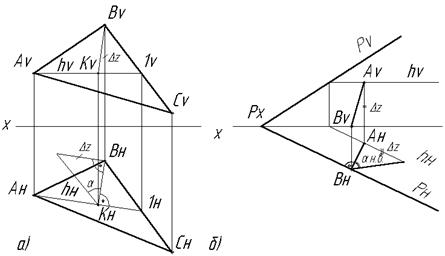
Рис 2.19 Фронталь плоскости

Линия ската S плоскости – это прямая, лежащая в плоскости и перпендикулярная к горизонтали плоскости (Рис.2.20а, б). Линия ската определяет угол наклона a плоскости к плоскости проекции Н.

Рис. 2.20 Линии ската плоскости:

а)S =ВК в плоскости АВС;

б) S=АВ в плоскости заданной следами Р_V и Р_H

Плоскость на чертеже может быть задана линией ската и горизонталью (как двумя пересекающимися прямыми). Этот способ является рациональным, т.к. достаточно задать положение линии ската, а горизонталь строится перпендикулярно к ней.

 

Плоскости общего положения

Плоскости не параллельные и не перпендикулярные ни одной из плоскостей проекций называются плоскостями общего положения. Такие плоскости изображены на рис. 2.14а, б, в, г, д.

 

Рис. 2.22 Проецирующие плоскости

Плоскости, параллельные плоскостям проекций (дважды проецирующие), называются плоскостями уровня (Рис.2.23а, б, в).

Рис. 2.23. Плоскости уровня

 

Все точки, лежащие в этих плоскостях, одинаково отстоят от соответствующей плоскости проекций. Любая плоская фигура, расположенная в плоскости уровня, проецируется на параллельную ей плоскость проекций без искажения, т.е. в натуральную величину.

 

Плоскостью общего положения

 

Возьмем горизонтально-проецирующую плоскость Р и плоскость общего положения АВС (рис.3.2а, б). На эпюре (рис.3.2б) плоскость Р проецируется в прямую Р_н. Линия пересечения двух плоскостей d – это линия, принадлежащая каждой из них, а следовательно, и горизонтально-проецирующей плоскости Р. Значит, горизонтальная проекция линии пересечения совпадает с горизонтальной проекцией плоскости d_н = Р_н. Построение фронтальной проекции линии пересечения сводится к построению точек 1_v и 2_v, принадлежащих фронтальным проекциям прямых АС и АВ. Фронтальная проекция d_v линии пересечения d проводится через точки 1_v и 2_v.

Рис. 3.2. Линия пересечения проецирующей плоскости с плоскостью общего положения: а)- в диметрии; б)- на эпюре

 

Рис 3.6. Построение линии пересечения двух плоскостей, не имеющих общих точек

Вводим горизонтальную плоскость – посредник Р (след P_v). Эта плоскость пересекает заданные плоскости по линиям уровня (горизонталям 1 - 2 и 3 - 4), в пересечении которых и лежит общая для всех трех плоскостей искомая точка I (проекции I_v и I_н). Для определения второй общей точки (II) проводится вспомогательная плоскость S.

 

Параллельные плоскости

 

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

У параллельных плоскостей соответственно параллельны линии уровня, линии ската и следы.

Задача: Через точку К провести плоскость, параллельную данной, задать ее линией ската и горизонталью (Рис.3.8).

Решение.

Провести в плоскости горизонталь и перпендикулярную ей линию ската. Через точку К провести плоскость, заданную двумя пересекающимися прямыми, одна из которых параллельна горизонтали, а вторая – линии ската.

Рис. 3.8. Параллельные плоскости

Рис. 3.11. Определение расстояния от точки до плоскости

 

 

Глава 4. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА

 

 

Решение позиционных и метрических задач значительно упрощается при преобразовании чертежа так, чтобы заданные геометрические объекты оказались в наиболее удобном – частном положении относительно плоскостей проекций. Это достигается либо способом замены плоскостей проекций, либо способом вращения.

 

Рис 4.4. Определение натуральной длины отрезка

а) и угла α; б) и угла β

Решение. На рис.4.4а выполнена замена фронтальной плоскости проекций V новой плоскостью V₁ проекция которой параллельна горизонтальной проекции отрезка АВ, поэтому плоскость V параллельна отрезку. Линии связи перпендикулярны новой оси Х₁. От новой оси на линиях связи отложены отрезки, равные расстояниям фронтальных проекций А_V и В_V точек до оси Х. В новой системе V₁/H отрезок АВ преобразовался во фронталь.

На рис.4.4б, показано решение этой же задачи, если отрезок АВ преобразовать в новой системе V/H₁ в горизонталь.

Задача: Преобразовать прямую общего положения в проецирующую (рис.4.5).

Решение. Для того, чтобы прямая общего положения в новой системе плоскостей проекций стала проецирующей, нужно последовательно решить рассмотренные первую и вторую задачи. Первой заменой преобразовать прямую в линию уровня фронталь. Второй заменой фронталь преобразовать в горизонтально-проецирующую прямую.

Рис 4.5. Преобразование чертежа

Задача: Определить расстояние между двумя параллельными прямыми k и m (рис.4.6).

Рис 4.6. Определение расстояния между прямыми

Решение. Так как m и k фронтали, то заменяем плоскость Н на Н₁, причем Н₁ берем перпендикулярно прямым m и k, чтобы они стали проецирующими.

 

4.1.2. Преобразование чертежа плоскости

Задача: Плоскость общего положения преобразовать в проецирующую (рис.4.7).

Решение. Заменим фронтальную плоскость проекций V на V₁, перпендикулярную к плоскости Н и к плоскости треугольника АВС. Чтобы плоскость V₁, была перпендикулярна плоскости треугольника, в его плоскости должна быть прямая, перпендикулярная к плоскости V₁. Такая прямая может быть горизонталь А1. Провести новую ось Х₁ перпендикулярно горизонтальной проекции горизонтали А_Н 1_Н. Треугольник АВС на плоскости V₁ спроецируется в прямую линию, т.е. станет фронтально-проецирующим. Угол между нею и осью Х₁ определит угол наклона к горизонтальной плоскости – угол a.

 

 

Рис 4.7. Преобразование плоскости общего положения

в проецирующую

 

Задача: Преобразовать проецирующую плоскость в плоскость уровня (рис.4.8).

Рис 4.8. Преобразование горизонтально проецирующей

Способ вращения

Сущность этого способа заключается в том, что плоскости проекций остаются неизменными, а изменяется положение геометрического объекта в пространстве вращением вокруг некоторой оси. В качестве оси вращения выбирают или проецирующую прямую, или линию уровня.

Рис 4.9. Преобразование плоскости общего положения

В плоскость уровня

Проекций

Допустим, что точка А, расположенная в пространстве вращается вокруг оси i, перпендикулярной к фронтальной плоскости проекций V (рис.4.10а).

Проекцией вращающейся точки А на фронтальной плоскости проекций является окружность, а на горизонтальной прямая линия перпендикулярная оси вращения или параллельно оси Х (рис.4.11). Если ось вращения i перпендикулярна к плоскости Н, то горизонтальная проекция точки описывает окружность, а ее фронтальная проекция перемещается параллельно оси Х (рис.4.11).

Задача: Повернуть отрезок АВ до положения прямой уровня (рис.4.12).

Решение. Повернем отрезок, например, до положения фронтали. Для этого за ось вращения примем горизонтально-проецирующую прямую i, проходящую через точку В. При вращении точка В остается неподвижной, остается повернуть вокруг оси i точку А до положения, чтобы заданный отрезок стал параллельным фронтальной плоскости

Рис 4.10. Вращение точки вокруг оси в диметрии

Рис 4.11. Вращение точки вокруг оси на юпюре

 

проекций. Горизонтальная проекция траектории точки А есть дуга окружности, а фронтальная проекция есть прямая параллельная оси Х. Для поворота отрезка АВ до положения горизонтали нужно за ось вращения принять фронтально-проецирующую прямую, проведенную через какую-нибудь точку отрезка АВ.

При решении этих задач можно определить натуральную величину углов наклона отрезка к плоскостям проекций a и b. На рис. 4.10 показан, например, угол a.

 

Рис.4.10 Вращение прямой вокруг проецирующей оси

 

 

4.2.2. Вращение без указания осей на чертеже –

Рис.4.11 Плоскопараллельное перемещение отрезка АВ

 

 

Задача: Определить натуральную величину треугольника АВС (Рис.4.12).

Решение.

1. Провести горизонталь А1 в треугольнике АВС.

2. Горизонталь А’_H1’_H построить перпендикулярно фронтальной плоскости на произвольном расстоянии от нее.

3. Методом засечек относительно горизонтали А’_Н1’_Н перенести горизонтальную проекцию треугольника в положение А’_НВ’_НС’ _Н (А_НВ_НС_Н = А’_НВ’_НС’_Н). По горизонтальной проекции треугольника построить фронтальную. Таким образом треугольник общего положения преобразовали во фронтально-проецирующую плоскость. Этим нашли угол наклона плоскости к горизонтальной плоскости проекций.

4. Перенести новую фронтальную проекцию треугольника А’_VВ’_VC’_V в положение А’’_VВ’’_VС’’_V параллельное горизонтальной плоскости проекций, достроить горизонтальную проекцию А’’_НВ’’_НС’’ _Н. Этим преобразовали фронтально-проецирующую плоскость в плоскость уровня, а именно в горизонтальную, следовательно горизонтальная проекция А’’_НВ’’_НС’’ _Н в натуральной величине.

Рис.4.12 Определение натуральной величины треугольника

Рис.4.13 Определение расстояния от точки А до линии СD способом вращения вокруг линии уровня

 

 

3.Отложить от центра О_Н на прямой, перпендикулярной к С_НD_Н, отрезок О_НА_О, равный натуральной величине радиуса R_A.

Задача: Определить натуральную величину треугольника АВС способом вращения вокруг горизонтали (Рис. 14).

Решение. Если за ось вращения построить горизонталь, принадлежащую плоскости треугольника АВС, то для поворота этой фигуры в положение, параллельное горизонтальной плоскости проекций, достаточно повернуть всего одну точку треугольника, не лежащую на оси вращения, а именно точку В. Остальные точки строятся из условия принадлежности их плоскости фигуры. Горизонталь А1 проведена через вершину А треугольника до пересечения с продолжением стороны ВС в точке 1. В треугольнике АВ1 вершины А и 1 лежат на оси вращения и не изменят своего положения при вращении вокруг горизонтали. Вращая точку В способом, рассмотренным на рис.4.13б, определяют положение ее новой проекции В¹. Соединив ее с точками А и 1, получим треугольник АВ’1, повернутый в положение, параллельное плоскости Н. Положение проекции точки С’, вершины С находят, проведя через точку С прямую перпендикулярную к оси вращения А1 до пересечения со стороной В1, поскольку все точки треугольника при его повороте перемещаются в параллельных плоскостях. Проекция А_НВ’_НС’_Н треугольника АВС определяет его натуральную величину, т.к. А_VВ’_VС’_V параллельна Н.

Глава 5. МНОГОГРАННИКИ

 

Общие положения

Многогранником называют геометрическое тело, ограниченное плоскими многоугольниками. Эти многоугольники называют гранями общие стороны смежных многоугольников – ребрами, вершины многогранных углов, образованных его гранями, сходящимися в одной точке - вершинами многогранника.

Совокупность вершин и соединяющих их ребер называют сеткой многогранника.

Рассмотрим только выпуклые многогранники, то есть такие, все грани которых лежат по одну сторону от каждой его грани.

Из всех многогранников наибольший практический интерес представляют призмы, пирамиды и правильные многогранники.

Многогранник, две грани которого n–угольники, лежащие в параллельных плоскостях, а остальные грани параллелограммы, называется n–угольной призмой.

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой призмой.

Если боковые ребра призмы не перпендикулярны плоскостям оснований, то она называется наклонной призмой.

Многогранник, одна из граней которого произвольный многоугольник, а остальные грани треугольники имеющие общую вершину, называется пирамидой (рис.5.1б).

Если основание пирамиды пр