
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ортогональные проекции точкиСодержание книги
Поиск на нашем сайте
Прямоугольные проекции на две или три взаимно перпендикулярные плоскости принято называть ортогональными. Зададим три взаимно перпендикулярные плоскости проекций и точку А в пространстве (Рис.2.1).
Рис. 2.1. Ортогональные проекции точки V, H, W – плоскости проекций V – фронтальная плоскость проекций H – горизонтальная плоскость проекций W – профильная плоскость проекций Линии пересечения плоскостей проекций X, Y, Z – оси проекций. Для того, чтобы получить три проекции точки А, следует из нее опустить перпендикуляры на плоскости проекций. Точки пересечения перпендикуляров с плоскостью V – фронтальная проекция точки Av, с плоскостью Н – горизонтальная проекция точки Ан, с плоскостью W – профильная проекция точки Аw. Для перехода к плоскому чертежу, эпюру (от французского слова epure – чертеж, проект) нужно плоскость Н повернуть вниз вокруг оси Х до совмещения с плоскостью V, а плоскость W совместить с плоскостью V, поворачивая ее вокруг оси Z вправо (Рис.2.2а). Две ортогональные проекции на взаимно перпендикулярные плоскости лежат на прямых, перпендикулярных к соответствующей оси проекции и пересекают эту ось в одной и той же точке. Эти линии называются линиями связи. Расстояние от точки до плоскостей проекций называются координатами этой точки и могут быть измерены по осям. 1) Расстояние ААw (ХА) от профильной плоскости проекций является абсциссой точки А; 2) Расстояние ААv (YА) точки А от фронтальной плоскости проекций называется ординатой (на рис.2.1 размер оси Y уменьшен в два раза, т.к. во фронтальной диметрии показатель искажения равен 0,5); 3) Расстояние ААн (ZА) точки А от горизонтальной плоскости проекций называется аппликатой точки А. Точка может быть задана ее координатами X, Y, Z, например, А ( Чертеж, на котором точка или система точек изображаются при совмещенном положении плоскостей проекций называется эпюром или чертежом. Границы плоскостей проекций на эпюре обычно не показываются. Во многих случаях бывает достаточно двух плоскостей проекций, в этом случае проводится только одна ось проекции Х (Рис.2.2б).
Безосный эпюр Изображения (проекции) точки, линии, плоской фигуры или пространственной формы на плоскостях проекций не изменятся, если плоскости перемещать по отношению к проецируемому объекту параллельно самим себе. При этом расстояния проецируемого объекта от плоскостей проекций изменяются, но это обстоятельство не имеет никакого значения для решения многих задач. Так, на технических чертежах оси проекций обычно не показывают. Поэтому на эпюре в ряде случаев можно не изображать осей проекций. Пример безосного чертежа точки приведен на рис.2.2в.
Рис. 2.2. Чертёж (эпюр) точки: а) на три плоскости проекции; б) на две плоскости проекции; в) безосный
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.195.90 (0.006 с.) |


 ,
,  ,
, 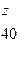 )
)



