Пересечение плоскости с прямой общего положения

 

Чтобы найти точку пересечения прямой общего положения АВ с плоскостью общего положения Q, нужно:

1) через прямую провести вспомогательную плоскость Р (посредник) частного положения;

2) построить линию пересечения (1 - 2) вспомогательной плоскости Р с заданной;

3) найти точку (I) пересечения заданной прямой с линией пересечения плоскостей (Рис.3.3).

Задача: Найти точку пересечения прямой FE с плоскостью, заданной треугольником ABC (Рис.3.4).

Рис. 3.3. Пересечение прямой линии с плоскостью

 

Рис. 3.4. Пресечение прямой линии с плоскостью на эпюре

 

Решение.

1. Проводим через прямую EF фронтально проецирующую плоскость Р (след Р_v);

2. Находим линию пересечения заданной и вспомогательной плоскостей (1-2);

3. В пересечении горизонтальных проекций прямых FE (F_нE_н) и 1 - 2 (1_н 2_н) находим горизонтальную проекцию точки пересечения прямой с плоскостью (I_н). Точка I_v строится по линии связи.

Видимость прямой и плоскости определяется по конкурирующим точкам (Рис.2.10а, б).

 

Взаимное пересечение плоскостей общего положения

 

Рассмотрим пример, в котором плоскости заданы треугольником и параллелограммом (Рис. 3.5). Требуется построить линию пересечения этих фигур. Для построения искомой линии достаточно найти две точки, в которых стороны одной фигуры пересекают плоскость другой фигуры. Поэтому возьмем одну из сторон параллелограмма, например, EF, и найдем точку пересечения ее с плоскостью треугольника. Для построения точки I, в которой прямая EF пересекает плоскость треугольника, проведем через EF горизонтально-проецирующую плоскость Р (след Р_н), находим проекции 1_н, 2_н и 1_v, 2_v линии пересечения проведенной вспомогательной плоскости Р с треугольником. В пересечении прямых 1_v 2_v и E_vF_v находим I_v и затем I_н, т.е. искомую точку. Таким же образом, посредством вспомогательной плоскости R, найдена точка II, в которой сторона параллелограмма DK пересекается с плоскостью треугольника. Остается соединить одноименные проекции найденных точек I и II.

Рис. 3.5. Взаимное пересечение плоскостей

Видимость плоских фигур определяется с помощью конкурирующих точек.

При помощи плоскостей – посредников можно найти общие точки, принадлежащие двум пересекающимся плоскостям, не имеющих общих точек на чертеже (Рис.3.6).

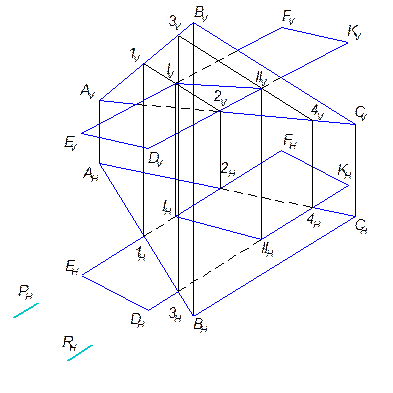
Рис 3.6. Построение линии пересечения двух плоскостей, не имеющих общих точек

Вводим горизонтальную плоскость – посредник Р (след P_v). Эта плоскость пересекает заданные плоскости по линиям уровня (горизонталям 1 - 2 и 3 - 4), в пересечении которых и лежит общая для всех трех плоскостей искомая точка I (проекции I_v и I_н). Для определения второй общей точки (II) проводится вспомогательная плоскость S.