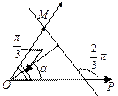Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные виды уравнения прямойСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Каждая прямая на плоскости Оху определяется линейным уравнением первой степени с двумя неизвестными. Обратно, каждое линейное уравнение первого порядка с двумя неизвестными определяет некоторую прямую на плоскости.
который прямая образует с положительным направлением оси Ох, k = tg α), b – ордината точки пересечения прямой с осью Оу.
Частные случая уравнения:
Ах + Ву = 0 (С = 0) – прямая проходит через начало координат; Ах + С = 0 (В = 0) – прямая параллельна оси Оу; Ву + С = 0 (А = 0) – прямая параллельна оси Ох;
а и b – длины отрезков (с учетом знаков), отсекаемых прямой на осях Ох и Оу соответственно.
y – y 0 = k (x – x 0)
k = tg α (α – угол, образуемый прямой с осью Ох); (x 0; у 0) – координаты данной точки.
5. Уравнение y – y 0 = k (x – x 0) называют также уравнением пучка прямых с центром в точке (x 0; у 0). Уравнение пучка прямых, проходящих через точку пересечения двух прямых А 1 х + В 1 у + С 1 = 0 и А 2 х + В 2 у + С 2 = 0 имеет вид:
А 1 х + В 1 у + С 1 + λ (А 2 х + В 2 у + С 2) = 0,
где λ – числовой множитель.
М 1(x 1; у 1) и М 2(x 2; у 2):
Если x 1= x 2, то уравнение будет иметь вид: x = x 1; если у 1= у 2, то у = у 1.
x cos α + y sin α – p = 0,
где р – длина перпендикуляра, опущенного из начала координат на прямую, α – угол, который этот перпендикуляр образует с положительным направлением оси Ох.
1. Для построения прямой достаточно знать координаты двух ее произвольных точек Полагаем, например, в уравнениии прямой х = 0, получим у = - 4Þ имеем одну точку А (0, - 4). Полагая х = 1, получим у = - 2Þ вторая точка В (1, - 2). Построим точки А и В и проведем через них прямую (рис.).
2. Задачу можно решить с помощью уравнения прямой в отрезках. Приведем уравнение к виду (3). Для этого перенесем свободный член (-4) в правую часть уравнения и разделим обе его части на 4. Получаем 2 х – у = 4, координат отложим 2 единицы вправо; на оси Оу отложим 4 единицы вниз. Получаем две точки на осях, через которую проводим прямую (рис.).
Задания для самостоятельного решения 1. Записать уравнение прямой у = 2 х – 3 в отрезках и построить ее.
2. Определить, при каком значении a прямая (a 2 – a) х + (2 + a) у – 3 a + 1 = 0
а) параллельна оси Ох; б) проходит через начало координат.
3. Найти k из условия, что прямая у = k х + 2 удалена от начала координат на расстоянии
4. Написать уравнение прямой, проходящей через точку А (-2, 2/5) и образующей с осью О х угол, равный arctg3.
Пример 2. Уравнение прямой 4 х – 3 у + 12 = 0 представить в различных видах (с угловым коэффициентом, в отрезнах, в виде нормального уравнения).
Для получения ур-ния прямой с угловым коэффициентом разрешим заданное уравнение относительно у. Получим: у = 4/3 х + 4, здесь k = 4/3, b = 4.
Для получения ур-ния прямой в отрезках перенесем свободный член С = 12 вправо и разделим обе части ур-ния на -12: Þ х /-3 + у /4 = 1 (а = –3, b = 4).
Задания для самостоятельного решения 1.
Задания для самостоятельного решения 1. Прямая проходит через точки А (2, 3) и В (-2, -1), пересекает ось Оу в точке С. Найти координаты точки С.
2. Какую абсциссу имеет точка М, лежащая на прямой, проходящей через точки А (-2, -2) и В (-1, 6), и имеющая ординату, равную 22?
Пример 4. Из пучка прямых, определяемых уравнением у + 3 = k (x – 2), выделить ту, которая проходит через точку А (-2, 5).
Подставим координаты точки А в уравнение прямой: 5 + 3 = k (– 2– 2), получим 8 = – 4 k Þ k = – 2. Следовательно, искомое уравнение прямой есть у + 3 = – 2 (x – 2) или 2 х + у –1 = 0.
Задание для самостоятельного решения Найти прямую, принадлежащую пучку –4 х + 2 у + 1 + l (х – 3 у + 2) = 0 и проходящую через точку А (1, 0). Написать ее уравнение.
1. Найти уравнение прямой: а) образующей с осью Ох угол p /3 и пересекающей ось Оу в точке (0, - 6); б) параллельной оси Ох и отсекающей на оси Оу отрезок, равный 2; с) отсекающей на осях координат, отрезки, равные 3 и 4.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 3806; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.189.63 (0.007 с.) |




 Уравнение прямой с угловым коэффициентом:
Уравнение прямой с угловым коэффициентом: 
 y = kx + b.
y = kx + b.

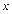
 Здесь: k – угловой коэффициент прямой (тангенс угла α,
Здесь: k – угловой коэффициент прямой (тангенс угла α,

 Общее уравнение прямой:
Общее уравнение прямой: 
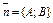 Ах + Ву + С = 0.
Ах + Ву + С = 0.
 Вектор
Вектор  = { A; B } – нормальный вектор прямой (
= { A; B } – нормальный вектор прямой ( перпендикулярен прямой).
перпендикулярен прямой).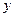
 Ах = 0 (В = С = 0) – прямая совпадает с осью Оу;
Ах = 0 (В = С = 0) – прямая совпадает с осью Оу;
 Ву = 0 (А = С = 0) – прямая совпадает с осью Ох.
Ву = 0 (А = С = 0) – прямая совпадает с осью Ох.




 Уравнение прямой в отрезках:
Уравнение прямой в отрезках:  = 1.
= 1. 


 Общее уравнение прямой можно преобразовать в нормальное уравнение путем умножения на нормирующий множитель
Общее уравнение прямой можно преобразовать в нормальное уравнение путем умножения на нормирующий множитель  ; знак берется противоположным знаку свободного члена С (в общем уравнении прямой).
; знак берется противоположным знаку свободного члена С (в общем уравнении прямой).
 Уравнение прямой в полярных координатах:
Уравнение прямой в полярных координатах:




 r cos (φ – α) = p.
r cos (φ – α) = p.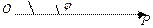


























 –
–  = 1, т.е.
= 1, т.е.  +
+  = 1 – уравнение прямой в отрезках. На оси Ох от начала
= 1 – уравнение прямой в отрезках. На оси Ох от начала .
.
 Записать данное уравнение с угловым коэффициентом, в отрезках и нормальном виде и определить, на каком расстоянии от начала координат оно находится: а) 2 х – 3 у + 6 = 0, б) х + 2,5 = 0, в) у = х – 1, г) х + 5 у = 0.
Записать данное уравнение с угловым коэффициентом, в отрезках и нормальном виде и определить, на каком расстоянии от начала координат оно находится: а) 2 х – 3 у + 6 = 0, б) х + 2,5 = 0, в) у = х – 1, г) х + 5 у = 0.






 а) А (0, 2), В (-3, 7); б) А (2, 1), В (4, 1).
а) А (0, 2), В (-3, 7); б) А (2, 1), В (4, 1).