
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условие принадлежности прямой плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. Прямая принадлежит плоскости, если две точки этой прямой принадлежат этой плоскости. 2. Прямая принадлежит плоскости, если она имеет с плоскостью одну общую точку и параллельна любой другой прямой, лежащей в этой плоскости.
2.2. Классификация плоскостей. Положение плоскости относительно плоскостей проекции.
1. Плоскость общего положения – непараллельна и неперпендикулярна ни одной из плоскостей проекции.
2. Плоскость уровня – плоскость параллельная какой-либо плоскости проекции; А) горизонтальная плоскость уровня - ║П1;
Вырожденная проекция обладает собирательными свойствами.
Б) фронтальная плоскость уровня - ║П2;
В) профильная плоскость уровня - ║П3.
3. Плоскости проецирующие – перпендикулярны какой-либо плоскости проекции, но непараллельны другим плоскостям проекций;
В) профильно-проецирующая – перпендикулярна П3, но непараллельна П1 и П2. 2.3. Взаимное расположение плоскостей Плоскости могут быть относительно друг друга: 1) Параллельные; Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
α║β a1║c1 b1║d1
2) Пересекающиеся; 3) Перпендикулярные; Плоскости перпендикулярны, если прямая одной плоскости перпендикулярна каждой из двух пересекающихся прямых другой плоскости. Плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой.
2.4. Взаимное положение прямой и плоскости. 1) Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости. 2) Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. 3) Прямая может пересекать плоскость.
2.5. Главные линии плоскости.
1. Горизонталь – прямая, лежащая в заданной плоскости и параллельная П1.
h0 – нулевая горизонталь
h0║h h20║h2
Все горизонтали плоскости параллельны между собой и параллельны нулевой горизонтали (т.е. горизонтальному следу).
2. Фронталь – прямая, лежащая в заданной плоскости и параллельная П2.
f0 – нулевая фронталь
f0║f f10║f1
Все фронтали плоскости параллельны между собой и параллельны нулевой фронтали (т.е. фронтальному следу).
3. Линия ската -линия наибольшего наклона заданной плоскости к плоскости проекции П1. Линия наибольшего наклона определяет угол наклона заданной плоскости к плоскости проекции П2 (расположена перпендикулярно всем фронталям). Линия ската определяет угол наклона заданной плоскости к плоскости проекции П1 (расположена перпендикулярно всем горизонталям).
Задача. Определить угол наклона плоскости α к плоскости проекции П1.
MN – линия ската M2N2 – фронтальная проекция линии ската M1N1 – горизонтальная проекция линии ската φ – угол наклона
План решения:
1. Строим линию ската (M1N1 ┴ α П1); 2. Для нахождения угла наклона необходимо определить угол наклона прямой MN к П1; Для этого построим прямоугольный треугольник, который определит не только Н.В. MN, но и угол наклона его к плоскости проекции П1. 2.6. Линия наибольшего наклона к П2.
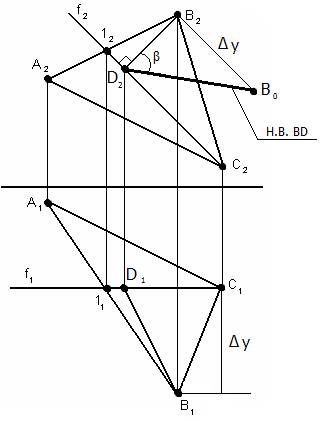
BD ┴ f
B2D2 ┴ f2
Для определения угла наклона плоскости АВС к плоскости проекций П2 необходимо определить Н.В. отрезка BD. Построения производим на той плоскости проекций, к которой необходимо определить угол наклона.
Лекция 3 Метрические и позиционные задачи. 3.1. Построение линии пересечения плоскостей. Задача I-го типа. Оба геометрических образа частного положения.
Решение: Проекции результата есть на чертеже и лежат на вырожденных проекциях проецирующих образов (построение не требуется).
Пример: Построить линию пересечения плоскости α с плоскостью β.
α – горизонтально-проецирующая плоскость
β – горизонтальная плоскость уровня
α Ո β = а
Один геометрический образ (ГО) частного положения, имеет вырожденную проекцию, а второй ГО общего положения (нет вырожденных проекций).
Решение: Одна проекция результата есть на чертеже и находиться на вырожденной проекции проецирующего образа (на П1 или П2), а другая определяется из условия принадлежности ко второму не проецирующему образу.
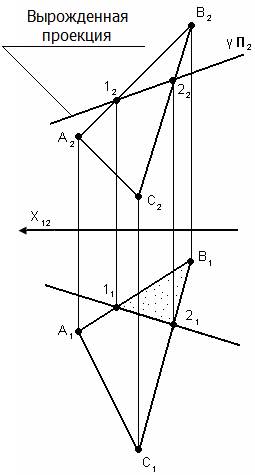
Пример: (АВС) – плоскость общего положения, γ – фронтально-проецирующая плоскость. ∆ АВС Ո γ = 12 1222 принадлежит γ П2
Задача III-го типа. Оба ГО общего положения.
Решение: При помощи посредников. В качестве посредников выбираются ГО частного положения и решение задачи сводится к решению задачи II-го типа. Пример: α – горизонтальная плоскость уровня, плоскость-посредник β – плоскость-посредник
3.2. Построение точки пересечения прямой с плоскостью.
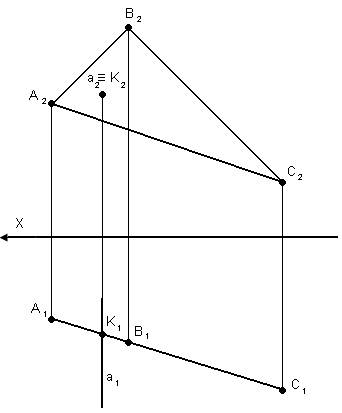
Оба геометрических образа частного положения. Прямая а – фронтально-проецирующая
(ABC) – горизонтально-проецирующая
Проекция результата лежит на вырожденных проекциях проецирующих образов.
K1 – на вырожденной проекции треугольника АВС.
К2 – на вырожденной проекции прямой а. АВС Ո а = К
Плоскость задана следами. Один ГО общего положения, второй частного положения.
α – плоскость общего положения.
Прямая а – горизонтально-проецирующая.
Горизонтальная проекция результата точка К1 лежит на вырожденной проекции прямой а, фронтальная проекция точки К2 определяется из условия принадлежности ко второму не проецирующему образу плоскости α.
α Ո а = К
Задача III-го типа. Оба ГО общего положения. Решаем при помощи посредника (плоскости частного положения). 1. Вводим плоскость-посредник β (β – частного положения и проходит через прямую а); 2. Определяем линию пересечения плоскости (АВС) – общего положения и плоскости β – частного положения. Решаем задачу II-го типа; 3. Выделяем искомую точку К как точку пересечения заданной прямой и линии пересечения плоскостей [1 - 2];
На эпюре:
2. (АВС) ∩ β = [1 - 2] Решаем задачу II-го типа;
3. а ∩ [1 - 2] = К.
Лекция 4 Взаимно-параллельные и взаимно-перпендикулярные прямые и плоскости. 4.1. Построение прямой параллельной плоскости. Для того чтобы провести через точку А прямую параллельную плоскости α необходимо: 1) в плоскости α выбрать или построить произвольную прямую; 2) через точку А провести новую прямую параллельную выбранной прямой.
a║ α a1║M1N1
Для того чтобы проверить, параллельна ли прямая плоскости необходимо попытаться в заданной плоскости построить прямую параллельную заданной. Если это удастся, то прямая и плоскость параллельны.
4.2. Построение параллельных плоскостей. Для того чтобы через точку А провести плоскость параллельную заданной необходимо в заданной плоскости провести две произвольные пересекающиеся прямые и через точку А провести новые прямые, соответственно параллельные выделенным (удобнее всего использовать прямые частного положения – горизонтали и фронтали).
Для того чтобы проверить параллельны ли две плоскости необходимо попытаться построить в этих плоскостях пересекающиеся прямые, которые были бы попарно параллельны.
α ║β h2║h2I h1║h1I
4.3. Построение прямой перпендикулярной плоскости.
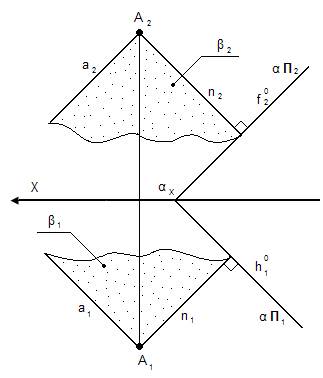
4.4. Построение взаимно-перпендикулярных плоскостей. Для того чтобы через точку А провести плоскость перпендикулярную заданной необходимо сначала построить прямую перпендикулярную заданной плоскости, а затем через эту прямую провести новую плоскость (решений бесконечное множество).
n – нормаль (перпендикуляр)
n ┴ α
α ┴ β n1 ┴ f10
Для того чтобы проверить перпендикулярны ли заданные плоскости необходимо в одной плоскости попытаться найти или построить перпендикуляр к другой.
n2 ┴ β П2
Лекция 5 Способы преобразования проекций.
Цель преобразований: ГО общего положения путем преобразования проекции привести к частному положению для упрощения решения метрических задач (нахождение площади, расстояния, углов).
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1897; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

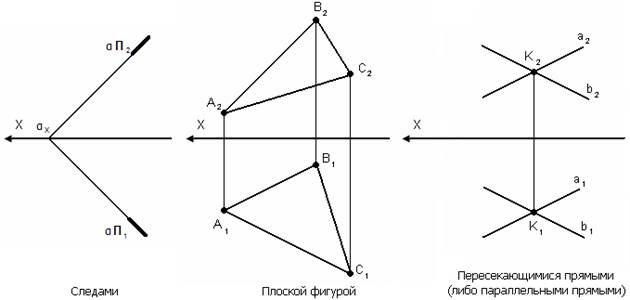 Может задаваться:
Может задаваться: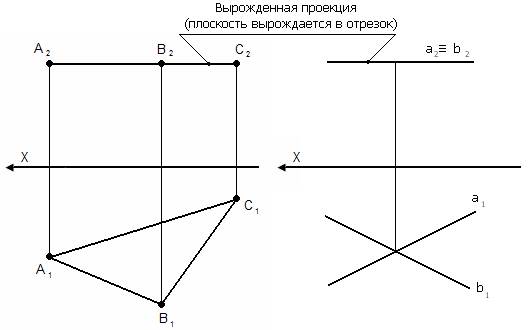
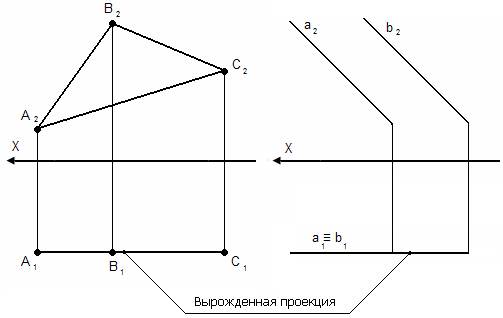
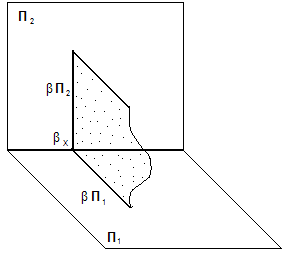
 А) горизонтально-проецирующая – перпендикулярна П1, но непараллельна П2 и П3;
А) горизонтально-проецирующая – перпендикулярна П1, но непараллельна П2 и П3;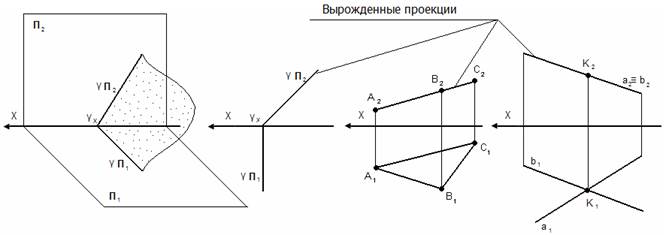 Б) фронтально-проецирующая – перпендикулярна П2, но непараллельна П1 и П3;
Б) фронтально-проецирующая – перпендикулярна П2, но непараллельна П1 и П3;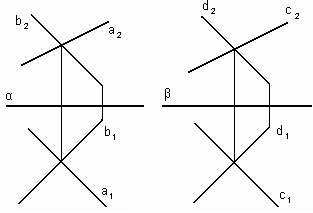
 a2║c2 b2║d2
a2║c2 b2║d2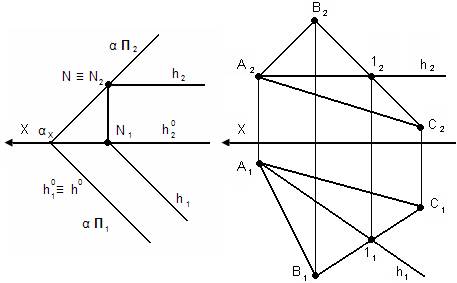
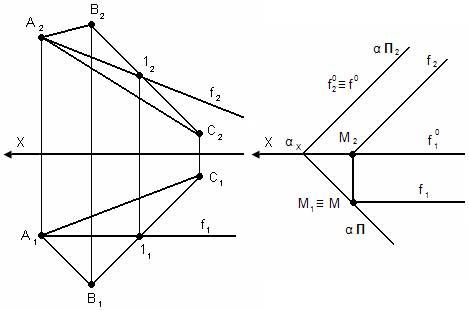
 f20║f2
f20║f2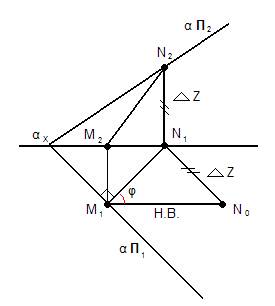

 Задача II-го типа.
Задача II-го типа.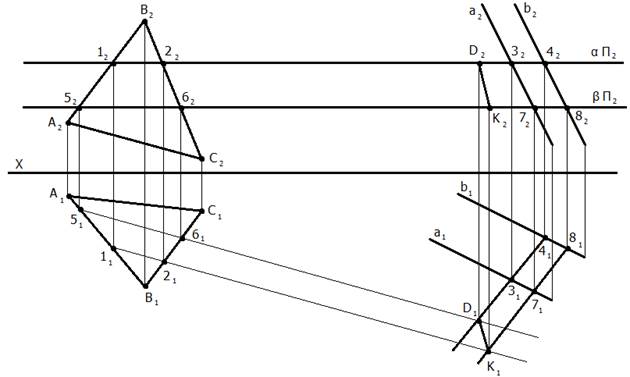
 Задача I-го типа.
Задача I-го типа.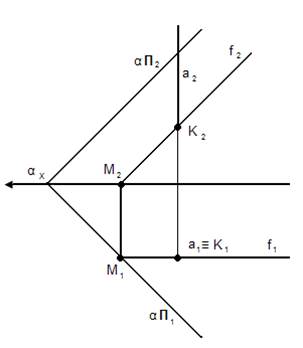 Задача II-го типа.
Задача II-го типа.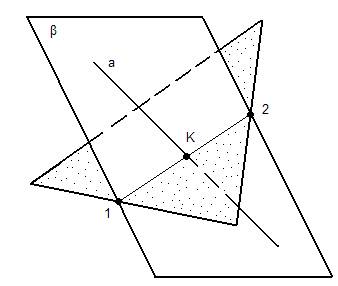 4. Определяем видимость элемента.
4. Определяем видимость элемента.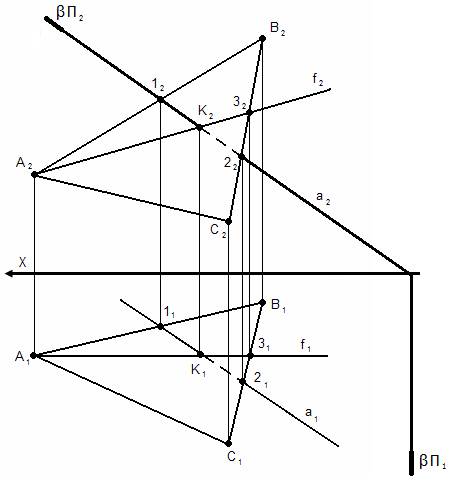 1. Прямая а принадлежит β, β перпендикулярна П2 (через прямую а провели фронтально-проецирующую плоскость β);
1. Прямая а принадлежит β, β перпендикулярна П2 (через прямую а провели фронтально-проецирующую плоскость β);
 a2║M2N2
a2║M2N2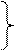 f2║f 2I f1║f 1I
f2║f 2I f1║f 1I
 Для того чтобы через точку А провести прямую перпендикулярную плоскости необходимо фронтальную проекцию прямой направить перпендикулярно фронтальной проекции фронтали плоскости, а горизонтальную проекцию прямой направить перпендикулярно горизонтальной проекции горизонтали плоскости.
Для того чтобы через точку А провести прямую перпендикулярную плоскости необходимо фронтальную проекцию прямой направить перпендикулярно фронтальной проекции фронтали плоскости, а горизонтальную проекцию прямой направить перпендикулярно горизонтальной проекции горизонтали плоскости.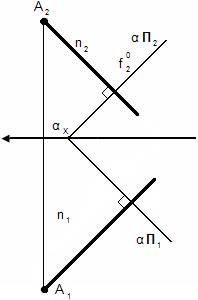
 n2 ┴ f20
n2 ┴ f20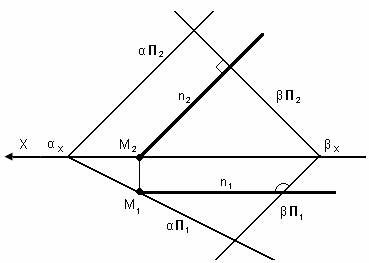
 n1 ┴ β П1
n1 ┴ β П1
 n1 ┴ β β ┴ α
n1 ┴ β β ┴ α


