
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное уравнение плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Положение плоскости Пусть
Общее уравнение плоскости
где знак берется противоположным знаку свободного члена
БИЛЕТ №30. Нахождение расстояния от точки до плоскости.
БИЛЕТ №31. Нахождение расстояния между параллельными плоскостями.
Расстояние между двумя параллельными плоскостями
Координаты точек
БИЛЕТ №32. Нахождение угла между плоскостями.
Две пересекающиеся плоскости Обозначим угол между плоскостями через
Наклон плоскости однозначно определяется её вектором нормали, поэтому угол между плоскостями равен углу между нормальными векторами данных плоскостей. А угол между векторами рассчитывается с помощью обыденной формулы, рассмотренной на уроке Скалярное произведение векторов:
Распишем формулу в коэффициентах:
БИЛЕТ №33. Условие перпендикулярности плоскостей.
Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, Таким образом,
БИЛЕТ №34. Общее уравнение прямой в пространстве.
Общее уравнение прямой в пространстве выводится из условия задания прямой, как пересечения двух плоскостей:
БИЛЕТ №35. Каноническое уравнение прямой.
БИЛЕТ №36. Параметрическое уравнение прямой в пространстве.
или (скорее 2)
БИЛЕТ №37. Уравнение прямой на плоскости, проходящей через заданные две точки.
Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки:
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:
если х 1 ≠ х2 и х = х 1, если х 1 = х2. Дробь Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4). Решение. Применяя записанную выше формулу, получаем:
БИЛЕТ №38. Нахождение точки пересечения прямой и плоскости.
Пример. Найдите координаты точки пересечения прямой Решение. Подставим в уравнение плоскости выражения Находим координаты точки пересечения прямой и плоскости по параметрическим уравнениям при Ответ: (3, 0, -1).
Пример. Если прямая Решение. Составим систему из заданных уравнений Последнее уравнение системы после прямого хода метода Гаусса стало неверным равенством, следовательно, система уравнений не имеет решений. Отсюда заключаем, что прямая Ответ: прямая параллельна плоскости и они не имеют точки пересечения.
БИЛЕТ №39.
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.43.200 (0.008 с.) |

 вполне определяется заданием единичного вектора
вполне определяется заданием единичного вектора  , имеющего направление перпендикуляра
, имеющего направление перпендикуляра  , опущенного на плоскость из начала координат, и длиной p этого перпендикуляра
, опущенного на плоскость из начала координат, и длиной p этого перпендикуляра , а
, а  – углы, образованные единичным вектором
– углы, образованные единичным вектором  и
и 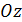 ;
;  Возьмем на плоскости произвольную точку
Возьмем на плоскости произвольную точку  и соединим ее с началом координат. Образуем вектор
и соединим ее с началом координат. Образуем вектор  . При любом положении точки Μ на плоскости
. При любом положении точки Μ на плоскости  на направление вектора
на направление вектора  :
:  , т.е.
, т.е.  или
или 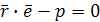 – нормальное уравнение плоскости в векторной форме. Записав его в координатах получим нормальное уравнение плоскости в координатной форме:
– нормальное уравнение плоскости в векторной форме. Записав его в координатах получим нормальное уравнение плоскости в координатной форме: .
. можно привести к нормальному уравнению так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части общего уравнения на нормирующий множитель
можно привести к нормальному уравнению так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части общего уравнения на нормирующий множитель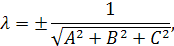
 общего уравнения плоскости.
общего уравнения плоскости.
 выражается формулой:
выражается формулой:

 нам неизвестны, да их и не нужно знать, поскольку перпендикуляр между плоскостями можно протянуть в любом месте.
нам неизвестны, да их и не нужно знать, поскольку перпендикуляр между плоскостями можно протянуть в любом месте.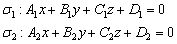 образуют четыре двухгранных угла и любой из этих углов можно считать углом между плоскостями. Иными словами, острый или тупой угол получится – не имеет значения.
образуют четыре двухгранных угла и любой из этих углов можно считать углом между плоскостями. Иными словами, острый или тупой угол получится – не имеет значения. :
:


 или
или  .
. .
.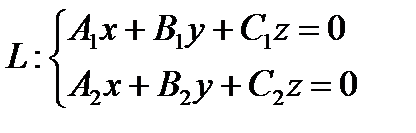





 = k называется угловым коэффициентом прямой.
= k называется угловым коэффициентом прямой.

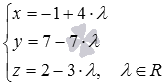 и плоскости
и плоскости  .
. :
:
 :
:
 пересекается с плоскостью
пересекается с плоскостью  , то найдите координаты точки их пересечения.
, то найдите координаты точки их пересечения. . Для нахождения ее решения используем метод Гаусса. Метод Гаусса позволит нам не только определить, имеет ли записанная система уравнений одно решение, бесконечное множество решений или не имеет ни одного решения, но и найти решения в случае их наличия.
. Для нахождения ее решения используем метод Гаусса. Метод Гаусса позволит нам не только определить, имеет ли записанная система уравнений одно решение, бесконечное множество решений или не имеет ни одного решения, но и найти решения в случае их наличия.



