
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекция вектора на ось. Свойства проекций. Правило нахождения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть в пространстве задана некоторая прямая Def 1. Осью
Пусть Если наряду с точкой Def 2. Так построенный вектор Иногда говорят, что Вектора Def 3. Такое число Таким образом Легко видеть, что Свойства проекции: Проекция вектора на ось равна произведению длины вектора
Действительно, пусть Если Если При умножении вектора на число его проекция на ось также умножается на это число:
Действительно, если Если
Проекция суммы векторов на ось равна сумме проекций слагаемых:
Действительно, это очевидно из следующих чертежей:
БИЛЕТ №10. Скалярное произведение векторов. Свойства и приложения. Проекция вектора на вектор.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Свойства. 1) 2) 3) 4) 5)
Скалярное произведение векторов, заданных своими декартовыми координатами равно сумме по парных произведений соответствующих координат сомножителей. Применение скалярного произведения. 1. 2. Определение перпендикулярности векторов, как скалярное произведение, равное нулю. 3. 4.
БИЛЕТ №11. Векторное произведение векторов. Свойства и приложения.
Векторным произведением векторов называется вектор, обозначаемый 1. Перпендикулярен двум исходным векторам. 2. Составляет с исходными векторами правую тройку[6]
3. Направление результирующего вектора определяется по правилу буравчика. Свойства векторного произведения. 1. 2. 3. 4. 5. 6.
БИЛЕТ №12. Смешанное произведение векторов. Свойства и приложения.
Смешанным произведением трёх векторов называется число, обозначаемое
1. 2. 3.
Свойства смешанного произведения. 1) 2) 3)
БИЛЕТ №13. Уравнение прямой на плоскости, проходящей через заданную точку и заданным углом.
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
БИЛЕТ №14. Уравнение прямой на плоскости, проходящей через заданную точку и заданным нормальным вектором. Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой, заданной уравнением Ах + Ву + С = 0. Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.
БИЛЕТ №15. Общее уравнение прямой. Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу • А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
БИЛЕТ №16.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.244.100 (0.008 с.) |

 и единичный вектор
и единичный вектор 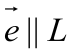 .
. (направляющий вектор оси).
(направляющий вектор оси). – точка непринадлежащая
– точка непринадлежащая 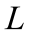 . Проведем через точку
. Проведем через точку  ⊥
⊥  . Получим точку
. Получим точку  , которая называется проекцией (ортогональной проекцией) точки
, которая называется проекцией (ортогональной проекцией) точки  на ось
на ось  . Обозначение:
. Обозначение:  .
. взять точку
взять точку  , то можно построить
, то можно построить  .
. называется векторной проекцией вектора
называется векторной проекцией вектора  на ось
на ось  . Обозначают:
. Обозначают:  .
. есть компонента вектора
есть компонента вектора  на оси
на оси  .
. и
и  – коллинеарны ⇒
– коллинеарны ⇒ 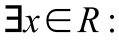
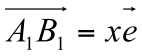 .
. называется скалярной проекцией (проекцией) вектора
называется скалярной проекцией (проекцией) вектора  на ось
на ось  . Пишут:
. Пишут:  .
. .
. , если
, если  на косинус угла между вектором и осью:
на косинус угла между вектором и осью: .
. .
. (см. рис. 1), то
(см. рис. 1), то  , поэтому
, поэтому  .
. (см. рис. 2), то
(см. рис. 2), то  , и
, и  .
. .
. , то
, то  λ и
λ и 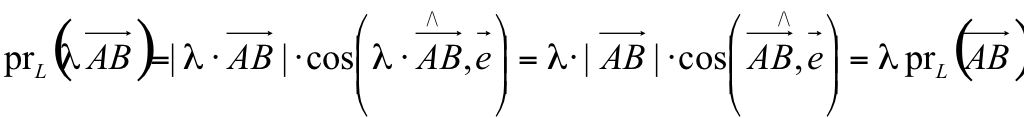 .
. , то
, то 



 .
.

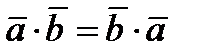 – Коммутативность.
– Коммутативность.




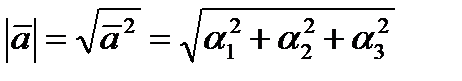


 , который обладает двумя свойствами:
, который обладает двумя свойствами:
 – проверка на колиниарности.
– проверка на колиниарности.
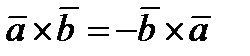




 , равное скалярному произведению трёх его сомножителей, на векторное произведение двух первых.
, равное скалярному произведению трёх его сомножителей, на векторное произведение двух первых.

 , а значит угол v – острый, следовательно, вектора составляют правую тройку.
, а значит угол v – острый, следовательно, вектора составляют правую тройку. , а значит угол v – тупой, следовательно, вектора составляют левую тройку.
, а значит угол v – тупой, следовательно, вектора составляют левую тройку.
 комплонарны.
комплонарны.
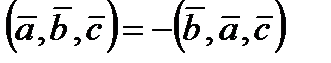


 и обозначить
и обозначить  , то полученное уравнение называется уравнением прямой с угловым коэффициентом k.
, то полученное уравнение называется уравнением прямой с угловым коэффициентом k. (3, -1).
(3, -1).


