
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие проекции вектора на ось, её свойства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1°.Для определения векторной величины, кроме чис ленного значения, необходимо знать ее направление. Примерами таких величин служат скорость и ускорение, перемещение точки при движении тела. Определение. Вектором называется направленный отрезок, то есть отрезок, у которого различают начало и конец. Начало вектора называется точкой его приложения; прямая l, на которой расположен вектор, называется линией его действия. Определение. Модулем вектора называется его длина. Модуль вектора обозначается символом |А¯В | или|а¯|. Определение. Проекцией вектора на ось называется скаляр, равный модулю составляющей вектора по этой оси, взятому со знаком плюс, если направление составляющей совпадает с направлением оси, и со знаком минус, если эти направления противоположны. Если вектор перпендикулярен оси, то его проекция равна нулю. Свойства проекции вектора на ось: 1. Проекция вектора на ось не изменяется от параллельного переноса векторов. пр l AB = прl A1B1 2. Аддитивность проекции. Проекция суммы векторов на некоторую ось равна сумме проекций данных векторов на эту ось. прl (a1+a2+a3)=прl a1+прl a2+прl a3 3. Однородность проекции. Скалярный множитель можно выносить за знак проекции вектора на ось 4. Пр.вектора на ось рав. произв. мод.вектора на косинус угла между вектором и осью прl а‾ = /а‾/ * cosφ - если угол φ острый – проекция положительная - если угол φ тупой – проекция отрицательная
6. Понятие скалярного произведения векторов. С калярная величина определяется одним числом, выражающим отношение этой величины к единице измерения. Примерами таких величин являются температура, объем, масса.Скалярным произвед двух векторов наз: скаляр, равный, произв едению модулей этих векторов и cos угла между ними. Механич смысл скалярного произведения: пусть материальная точка перемещ из точки В в точку С по прямой под действием силы
1) Коммутативный(переместительный закон)
2) ассоциативный(сочетательный) з. 3) Дистрибутивный(распределит) з. Формула для вычисления по координатам сомножителей: Координатами вектора а‾ называются его проекции ах ,ау ,аz на координатные оси. Векторное произведение двух векторов = произведению третьего порядка, у которого в первой строке находятся орты, во второй строке координаты первого вектора, в третьей строке координаты второго вектора. пример: Ответ:
ТЕОРМЕХ 1. Сила, элементы графостатики. Мера механического взаимодействия тел, т.е. взаимодействия, влияющего на их состояние покоя или движения, характеризуется силой. Сила определяется: 1числовым значением 2направлением 3точкой прилож. Таким образом, сила - величина векторная.
Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Величину, равную геометрической сумме сил какой-либо системы, называют главным вектором этой системы сил. Геометрическая сумма R гл, (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма (или треугольника) или построением силового многоугольника.
Отметим, что сила R гл не является равнодействующей системы сил, т.к. заменяет систему сил не одна, а вместе с парой М гл.
Для равновесия любой системы сил необходимо и достаточно, чтобы R гл =0 и М гл =0.
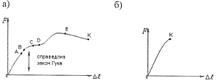
2. Хрупкость и пластичность Хрупкость -способность мат-ла разрушаться при незначит. остаточных деформациях. Пластичность -способ-ть получать значительные остат. Деформации, не разрушаясь. При проектировании строительных конструкций необходимо установить значения величин, характеризующих прочностные и деформативные свойства материалов. Наибольшую информацию о механических свойствах металлов можно получить из статических испытаний на растяжение. Записанные с помощью специального устройства диаграммы растяжения (т.е. графики зависимости между растягивающей силой F и удлинением образца ∆l) имеют вид: Первая диаграмма характерна для пластических материалов (низкоуглеродная сталь). Диаграмма имеет ряд характерных участков: ОА - зона упругости, нагрузка пропорциональна деформации; АВ - до точки В, в материале не обнаруживается признаков пластической (остаточной) деформации; CD - площадка текучести, деформации растут практически без увеличения нагрузки; BD - зона общей текучести, в этой зоне значительно развиваются пластические деформации. DE - зона упрочнения, при максимальном (или не сколько меньшем) усилии на образце в наиболее слабом месте возникает сужение - «шейка»; ЕК - зона местной текучести, деформации происходят в области «шейки» вплоть до разрыва в точке К. Вторая диаграмма характерна для хрупкого мате риала (чугуна). Диаграмма не имеет выраженного начального прямолинейного участка. Разрыв образцов из хрупких металлов происходит при весьма незначительном удлинении и без образования шейки. Диаграмма F = f (∆l) зависит от размеров образца, поэтому её перестраивают в координатах «напряжение-деформация». Напряжением называется внутренняя сила, отнесённая к единице площади в данной точке рассматриваемого сечения σ =F/A. Изменение ∆l первоначальной длины стержня l называется абсолютным удлинением. Отношение абсолютного удлинения к первоначальной длине ε = ∆ l/l называется относительным удлинением или деформацией. При упругих деформациях связь между деформациями и напряжениями линейна и описывается законом Гука: σ = Е * ε, где Е - модуль упругости.
3. Степень свободы системы. Степенью свободы системы называют наименьшее число геометрических параметров (координат точек, углов поворота элементов системы, их длины), которые могут независимо друг от друга изменяться при движении системы относительно земли. W = 3D-2Ш-3Ж-C оп -Cco6cmв W - степень свободы системы, D - количество дисков, Ш - количество шарниров,Ж - количество жёстких дисков, Соп - количество опорных стержней, Ссоб - количество собственных стержней системы. W<0. Система геометрически изменяема, она не имеет достаточного количества связей, обеспечивающих неизменяемость. Такие системы в строительстве не применяются. W > 0. Система имеет так называемые «лишние» связи, которые не являются необходимыми для обеспечения неизменяемости системы, и называется статически неопределимой. W < 0. Система геометрически неизменяемая. Статическая неопределимость может быть внешней или внутренней. В первом случае опорные реакции, а, следовательно, и внутренние усилия, не могут быть определены с помощью одних лишь уравнений статики. Во втором случае опорные реакции могут быть определены с помощью уравнений статики, а внутренние усилия - нет. W = 0. Система не имеет лишних связей, она статически определима и может быть неизменяемой. Для того, чтобы решить вопрос о пригодности использования такой системы, необходимо произвести её структурный анализ. Из-за неправильного расположения связей возможно образование так называемых «мгновенно» изменяемых систем, которые не могут быть использованы в строительстве.
4. НДС (напряженно-деформированные состояния) Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечение бруса возникает только продольная сила. N (растягивающая или сжимающая), а все остальные внутренние усилия равны нулю.
A= N / σ. Под изгибом понимают такой вид напряжения, при котором в поперечных сечениях бруса возникают изгибающие моменты. Если в поперечных сечениях бруса имеют место только изгибающие моменты — это случай чистого изгиба, если же возникают изгибающие моменты и поперечные силы - это так называемый поперечный изгиб.
Эпюры напряжений в сечениях бруса имеют вид Напряжённое состояние - чистый сдвиг. В поперечных сечениях возникают только касательные напряжения τ. Подбор сечения осуществляется по формуле:Под сложным сопротивлением подразумевают комбинации простых напряженных состояний (растяжения, сжатия, сдвига, кручения и изгиба.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.6.179 (0.013 с.) |

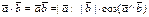 Пример: найти
Пример: найти 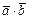 , если
, если 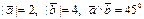 решение:
решение: 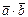
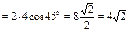
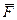
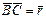 - вектор перемещения. Как известно при этом совершается работа А,
- вектор перемещения. Как известно при этом совершается работа А, 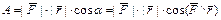
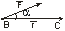
 - скалярное перемещени Если материальная точка перем. прямолинейно под действием некоторой силы, то скалярное произведение силы на вектор перемещения = совершаемой при этом работе. Свойства скалярного произведения:
- скалярное перемещени Если материальная точка перем. прямолинейно под действием некоторой силы, то скалярное произведение силы на вектор перемещения = совершаемой при этом работе. Свойства скалярного произведения: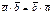

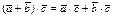
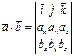
 ,
, 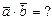 решение:
решение: 
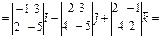
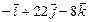
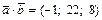
 Системой сил будем называть совокупность сил, действующих на одно рассматриваемое тело. Различают системы сходящихся, параллельных и произвольно-расположенных сил.
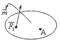
Системой сил будем называть совокупность сил, действующих на одно рассматриваемое тело. Различают системы сходящихся, параллельных и произвольно-расположенных сил. Равнодействующая системы сходящихся сил находится непосредственно с помощью закона параллелограмма сил. Аналогичную задачу можно решить и для произвольной системы сил, если найти возможность перенести все силы в одну точку. Такая возможность существует. Перенесем силу F из точки А в точку В.
Равнодействующая системы сходящихся сил находится непосредственно с помощью закона параллелограмма сил. Аналогичную задачу можно решить и для произвольной системы сил, если найти возможность перенести все силы в одну точку. Такая возможность существует. Перенесем силу F из точки А в точку В. Полученная при этом система трёх сил и представляет собой силу F 1 = F, но приложенную в точке В, и пару F,F 2. (Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело). Таким образом, система произвольно расположенных сил при приведении к произвольно выбранному центру эквивалента одной силе Rгл (главному вектору), приложенной в центре приведения, и одной паре Мгл (главному моменту).
Полученная при этом система трёх сил и представляет собой силу F 1 = F, но приложенную в точке В, и пару F,F 2. (Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело). Таким образом, система произвольно расположенных сил при приведении к произвольно выбранному центру эквивалента одной силе Rгл (главному вектору), приложенной в центре приведения, и одной паре Мгл (главному моменту).
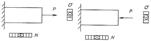 При центральном растяжении (сжатии) в поперечном сечении возникают только нормальные напряжения σ=N/A Подбор сечения осуществляется по формуле
При центральном растяжении (сжатии) в поперечном сечении возникают только нормальные напряжения σ=N/A Подбор сечения осуществляется по формуле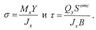


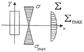
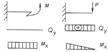 Во всех точках поперечного сечения бруса возникают нормальные σ и касательные τ напряжения, которые могут быть определены по формулам:
Во всех точках поперечного сечения бруса возникают нормальные σ и касательные τ напряжения, которые могут быть определены по формулам: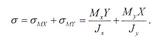 Изгиб называют косым, если плоскость действия изгибающего момента, не совпадает ни с одной из его главных плоскостей. Косой изгиб можно рассматривать как совокупность двух прямых изгибов во взаимно перпендикулярных плоскостях. При косом изгибе в поперечных сечениях бруса в общем случае возникают 4 внутренних силовых фактора Qx, Mx, Qy u My.
Изгиб называют косым, если плоскость действия изгибающего момента, не совпадает ни с одной из его главных плоскостей. Косой изгиб можно рассматривать как совокупность двух прямых изгибов во взаимно перпендикулярных плоскостях. При косом изгибе в поперечных сечениях бруса в общем случае возникают 4 внутренних силовых фактора Qx, Mx, Qy u My.


