
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторное и смешанное произведения векторовСодержание книги
Поиск на нашем сайте
16. Найти координаты единичного вектора (орта) 17. Два вектора а) ортов б) вектора в) вектора 18. Найти проекцию вектора 19. Найти проекцию вектора 20. В выпуклом четырехугольнике ABCD диагонали АС и ВD пересекаются в точке О. Известно, что а) ввести декартову прямоугольную систему координат ХОУ с началом в точке О так, чтобы ось Ох была направлена по диагонали АС (построение четырехугольника нужно начинать с построения диагоналей АС и ВD, причем диагональ АС удобнее расположить горизонтально); б) найти в этой системе координаты точек А,В,С,D; в) найти координаты векторов г) найти д) подсчитать искомый угол по формуле 21. Найти координаты вектора 22. Дано 23. Вычислить координаты векторного произведения 24. Даны вершины треугольника А(2,3,1), В(1,1,-2) и С(2,0,-2). Найти площадь треугольника и длину высоты, опущенной из вершины А. 25. Вычислить 26. Вектор 27. Вычислить смешанное произведение векторов 28.Установить, компланарны ли векторы 29. Вычислить объем пирамиды, вершины которой: А(10,6,6), В(-2,8,2), С(6,8,9), D(7,10,3). 30. Вектор
4. Аналитическая геометрия в пространстве: плоскость и прямая в пространстве; Поверхности второго порядка
31. Составить уравнение плоскости, проходящей через точку
32. Составить уравнение плоскости, проходящей через точку 33. Составить уравнение плоскости, проходящей через прямую 34. Составить уравнение плоскости, которая проходит через точку 35. Найти расстояние 36. На оси Оу найти координаты точек, отстоящих от плоскости
37. Даны вершины треугольника А(1-2,-2), В(3,-1,0), С(-3,2,2). Составить канонические уравнения биссектрисы его внутреннего угла при вершине В. 38. Составить канонические уравнения прямой, проходящей через точку 39. Найти координаты точки пересечения прямой 40. Найти проекцию точки Р(4,1,5) на прямую х=3t+2; у=5t-5; z=2t+4. 41. Найти координаты точки Q, симметричной точке Р(4,6,-1) относительно плоскости 42. Найти координаты точки Q, симметричной точке Р(2,5,-2) относительно плоскости 43. Вычислить расстояние 44. Составить уравнение прямой l, которая проходит через точку М0 (1,4,-1) перпендикулярно вектору а) составить уравнение плоскости П, проходящей через точку М0 с нормальным вектором б) найти координаты точки М1 пересечение прямой l1 с плоскостью П (см. задачу 39); в) составить кононические уравнения прямой, проходящей через точки М0 и М1. 45. Даны координаты вершины пирамиды А1(2,2,4), А2(4,2,2), А3(3,3,4), А4(5,1,3). Найти: 1) угол между ребрами А1А2 и А1А4; 2) угол между ребром А1А4 и гранью А1А2А3; 3) уравнение прямой А1А2; 4) уравнение плоскости А1А2А3; 5) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. 46. Построить эскиз тела, ограниченного поверхностями: а) б) х=0, у=0, z=0,
5. Элементы линейной алгебры: метод гаусса. решения системы линейных уравнений; формулы крамера; матрицы; мАтричные уравнения; линейное векторное пространство; линейная зависимость (независимость) системы векторов; линейные операторы; собственные векторы и собственные значения линейного оператора
47. Решить систему линейных уравнений методом Гаусса:
48. Найти все вещественные матрицы, перестановочные с матрицей 49. Найти матрицу А= 50. Найти ранг матриц: а) 51. Дана система линейных уравнений
Доказать ее совместность и решить тремя способами: а) методом Гаусса; б) средствами матричного исчисления; в) по формулам Крамера. 52. Является ли вещественным линейным пространствоми: а) множество всех векторов из арифметичекого пространства R4 вида (а;0;0;в)? б) множество всех векторов из арифметического пространства R4 вида (а;1;1;в)?
53. Найти все значения 54. Выяснить, является ли данная система векторов из 55. Выяснить геометрический смысл действия линейных операторов, данных в пространстве R3, матрицы которых относительно некоторого прямоугольника имеют вид: а) 56. Является ли оператор 57. Линейный оператор 58. Найти собственные значения и собственные векторы линейного преоразования, заданного в некотором базисе матрицей
ответы: 1. 7. 23. 25. 37. 2) 4) 48. 49.
52. а) да, б) нет. 53.
57.
Вариант 6
1. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ: ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ; ПРЯМАЯ НА ПЛОСКОСТИ; ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
1. Доказать, что точки А(2,2), В(-1,6), С(-5,3) и D(-2,-1) являются вершинами квадрата. 2. Даны вершины треугольника А(1;-1), В(-2;-1), С(3;5). Составить уравнения перпендукуляра, опущенного из вершины А на медиану, проведеную из вершины В. 3.Найти координаты точки М1, симметричной точке М2(6;-3) относительно прямой, проходящей через точки А(1;2) и В(2,-3). 4. Даны две смежные вершины параллелограмма А(-3,3), В(1,5) и точка пересечения его диаганалей М(1;1). Определить координаты двух других вершин. 5. Отрезок, ограниченный точками А(2;-5) и В(-1,-2), разделен на три равные части. Определить координаты точек деления. 6. Даны уравнения двух сторон прямоугольника 5х+2у-7=0, 5х+2у - 36=0 и уравнения его диагонали 3х+7у-10=0. Составить уравнения остальных сторон и второй диагонали этого прямоугольника. 7. Даны две вершины А(-4;2) и В(4,-2) и точка D(3,2) пересечение высот треугольника. Составить уравнения его сторон. 8. Найти расстояние от точки М(-4;2) до прямой, проходящей через точки А(-1,2) и В(1,6), 9. Установить, какие линии определяются в полярных координатах следующими уравнениями (построить их на чертеже):
а) д) 10. Установить, какая линия определяется уравнением 11. Точка М1(2,-2) является концом малой оси эллипса, фокусы которого лежат на прямой у+7=0. Составить уравнение этого эллипса, зная его эксцентриситет 12. Составить уравнение линии, каждая точка которой равноудалена от точки А(1,5) и от прямой 13. Линия задана уравнением Требуется: а) построить линию по точкам, начиная от б) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; в) по полученному уравнению определить, какая это линия.
2. Определители. Базис в пространстве. Координаты вектора
14. Вычислить определители: а) по правилу треугольника; б) разложением по элементам первой строки; в) разложением по элементам второго столбца; г) сведением к треугольному виду:
а)
15. Даны векторы:
3. Линейные операции над векторами. Проекция вектора на ось.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.190.247 (0.01 с.) |

 , сонаправленного с вектором
, сонаправленного с вектором  =(2,-3,-6).
=(2,-3,-6). =(–2,3,6) приложены к одной точке. Найти координаты:
=(–2,3,6) приложены к одной точке. Найти координаты: векторов
векторов 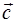 , направленного по биссектрисе угла между векторами
, направленного по биссектрисе угла между векторами  .
. =(5;3;-1) на направление вектора
=(5;3;-1) на направление вектора  .
. =(2,–3,-5) на ось, составляющую с координатными осями равные тупые углы.
=(2,–3,-5) на ось, составляющую с координатными осями равные тупые углы. .Найти величену угла между векторами
.Найти величену угла между векторами 
 и
и 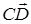 используя последовательность действий:
используя последовательность действий:
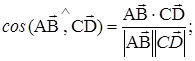

 , если
, если  где
где 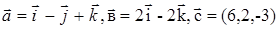 .
. Найти
Найти  и
и 
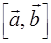 и его длину
и его длину  , если
, если  (i-3k).
(i-3k). если
если  .
. ортогонален векторам
ортогонален векторам 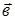 =(-1,3,-1) и составляет с осью Оу тупой угол. Найти координаты вектора
=(-1,3,-1) и составляет с осью Оу тупой угол. Найти координаты вектора  , если
, если  и
и 


 перпендикулярен к векторам
перпендикулярен к векторам 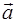 и
и  , если
, если 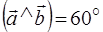 ,
,  ,
, 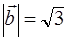 ,
,  , а тройка векторов
, а тройка векторов  – правая.
– правая. , параллельную плоскости
, параллельную плоскости  .
. и прямую
и прямую  .
. , перпендикулярно плоскости
, перпендикулярно плоскости  .
.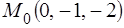 , перпендикулярно двум плоскостям:
, перпендикулярно двум плоскостям:  и
и  .
. от точки
от точки  до плоскости
до плоскости  .
.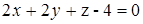 на расстоянии d=2.
на расстоянии d=2. , параллельно прямой
, параллельно прямой  ,
,  ,
,  .
. и плоскости
и плоскости  .
. .
. .
. .
. и пересекает прямую l1:
и пересекает прямую l1:  используя последовательность действий:
используя последовательность действий: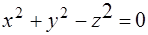 ,
, 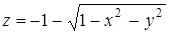
 , x+y=1
, x+y=1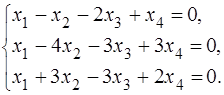
 .
. , где
, где , В=
, В=  , С=
, С=  .
. ; б)
; б)  .
.
 , при которых вектор
, при которых вектор 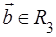 линейно выражается через векторы
линейно выражается через векторы  , если
, если  =(1, 2, 3),
=(1, 2, 3), 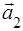 =(2, 1, 3),
=(2, 1, 3),  =(3, 5, 8).
=(3, 5, 8). линейно зависимой?
линейно зависимой?  ; б)
; б)  .
. где
где  линейным? Если да, найт его матрицу в базисе (
линейным? Если да, найт его матрицу в базисе (
 на плоскости XOY зеркально отрожает все векторы относительно оси ОХ, а линейный оператор
на плоскости XOY зеркально отрожает все векторы относительно оси ОХ, а линейный оператор  проецирует все векторы плоскости на прямую у=
проецирует все векторы плоскости на прямую у=  . Найти матрицы операторов
. Найти матрицы операторов  и
и 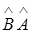 в базисе (
в базисе (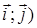 .
. .
. . 2. Уравнение медианы: 4х-у-22=0; уравнение высоты: 3х-2у-19=0. 3. М1(8;-3). 4.Д(-4;0). 5.(4; -1) и (5;1). 6. 4х-у-10=0, х-4=0, х+8у+14=0.
. 2. Уравнение медианы: 4х-у-22=0; уравнение высоты: 3х-2у-19=0. 3. М1(8;-3). 4.Д(-4;0). 5.(4; -1) и (5;1). 6. 4х-у-10=0, х-4=0, х+8у+14=0. ,
,  ,
,  , 8. 45 кв.ед. 9. 1) окружность с центром в полюсе и радиусом 6. 2) луч, выходящий из полюса, наклоненный к полярной оси под углом 3\4
, 8. 45 кв.ед. 9. 1) окружность с центром в полюсе и радиусом 6. 2) луч, выходящий из полюса, наклоненный к полярной оси под углом 3\4  . 3) прямая, перпендикулярная к полярной оси, отсекающая на ней, считая от полюса, отрезок а=6; 4) прямая, расположенная в верхней полуплоскости, параллельная полярной оси, отстоящая от нее на расстоянии равном 5. 5) окружность с центром
. 3) прямая, перпендикулярная к полярной оси, отсекающая на ней, считая от полюса, отрезок а=6; 4) прямая, расположенная в верхней полуплоскости, параллельная полярной оси, отстоящая от нее на расстоянии равном 5. 5) окружность с центром  и радиусом 5. 6) окружность с центром
и радиусом 5. 6) окружность с центром  и радиусом 6. 10. Гипербола
и радиусом 6. 10. Гипербола  ,
,  , полуоси
, полуоси  ,
,  ,
, 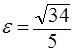 . 11.
. 11. 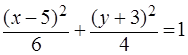 . 12. Парабола: (у+2)2=8(х+5). 13. в) Правая ветвь гиперболы
. 12. Парабола: (у+2)2=8(х+5). 13. в) Правая ветвь гиперболы  . 14. а) -11, б) -52, в) –9, г) -8. 15.
. 14. а) -11, б) -52, в) –9, г) -8. 15.  . 16.
. 16.  . 17. а)
. 17. а)  ,
,  ,б)
,б)  , в)
, в)  . 18.
. 18.  19. 2
19. 2  . 20.arccos(
. 20.arccos(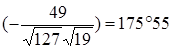 . 21.
. 21.  . 22.
. 22.  .
. ,
, 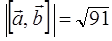 . 24.
. 24.  ,
,  .
. . 26.
. 26.  (-3,-3,-6). 27. -10. 28. Компланарны. 29. V=33 куб.ед.. 30. 18. 31.
(-3,-3,-6). 27. -10. 28. Компланарны. 29. V=33 куб.ед.. 30. 18. 31.  . 32.
. 32.  . 33.
. 33.  . 34.
. 34. 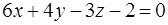 . 35.
. 35.  . 36. (0,-1,0), и (0,5,0).
. 36. (0,-1,0), и (0,5,0).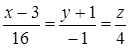 . 38.
. 38. 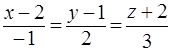 . 39.(1,6,1). 40.(5,0,6). 41. Q(-2,3,4). 42. Q(2,-3,6). 43.
. 39.(1,6,1). 40.(5,0,6). 41. Q(-2,3,4). 42. Q(2,-3,6). 43.  . 44.
. 44. 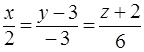 . 45. 1)
. 45. 1)  ,
, , 3)
, 3) 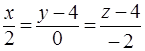 ,
,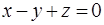 , 5)
, 5)  . 47.
. 47.  , где
, где  .
. , где
, где  .
.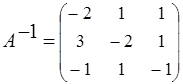 ,
,  ,
,  ,
, . 50. а)
. 50. а) 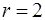 , б)
, б) 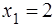 ,
,  ,
,  .
. . 54. нет. 55. а) проектирование векторов на плоскость хОу,с последующим отражением векторов – проекций относительно начала координат; б) отражение относительно начала координат. 56. Оператор
. 54. нет. 55. а) проектирование векторов на плоскость хОу,с последующим отражением векторов – проекций относительно начала координат; б) отражение относительно начала координат. 56. Оператор  линейный;
линейный; – его матрица в базисе (
– его матрица в базисе (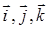 ).
). ,
,  . 58. Собственные значения:
. 58. Собственные значения:  ,
,  . Собственные векторы: для
. Собственные векторы: для 
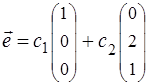 , где
, где  , - любые вещественные числа, не равные одновременно нулю; для
, - любые вещественные числа, не равные одновременно нулю; для 
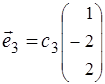 , где
, где  .
.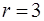 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; е)
; е)  .
. . Найти координаты ее центра, полуоси, эксцентриситет. Сделать чертеж.
. Найти координаты ее центра, полуоси, эксцентриситет. Сделать чертеж. .
. . Определить, какая это линия; сделать чертеж.
. Определить, какая это линия; сделать чертеж. в полярной системе координат.
в полярной системе координат. до
до  и придавая
и придавая  значения через промежуток
значения через промежуток  ;
; , б)
, б)  , в)
, в)  , г)
, г)  .
. 1=(-1,2,1);
1=(-1,2,1); 


