
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторы и собственные значенияСодержание книги
Поиск на нашем сайте
Линейного оператора
47. Решить систему линейных уравнений методом Гаусса: x1-2x2+x3-x4=0; x1-x2+2x3+2x4=0; 2x1+x2-2x3+x4=0 48. Найти все вещественные матрицы, перестановочные с матрицей: 49. Найти матрицу 3ВА-1+2СВТ, где А= 50. Найти ранги матриц: а)
51. Дана система линейных уравнений: x1+8x2+5x3=9: 2x1-4x2-3x3=-1; -x1+9x2+4x3=1
Доказать ее совместимость и решить тремя способами: 1) методом Гаусса, 2) средствами матричного исчесления, 3) по формулам Камера.
52. Являются ли вещественными линейными пространствами: а) множество всех векторов из арифметического пространства R4 вида (О; а; в, с)? б) множество всех векторов из арифметического пространства R4 вида (2; а, в, с)?
53. Найти все значения 54. Выяснить, является ли даная система векторов из R4 линейно зависимой?
55. Выяснить геомтрический смысл действия линейных операторов, данных в пространстве R3 матрицы которых оносительно некоторого прямоугольного базиса имеют вид: а)
56. Является ли оператор 57. Линейный оператор 58. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей
ОТВЕТЫ:
1. 2. (8,-7). 4. D(-1,2). 5. (3,0) и (4,2). 6. 4х-у-7=0, х-4=0, х+8у-10=0. 7. х+3у+3=0, 3х-у+7=0, 3х-у-5=0. 8. 125 кв. ед. 9. 1) окружность с центром в полюсе и радиусом 3; 2) луч, выходящий из полюса, наклоненный к полярной оси под углом полуоси: а=2, в=3, 25. 34. x+2y-z-9=0. 35.
38. 55. а) отражение относительно плоскости ХОZ, б) растяжение в два раза вдоль оси ОУ. 56. Оператор 57. для
ВАРИАНТ 3
1. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ: ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ; ПРЯМАЯ НА ПЛОСКОСТИ; ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
1. Доказать, что треугольник с вершинами А1(0;3), А2(1;5), А3(4;1) прямоугольный. 2. Даны вершины треугольника А(3;-1), В(-1;-3), С(5;-7). Составить уравнения его медианы и высоты, проведенных из вершины А. 3.Найти координаты точки М1, симметричной точке М2(4;-5) относительно прямой, проходящей через точки А(-1;0) и В(-5;2). 4. Даны три вершины параллелограмма А(4;-3), В(6;-1), С(0;5). Определить координаты четвертой вершины D, противоположной В. 5. Отрезок, ограниченный точками А(0;-4) и В(3;2), разделен на три равные части. Определить координаты точек деления. 6. Даны две вершины А(3;-3), В(5;5) треугольника АВС и точка N(4;-3) пересечениия его высот. Составить уравнения сторон этого треугольника. 7. Уравнение одной из сторон квадрата x+3y-1=0. Составить уравнения трех остальных сторон квадрата, если (-2;-1) – точка пересечения его диагоналей. 8. Точка А(3;-7) является вершиной квадрата, одна из сторон которого лежит на прямой: 3 9. Установить, какие линии определяются в полярных координатах следующими уравнениями (построить их на чертеже): а) б) 10. Установить, какая линия определяется уравнением 11. Точка М1(1,-3) является концом малой оси эллипса, фокусы которого лежат на прямой у+7=0. Составить уравнение этого эллипса, зная его эксцентриситет 12. Составить уравнение линии, каждая точка которой равноудалена от точки А(-2,-4) и от прямой 13. Линия задана уравнением Требуется: а) построить линию по точкам, начиная от
2. Определители. Базис в пространстве. Координаты вектора
14. Вычислить определители: а) по правилу треугольника; б) разложением по элементам первой строки; в) разложением по элементам второго столбца; г) сведением к треугольному виду:
а)
15. Даны векторы:
3. Линейные операции над векторами. Проекция вектора на ось.
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.143.57 (0.01 с.) |

 .
.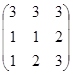 , В=
, В=  , С=
, С= 
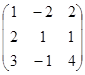 б)
б) 
 , при которых вектор
, при которых вектор  линейно выражается через векторы
линейно выражается через векторы  , если
, если 


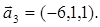


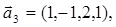

 б)
б) 
 где
где  ,
,  линейным? Если да, найти его матрицу в базисе
линейным? Если да, найти его матрицу в базисе  .
. на плоскости ХОУ зеркально отражает все векторы относительно оси ОХ, а линейный оператор
на плоскости ХОУ зеркально отражает все векторы относительно оси ОХ, а линейный оператор  проецирует все векторы плоскости на прямую
проецирует все векторы плоскости на прямую  . Найти матрицы операторов
. Найти матрицы операторов  и
и  в базисе
в базисе  .
.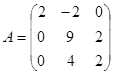
 . 2. Уравнение медианы: 4х–у–10=0, уравнение высоты: 3х–2у–5=0.
. 2. Уравнение медианы: 4х–у–10=0, уравнение высоты: 3х–2у–5=0. ; 3) прямая, перпендикулярная к полярной оси, отсекающая на ней, считая от полюса, отрезок а =3; 4) прямая, расположенная в верхней полуплоскости, параллельная полярной оси, отстоящая от неее на расстоянии равном 2; 5) окружность с центром
; 3) прямая, перпендикулярная к полярной оси, отсекающая на ней, считая от полюса, отрезок а =3; 4) прямая, расположенная в верхней полуплоскости, параллельная полярной оси, отстоящая от неее на расстоянии равном 2; 5) окружность с центром  r = 1) и радиусом 1; 6) окружность с центром
r = 1) и радиусом 1; 6) окружность с центром  r = 2) и радиусом 2. 10. Гипербола:
r = 2) и радиусом 2. 10. Гипербола: 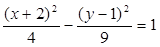 , С(-2,1)
, С(-2,1) . 11.
. 11.  . 12. Парабола: (у-1)2=12(х-1). 13. Левая ветвь гиперболы:
. 12. Парабола: (у-1)2=12(х-1). 13. Левая ветвь гиперболы:  . 14. а) -26, б) –30 в) –18, г) 8. 15. в=(2,3,1). 16.
. 14. а) -26, б) –30 в) –18, г) 8. 15. в=(2,3,1). 16.  . 17. а)
. 17. а)  ,
, 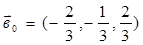 , б)
, б) 
 , в)
, в)  . 18.
. 18. 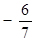 . 19.
. 19.  . 20.
. 20.  . 21.
. 21.  . 22.
. 22. 
 . 23.
. 23.  ,
,  . 24.
. 24.  ,
, 
 . 26.
. 26.  . 27. 11. 28. Компланарны. 29.
. 27. 11. 28. Компланарны. 29.  . 30.
. 30.  . 31. x+2у+2z=0. 32. 13х-10у-z-7=0. 33. 11x-10y-4z-52=0.
. 31. x+2у+2z=0. 32. 13х-10у-z-7=0. 33. 11x-10y-4z-52=0. . 36. (0,-10,0) и (0,8,0). 37.
. 36. (0,-10,0) и (0,8,0). 37.  .
.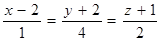 . 39. (1, 4, -13). 40. (3,3,2). 41. (4,10,-1). 42. (-2,-6,-1). 43. 3. 44.
. 39. (1, 4, -13). 40. (3,3,2). 41. (4,10,-1). 42. (-2,-6,-1). 43. 3. 44.  . 45. 1)
. 45. 1) 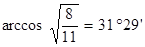 , 2)
, 2)  ,
,  , 4) х-у+z-3=0, 5)
, 4) х-у+z-3=0, 5)  . 47.
. 47. 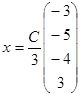 , где
, где 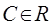 . 48.
. 48.  где
где  . 49.
. 49.  ,
,  ,
,  ,
,  . 50. а)
. 50. а) 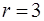 , б)
, б)  ,
,  ,
,  . 52. а) да, б) нет. 53.
. 52. а) да, б) нет. 53.  . 54. да.
. 54. да. линейный;
линейный;  – его матрица в базисе
– его матрица в базисе  .
.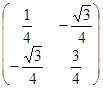 ,
,  . 58. Собственные значения:
. 58. Собственные значения:  ,
,  ,
,  , собственные векторы: для
, собственные векторы: для  ,
, 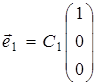 , где
, где  ,
, , где
, где  , для
, для  , где
, где  .
. . Вычислить площадь квадрата.
. Вычислить площадь квадрата.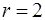 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; е)
; е)  .
. . Найти координаты ее центра, полуоси, эксцентриситет. Сделать чертеж.
. Найти координаты ее центра, полуоси, эксцентриситет. Сделать чертеж.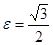 .
. . Определить, какая это линия; сделать чертеж.
. Определить, какая это линия; сделать чертеж. в полярной системе координат.
в полярной системе координат. до
до  и придавая
и придавая  значения через промежуток
значения через промежуток  ; б) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; в) по полученному уравнению определить, какая это линия.
; б) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; в) по полученному уравнению определить, какая это линия. , б)
, б)  , в)
, в)  , г)
, г) 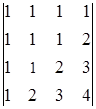 .
. 1=(7,4,8);
1=(7,4,8);  2=(1,9,3);
2=(1,9,3);  =(-13,1,-13) в некотором базисе. Показать, что первые три вектора сами образуют базис и найти координаты вектора
=(-13,1,-13) в некотором базисе. Показать, что первые три вектора сами образуют базис и найти координаты вектора 


