
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие задачи аналитической геометрииСодержание книги
Поиск на нашем сайте
НА ПЛОСКОСТИ; ПРЯМАЯ НА ПЛОСКОСТИ; ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ.
1.Доказать,что треугольник с вершинами А1(3,0), А2(4,2), А3(7,-2) прямоугольный. 2.Даны вершины треугольника А(3,2), В(-1,0), С(5,-4). Составить уравнения его медианы и высоты, проведенных из вершины А. 3.Найти координаты точки М1, симметричной точке М1(6,-11) относительно прямой, проходящей через точки А(1,-6), В(-3,-4). 4.Даны три вершины параллелограмма А(5,-4), В(7,-2), С(1,4). Определить координаты четвертой вершины D, противоположной В. 5.Отрезок, ограниченный точками А(2,-2), В(5,4) разделен на три равные части. Определить координаты точек деления. 6.Даны две вершины А(2,1), В(4,9) треугольника АВС и точка N(3,1) пересечения его высот. Составить уравнения сторон этого треугольника. 7.Уравнение одной из сторон квадрата х+3у-9=0. Составить уравнения трех остальныхсторон квадрата, если (0,1) - точка пересечения его диагоналей. 8.Точка А(3,-4) является вершиной квадрата, одна из сторон которого лежит на прямой х-2у+8=0. Вычислить площадь квадрата. 9.Установить, какие линии определяются в полярных координатах следующими уравнениями (построить их на чертеже): 1) 3) 10 Установить, какая линия определяется уравнением 11.Точка М1(2,3) является концом малой оси элипса, фокусы которого лежат на прямой у+2=0. Составить уравнение этого элипса, зная его эксцентриситет 12.Составить уравнение линии, каждая точка которой равноудалена от точки А(4,1) и от прямой х+2=0. Определить какая эта линия. Сделать чертеж. 13.Линия задана уравнением а) построить линию по точкам, начиная от б) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совподает с плюсом, а положительная полуось абсцисс – с полярной осью; в) по полученному уравнению определить, какая это линия.
2. ОПРЕДЕЛИТЕЛИ. БАЗИС В ПРОСТРАНСТВЕ. КООРДИНАТЫ ВЕКТОРА
14.Вычислить определители: а) по правилу треугольника; б) разложением по элиментам первой строки; в) разложением по элиментам второго столбца; г) сведением к треугольному виду: а)
15. Даны векторы:
3. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ, ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ. СКАЛЯРНОЕ, ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
16. Найти коородинаты еденичного вектора (орта) 17. Два вектора а) ортов б) вектора в) вектора 18. Найти проекцию вектора 19. Найти проекцию вектора 20. В выпуклом четырехугольнике АВСD диагонали АС и ВD пересекаются в точке О. Известно, что Найти величину угла между векторами а) ввести декартовую прямоугольную систему координат ХОУ с началом в точке О так, чтобы ось Ох была направлена по диагонали б) найти в этой системе координаты точек А,В,С,D; в) найти координаты векторов г) найти д) подсчитать искомый угол по формуле 21. Найти координаты вектора 22. Дано 23. Вычеслить координаты векторного произведения 24. Даны вершины треугольника А(5,-6,2), В(1,-1,2), С(1,3,-1). Найти площадь треугольника и длину высоты, опущенной из вершины А. 25. Вычислить 26. Вектор 27. Вычислить смешанное произведение векоров 28. Установить, компланарны ли векторы 29. Вычислить объем пирамиды, вершины которой: А(3,4,2), В (5,2,-1), С(7,4,8), D(-4,-3,7). 30. Вектор
4.аналитическая геометрия в пространстве: плоскость и прямая в прстранстве; Поверхности второго порядка
31. Составить уравнение плоскости, проходящей через точку М0(2,-1,0), параллельную плоскости: x+2y+2z+1=0. 32. Составить уравнение плоскости, проходящей через точку М0(2,2,-1) и прямую: 33. Составить уравнение плоскости, проходящей через прямую 34. Составить уравнение плоскости, которая проходит через точку М0(2,2,-3) перпендикулярно двум плоскостям: 2x-y+5=0 и 3x-2y-z+1=0. 35. Найти расстояние d точки М0(3,-1,-1) до плоскости x+2y-2y-2z+7=0. 36. На оси Oy найти координаты точек, отстоящих от плоскости 2x-y+2z-1=0 на расстоянии d=3. 37. Даны вершины треугольника А(3,-1,-1), В (1,2,-7), С (3,3,-5). Составить канонические уравнения биссектрисы его внутреннего угла при вершине В. 38. Составить канонические уравния прямой, проходящей через точку М0(2,-2,-1), параллельной прямой x=t, y=4t+3, z=2t-1. 39. Найти координаты точки пересечения прямой 40.-Найти проекцию точки Р(1,2,-1) на прямую x=t+2, y=7t-4, t=-3t+5. 41. Найти координаты точки Q, симметричной точке Р(2,-4,5) относительно плоскости x+7y-3t-18=0. 42. Найти координаты точки Q, симметричной точке Р(0,8,-7) относительно прямой 43.Вычеслить расстояние d точки Р(1,2,-2) от прямой 44.Составить уравнение прямой l, которая проходит через точку М0(2,-1,3) перпендикулярно вектору используя последовательность cmb действий: а) составить уравнение плоскости П, прроходящей черезточку М0 с нормальным вектором б) найти координаты точки М1 пересечение прямой с плоскостью П (см. задачу 39); в) составить каноническое уравнение прямой, проходящей через точки М0 и М1. 45. Даны координаты вершин пирамиды А1(2,4,5), А2(4,4,3), А3(3,5,5), А4(5,3,4). Найти: 1) угол между ребрами А1,А2 и А1А4; 2) угол между ребрами А1А4 и гранью А!А2А3; 3) уравнение прямой А1А2; 4) уравнние плоскости А1А2А3; 5) уравень высоты, опущенной из вершины А4 на грань А1А2А3. 46.Построить эскиз тела, ограниченного поверхностями: а) z=2-y2, z-x=0, z+x=0; б) z=x2+y2, z=2x2+2y2, x2+y2=4.
5. элЕменты линейной алгебры: метод гаусса, решения системы линейных уранений; формулы крамера; матрицы; матричные уравнения; линейное векторное пространство; линейная зависимость (независимость) системы векторов; линейные операторы; собственные
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.205.182 (0.007 с.) |

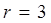 ; 2)
; 2) 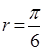 ;
;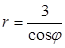 ; 4)
; 4) 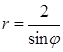 ; 5)
; 5) 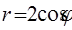 ; 6)
; 6) 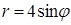 .
.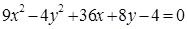 .Найти координаты ее центра, полуоси, эксцентриситет. Сделать чертеж.
.Найти координаты ее центра, полуоси, эксцентриситет. Сделать чертеж.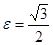 .
.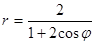 в полярной системе координат. Требуется:
в полярной системе координат. Требуется: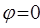 до
до  и придавая
и придавая  значения через промежуток
значения через промежуток 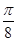 ;
;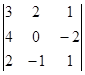 б)
б) 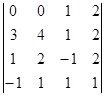 в)
в) 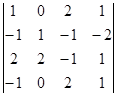 г)
г) 
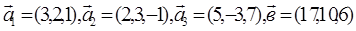 в некотором базисе. Показать, что первые три вектора сами образуют базис и найти координаты вектора
в некотором базисе. Показать, что первые три вектора сами образуют базис и найти координаты вектора 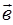 в этом базисе.
в этом базисе. 0, сонаправленного с вектором
0, сонаправленного с вектором 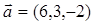 .
.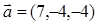 и
и  приложены к одной точке. Найти координаты:
приложены к одной точке. Найти координаты: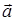 и
и  0 векторов
0 векторов 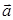 и
и 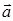 0+
0+  0;
0;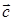 , направленного по биссектрисе угла между векторами
, направленного по биссектрисе угла между векторами 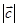 =15
=15 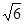 .
. на направление вектора
на направление вектора 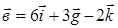 .
.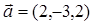 на ось, составляющую с координатными осями равные тупые углы.
на ось, составляющую с координатными осями равные тупые углы.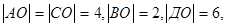
 .
.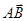 и
и 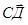 , используя последовательность действий:
, используя последовательность действий: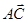 (построение четырехугольника нужно ничинать с построения диагонали АС и BD, причем диагональ АС удобнее расположить горизонтально);
(построение четырехугольника нужно ничинать с построения диагонали АС и BD, причем диагональ АС удобнее расположить горизонтально);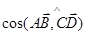 по формуле
по формуле 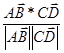 ;
;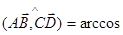
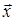 , если
, если  и пр
и пр 
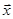 =-44, где
=-44, где 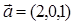 ,
, 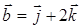 ,
,  .
.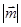 =2,
=2, 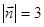 , (
, (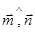 )=
)= 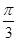 ,
, 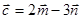 . Найти
. Найти 
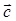 .
.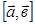 и его длину
и его длину 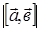 , если
, если 
 .
.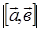 , если
, если  =2,
=2, 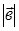 =3, (
=3, ( )= 3
)= 3 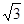 .
.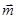 ортогонален векторам
ортогонален векторам 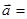 (2,1,3) и
(2,1,3) и 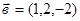 и составляет с осью Oу тупой угол. Найти координаты вектора
и составляет с осью Oу тупой угол. Найти координаты вектора 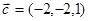 и
и 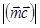 =10.
=10.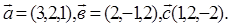
 ,
, 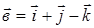 ,
, 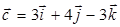 .
. , если (
, если (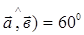 ,
, 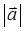 =
= 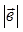 = 2,
= 2, 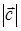 =2, а тройка векторов
=2, а тройка векторов  - правая.
- правая.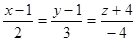 .
. перпендикулярно плоскости 2x+y+3z-2=0.
перпендикулярно плоскости 2x+y+3z-2=0. и плоскости 2x+3y+z-1=0.
и плоскости 2x+3y+z-1=0. .
.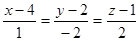 .
. и пересекат прямую l1:
и пересекат прямую l1: 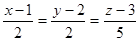
 ;
;


