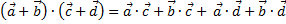Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекция вектора на ось. Их свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть
пр L
Радиус-вектор – вектор, начало которого находится в начале координат. Имеет координаты: Углом между Теорема: проекция вектора на ось равна произведению длины вектора на косинус угла между ними.
Направляющие косинусы – косинусы углов, которые вектор составляет с осями координат.
Теорема: проекция суммы векторов на ось равно сумме проекций этих векторов на эту ось. Теорема: расстояние между двумя точками равно квадратному корню из суммы квадратов разностей соответствующих координат.
Теорема: при умножении вектора
Теорема: для того, чтобы два вектора были равны, необходимо и достаточно, чтобы их проекции на любую ось были равны.
Линейная зависимость и независимость векторов. Базис пространства Пусть имеется n-векторов
Векторы 1) если существует такие с1,с2 ….сn, из которых хотя бы одно не равно нулю, что линейная комбинация равна нулю. 2) если хотя бы один вектор из этой системы можно выразить в виде линейной комбинации остальных. Векторы 1) если линейная комбинация равно нулю тогда и только тогда, когда с1=с2=…=сn=0. 2) если ни один из этих векторов нельзя представить в виде линейных комбинаций остальных. Три ненулевых вектора называют компланарными, если они лежат в одной или параллельных плоскостях. Базис на плоскости и в пространстве Совокупность любых двух линейнонезависимых векторов, принадлежащих данной плоскости, называется базисом этой плоскости.
NB! Любой вектор, лежащий в этой плоскости, можно выразить через эти два вектора.
Совокупность любых трех линейнонезависимых векторов, называется базисом пространства.
Базис в пространстве, векторы которого попарно-перпендикулярны, и длины которых равны единице, называются ортонормированным.
Тройка векторов называется правой, если при наблюдении с конца вектора Тройка векторов называется левой, если при наблюдении с конца вектора
Декартов базис. Длина вектора в декартовом базисе
ДСК: · ортонормированный базис; · тройка ·
Скалярное произведение. Выражение скалярного произведения через координаты. Физический смысл скалярного произведения Скалярным произведением ( NB!
Свойства скалярного произведения: · · · · · Теорема: для того, чтобы два ненулевых вектора были ортогональны (перпендикулярны), необходимо и достаточно, чтобы их скалярное произведение было равно нулю.
Выражение скалярного произведения через координаты
Механический смысл
Механическая работа.
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 778; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.188.166 (0.011 с.) |

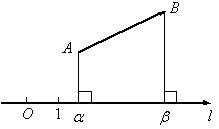 Проекцией вектора, лежащего на оси, на эту ось называется число, по модулю равное длине вектора и взятое со знаком «+», если направление вектора совпадает с направление оси, и со знаком «-», если они противоположны.
Проекцией вектора, лежащего на оси, на эту ось называется число, по модулю равное длине вектора и взятое со знаком «+», если направление вектора совпадает с направление оси, и со знаком «-», если они противоположны. не лежит на оси, тогда из точек А и В опускаются перпендикуляры на ось: получаются точки
не лежит на оси, тогда из точек А и В опускаются перпендикуляры на ось: получаются точки  . Вектор
. Вектор  называется компонентой вектора
называется компонентой вектора  Проекцией вектора, не лежащего на оси, на эту ось называется проекция его компоненты на эту ось.
Проекцией вектора, не лежащего на оси, на эту ось называется проекция его компоненты на эту ось. – проекция вектора
– проекция вектора 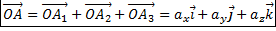 – разложение вектора на компоненты по координатным осям.
– разложение вектора на компоненты по координатным осям. - длина вектора, выраженная через его координаты.
- длина вектора, выраженная через его координаты. .
.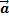 и осью L называется наименьший угол между направлением
и осью L называется наименьший угол между направлением  и положительным направлением оси L.
и положительным направлением оси L.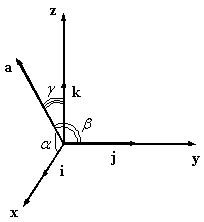 пр L
пр L 





 и n-постоянных с1,с2 ….сn.
и n-постоянных с1,с2 ….сn. - линейная комбинация.
- линейная комбинация. – базис плоскости
– базис плоскости – базис пространства.
– базис пространства.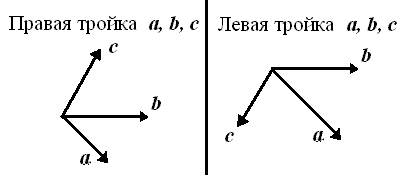
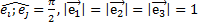
 кратчайший поворот от
кратчайший поворот от  происходит против часовой стрелки.
происходит против часовой стрелки.
 Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат. – правая;
– правая; – координаты вектора
– координаты вектора называется число, равное произведению длин этих векторов на косинус угла между ними.
называется число, равное произведению длин этих векторов на косинус угла между ними.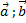 ) - обозначение
) - обозначение .
.