
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы работы с векторными величинамиСодержание книги
Поиск на нашем сайте 1. ГЕОМЕТРИЧЕСКОЕ СЛОЖЕНИЕ ВЕКТОРОВ. а) Правило параллелограмма: вектора б) Правило треугольника: от конца вектора
Для вычисления модуля результирующего вектора необходимо использовать соотношения в треугольниках. 2. НАХОЖДЕНИЕ ПРОЕКЦИЙ ВЕКТОРОВ НА ОСИ КООРДИНАТ. Чтобы найти проекцию вектора Аналогично находятся проекции на другие оси. Проекция вектора на ось - скалярная величина, поэтому математические действия с проекциями производятся алгебраически. Если при перемещении от начала проекции к ее концу движутся по направлению оси, то проекция вектора на эту ось положительна, в противном случае отрицательна. Если вектор перпендикулярен оси, то его проекция на эту ось равна нулю. Если вектор параллелен оси, то модуль проекции равен длине вектора. Если вектор Из рисунка видно, что

СООТНОШЕНИЯ В ПРЯМОУГОЛЬНОМ И ПРОИЗВОЛЬНОМ ТРЕУГОЛЬНИКАХ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
СИНУСОМ острого угла sin КОСИНУСОМ острого угла cos ТАНГЕНСОМ острого угла tg КОТАНГЕНСОМ острого угла ctg ТЕОРЕМА ПИФАГОРА с2= ПРОИЗВОЛЬНЫЙ ТРЕУГОЛЬНИК
Стороны треугольника пропорциональны синусам противолежащих углов.
ТЕОРЕМА КОСИНУСОВ: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
НЕКОТОРЫЕ ФУНКЦИИ И ИХ ГРАФИКИ 1. ЛИНЕЙНАЯ ФУНКЦИЯ
2. ПРЯМАЯ ПРОПОРЦИОНАЛЬНОСТЬ - частный вид линейной функции. При График-прямая, проходящая через начало координат.

Прямо пропорциональная зависимость величин. Две величины 3. ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ Обратно пропорциональная зависимость величин. Две величины 4. КВАДРАТИЧНАЯ ФУНКЦИЯ
ПЛОЩАДИ ГЕОМЕТРИЧЕСКИХ ФИГУР
ТРЕУГОЛЬНИК S= ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК S= ТРАПЕЦИЯ S= КРУГ S= ПОВЕРХНОСТЬ ШАРА S= БОКОВАЯ ПОВЕРХНОСТЬ ЦИЛИНДРА S=
ОБЪЕМЫ ГЕОМЕТРИЧЕСКИХ ТЕЛ
ШАР V=
CВОЙСТВА СТЕПЕНИ
ЗАПИСЬ ЧИСЛА В СТАНДАРТНОМ ВИДЕ
При вычислениях часто получаются числа, которые либо много больше, либо много меньше единицы. Такие числа записывают в стандартном виде: в виде произведения некоторого числа на число десять в соответствующей степени Например: 0,000 025=2,5∙10-5 33 000 000=3,3∙107
РЕШЕНИЕ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ УРАВНЕНИЕ ВИДА: Поделим на множитель при УРАВНЕНИЕ ВИДА: Воспользуемся свойством пропорции: Поделим на множитель при
УРАВНЕНИЕ ВИДА: Представим в виде пропорции: Воспользуемся свойством пропорции: Поделим на множитель при
ПРОИЗВОДНАЯ
Если физическая величина А изменяется с течением времени, то скорость изменения этой величины за промежуток времени Если необходимо определить мгновенную скорость изменения величины, то ищут производную Например: Скорость движения - скорость изменения координаты. Ускорение - скорость изменения скорости. ЭДС индукции - скорость изменения магнитного потока. Мгновенное значение ЭДС индукции = Сила тока I= ИНТЕГРАЛ Операция нахождения производной называется дифференцированием. Обратная дифференцированию задача – интегрирование. Поэтому Геометрический смысл определенного интеграла заключается в том, что это есть площадь криволинейной трапеции, ограниченной графиком функции. Определенный интеграл равен численному значению площади криволинейной трапеции, ограниченной графиком функции Пусть задана функция
Содержание
ПРИСТАВКИ И ИХ МНОЖИТЕЛИ ДЛЯ ОБРАЗОВАНИЯ
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

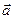 и
и  откладываются от одной точки, результирующий вектор
откладываются от одной точки, результирующий вектор  совпадает с диагональю параллелограмма и начинается в той же точке, от которой откладывались вектора
совпадает с диагональю параллелограмма и начинается в той же точке, от которой откладывались вектора 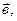 начало результирующего вектора
начало результирующего вектора 
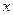 , необходимо на эту ось опустить перпендикуляры из начала и конца вектора. Отрезок
, необходимо на эту ось опустить перпендикуляры из начала и конца вектора. Отрезок  на оси между этими перпендикулярами и будет проекцией вектора
на оси между этими перпендикулярами и будет проекцией вектора 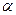 с осью
с осью 


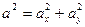 (по теореме Пифагора).
(по теореме Пифагора).





 2+
2+  2 Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.
2 Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.


 рад)
рад)
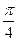 рад)
рад)
 рад)
рад)
 рад)
рад)
 =0,71
=0,71
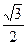 =0,87
=0,87
 , где
, где  . Графиком является прямая, проходящая через точку с координатой
. Графиком является прямая, проходящая через точку с координатой  .
.



 , где
, где  Графиком является гипербола.
Графиком является гипербола. 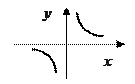
 .
. , где
, где  Графиком является парабола.
Графиком является парабола. (половина произведения основания на высоту).
(половина произведения основания на высоту).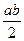 (половина произведения катетов).
(половина произведения катетов). (произведение полусуммы ее оснований на высоту).
(произведение полусуммы ее оснований на высоту).



 ЦИЛИНДР V=
ЦИЛИНДР V= 
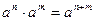






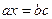

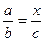
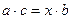
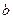 :
: 

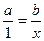


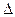 t определяется отношением
t определяется отношением  .
. (t) (определяют отношение
(t) (определяют отношение 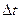 стремящимся к нулю).
стремящимся к нулю). =
= 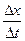 . Мгновенная скорость
. Мгновенная скорость  (t) или
(t) или 
 .
. =
= 
 (t)
(t)

 .
.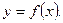 на отрезке
на отрезке  , тогда площадь криволинейной трапеции, ограниченной графиком этой функции вычисляется по формуле
, тогда площадь криволинейной трапеции, ограниченной графиком этой функции вычисляется по формуле 




