
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейно-векторное пространство. Базис. Разложение вектора по базису.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Опр. Линейно-векторное пространство (ЛВП) – это такое множество векторов ЛВП называется n-мерным (обозначается Rn), если в нем максимальное число линейно независимых векторов равно n, а любое множество (n+1) векторов будет линейно зависимым. Поскольку наибольшее число линейно независимых векторов на прямой равно одному, на плоскости - двум, а в пространстве - трем, то размерности этих ЛВП соответственно равны 1, 2 и 3 (обозначение: R1, R2, R3). NB. Множество векторов называется упорядоченным, если каждый из них имеет свой порядковый номер. Система векторов – это всегда упорядоченно е множество векторов. Опр. Базисом в n-мерном ЛВП (Rn) может быть любая система n линейно независимых векторов. Обозначение n-мерного базиса: { Количество базисных векторов всегда равно размерности данного ЛВП. Так как базисные векторы – линейно независимы, то: а) базисом на прямой является любой ненулевой вектор этой прямой; б) базисом на плоскости является любая пара упорядоченных линейно независимых (неколлинеарных) векторов этой плоскости, приведенных к общему началу; в) базисом в пространстве является любая тройка упорядоченных линейно независимых (некомпланарных) векторов, приведенных к общему началу. NB. В любом ЛВП может быть несколько базисов. NB. Любой вектор данного ЛВП можно только единственным образом представить в виде линейной комбинации базисных векторов. Теорема (о разложении вектора по базису на плоскости) На плоскости любой вектор
Запись (1.4) означает, что вектор Доказательство. 1) Пусть (
А
х
Рисунок 1.5
Построенная система координат именуется аффинной системой координат с началом О и базисными векторами 2) Докажем однозначность коэффициентов Теорема (о разложении вектора по базису в пространстве). В пространстве любой вектор
Запись (1.5) означает, что вектор Доказательство. 1) Аналогично случаю на плоскости введем аффинную систему координат в пространстве: { А
z y
A3 A2
x
Рисунок 1.6
Через конец вектора 2) Докажем однозначность коэффициентов Так как по условию векторы
NB 1. Если векторы NB 2. Если векторы Теорема 1. Два вектора Теорема 2. Два вектора
NB. Назначение любого базиса состоит в том, чтобы от линейных операций над векторами перейти к линейным операциям над их координатами.
Основные свойства аффинных координат. 1) При умножении вектора на число его координаты умножаются на это число. Доказательство. Пусть 2) При сложении векторов их соответствующие координаты складываются. Доказательство. Пусть Тогда
Пример 1. В базисе { Решение. Согласно условию Ответ:
Пример 2. В базисе { Решение. Если векторы Так как векторы По теореме Кронекера - Капелли, если число неизвестных n = r(A) = r(A|В), то такая однородная СЛАУ является совместной и определенной, то есть она имеет только тривиальное решение: " NB. Из вида расширенной матрицы следует, что в ее 1-ом столбце записаны координаты вектора
Так как "
и вместо векторов Для данной СЛАУ составим расширенную матрицу и с помощью метода Гаусса приведем ее к ступенчатому виду. NB. Из вида расширенной матрицы следует, что в ее 1-ом столбце записаны координаты вектора
Проекция вектора на ось.
Ось - это прямая с заданным на ней направлением. Положительное направление оси L задается ее ортом Опр. Углом между двумя векторами называется наименьший угол j, на который необходимо повернуть один вектор, чтобы он совпал с другим вектором по направлению. Поворот против хода часовой стрелки считается положительным, а по ходу часовой стрелки - отрицательным (рис.1.7).
а) б) Рисунок 1.7
Очевидно, что 0 £ j < p. NB. Угол между векторами Пусть даны произвольный вектор
B B
A1 B1 B1 A1 aL > 0 aL < 0
а) б) Рисунок 1.8
Опр. Проекция вектора
Основные свойства проекций.
1) Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол и равна нулю, если это
|
||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.67 (0.008 с.) |

 (
( ), для которых определены операции сложения и умножения на действительное число и которые удовлетворяют аксиомам линейности 1 - 7 (п.1.2).
), для которых определены операции сложения и умножения на действительное число и которые удовлетворяют аксиомам линейности 1 - 7 (п.1.2). ;
;  ;…;
;…;  }.
}. можно только единственным образом представить в виде линейной комбинации базисных (неколлинеарных) векторов
можно только единственным образом представить в виде линейной комбинации базисных (неколлинеарных) векторов 

 (1.4)
(1.4) у
у





 А2
А2 О
О  =
=  =
= 

 . Так как по условию векторы
. Так как по условию векторы  Þ
Þ  . Fin.
. Fin. :
:
 (1.5)
(1.5) называются аффинными координатами (компонентами) вектора
называются аффинными координатами (компонентами) вектора 
 O
O =
= 
 Þ
Þ  . Fin.
. Fin. ,
,  ,
,  .
. = (
= ( Þ
Þ 
 =(1; 2; 0);
=(1; 2; 0);  =(-1; 1; 1);
=(-1; 1; 1);  =(2; 0; 1), а в базисе {
=(2; 0; 1), а в базисе {  =(-1; 2; 1). Найти координаты вектора
=(-1; 2; 1). Найти координаты вектора  = 0 возможно лишь тогда, когда
= 0 возможно лишь тогда, когда  = 0. Найдем все возможные значения
= 0. Найдем все возможные значения  . Подставим в данную линейную комбинацию вместо векторов
. Подставим в данную линейную комбинацию вместо векторов  ) их разложение по базису {
) их разложение по базису {  =
= 
 ). В этом случае векторы
). В этом случае векторы 






 ~
~  ~
~  ~
~  -2 ~
-2 ~  ~ ~
~ ~  Þ
Þ  Þ
Þ  =
=  =
=  = 0.
= 0. = 0 (
= 0 ( ;
;  ;
; 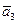 } - базис. Теперь в этом базисе найдем координаты вектора
} - базис. Теперь в этом базисе найдем координаты вектора 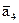 . Для этого запишем формальное разложение вектора
. Для этого запишем формальное разложение вектора  по базису {
по базису { 









 ~
~  ~
~  -2 ~
-2 ~  ~
~  Þ Þ
Þ Þ  Þ
Þ  Þ
Þ  .
.
 L2 L2
L2 L2



 j j
j j


 L1 L1
L1 L1
 .
. и ось L.
и ось L.







 A A
A A
 j j
j j




 L L
L L , где точки А1 и В1 - это основания перпендикуляров, опущенных из начала А и конца В вектора
, где точки А1 и В1 - это основания перпендикуляров, опущенных из начала А и конца В вектора 


