Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешанное произведение векторовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определение 1. Смешанным произведением векторов Свойства смешанного произведения: 1) Смешанное произведение трех векторов равно нулю, если: а) хотя бы один из перемножаемых векторов равен нулю; б) два из перемножаемых векторов коллинеарны; в) все три вектора параллельны одной и той же плоскости (компланарны). 2) Смешанное произведение не изменится, если в нем поменять местами знаки векторного
В силу этого свойства смешанное произведение векторов 3) Смешанное произведение не изменится, если переставить перемножаемые векторы в круговом порядке:
4) При перестановке любых двух векторов смешанное произведение меняет только знак:
Пусть векторы заданы их разложениями по ортам:
Тогда
Из свойства смешанного произведения трех векторов вытекает следующее: необходимым и достаточным условием компланарности трех векторов служит условие Геометрический смысл смешанного произведения трех векторов
Объем пирамиды, построенной на векторах
Пример 1. Показать, что векторы Решение. Находим смешанное произведение векторов:
Так как Пример 2. Найти объем треугольной пирамиды с вершинами Решение. Найдем координаты векторов
Находим смешанное произведение этих векторов:
Так как объем пирамиды равен
Разложение вектора по базису Определение 1. Линейно зависимыми называют векторы
Определение 2. Линейно независимыми называют векторы В системе векторов Пример 1. Определить линейную зависимость (независимость) системы векторов Решение. Сначала рассмотрим систему векторов
Определитель этой матрицы
поэтому Теперь рассмотрим систему векторов
Эта матрица размера Определение 3. Базисом п -мерного пространства Произвольный вектор
Числа Пример 2. Доказать, что векторы
образуют базис в Решение. Каждый из заданных векторов
имеет определитель Вектор
Векторы равны, когда равны их соответствующие координаты. Поэтому из последнего равенства получим:
Матричным методом можно найти решение этой системы
Итак, разложение
Упражнения к разделу 2.1 1. Найти Ответ: 13. 2. Определить угол между векторами Ответ: 3. Найти векторное произведение векторов Ответ: 4. Вычислить площадь параллелограмма, построенного на векторах Ответ: 49. 5. Вычислить площадь параллелограмма, построенного на векторах Ответ: 4. 6. Найти смешанное произведение векторов Ответ: 33. 7. Показать, что векторы 8. Найти скалярное произведение векторов Ответ: –96. 9. Определить угол между векторами Ответ: 10. Вычислить скалярное произведение векторов, заданных своими координатами:
Ответ: 1) 5. 2) 3. 5) 0. 11. Найти внутренние углы треугольника с вершинами Ответ: 12. Определить, при каком значении Ответ: 13. Вычислить работу, произведенную силой Ответ: 16. 14. Вычислить работу, произведенную силой Ответ: 23. 15. Три силы Ответ: 4. 16. Вычислить площадь треугольника с вершинами: 1. 2. 3. 17. Найти объем треугольной пирамиды с вершинами: 1. 2. 3. 18. Сила Ответ: 19. Сила Ответ: 20. Написать разложение вектора
Ответ. 1) 21. Вычислить площадь параллелограмма, построенного на векторах
Ответ. 1)
Аналитическая геометрия
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1097; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 ,
, 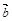 и
и  на вектор
на вектор 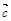 , т.е.
, т.е.  .
. и скалярного
и скалярного 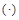 произведения, т.е.
произведения, т.е.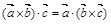 .
. .
. .
.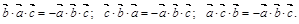
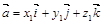 ;
; 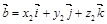 ;
; 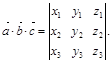 (1)
(1)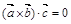 .
.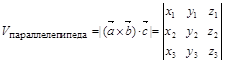 , (2)
, (2)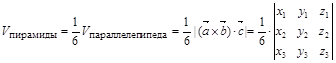 . (3)
. (3) ,
, 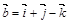 ,
, 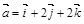 компланарны.
компланарны. .
.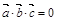 , то заданные векторы компланарны.
, то заданные векторы компланарны.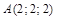 ,
,  ,
, 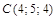 и
и 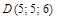 .
.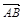 ,
, 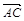 и
и  :
: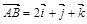 ,
, 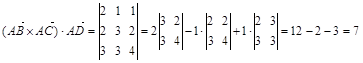 .
. части объема параллелепи-педа, построенного на векторах
части объема параллелепи-педа, построенного на векторах  (куб. ед.).
(куб. ед.).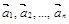 , если существует хотя бы одно действительное число
, если существует хотя бы одно действительное число  , которое не равняется нулю и выполняется равенство
, которое не равняется нулю и выполняется равенство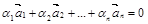 . (1)
. (1)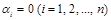 .
.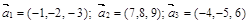 и системы векторов
и системы векторов  .
.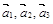 . Найдем ранг матрицы, составленной из координат этих векторов:
. Найдем ранг матрицы, составленной из координат этих векторов: .
.
 ,
,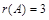 и векторы
и векторы 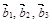 . Матрица В составлена из координат этих векторов и имеет вид:
. Матрица В составлена из координат этих векторов и имеет вид: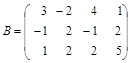 .
.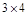 имеет ранг
имеет ранг 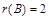 , поэтому векторы
, поэтому векторы  называют любую совокупность п линейно независимых векторов п -мерного пространства.
называют любую совокупность п линейно независимых векторов п -мерного пространства.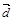 п -мерного пространства можно представить в виде линейной комбинации векторов базиса
п -мерного пространства можно представить в виде линейной комбинации векторов базиса 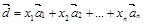 . (2)
. (2) называются координатами вектора
называются координатами вектора 
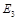 , и разложить вектор
, и разложить вектор  в этом базисе.
в этом базисе.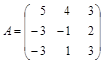 ,
,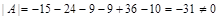 , поэтому векторы
, поэтому векторы  .
. .
. .
. .
. , если
, если  .
.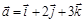 и
и  .
.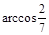 .
.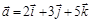 и
и 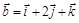 .
.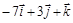 .
.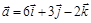 и
и 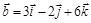 .
. и
и  , если
, если 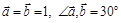 .
.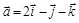 ,
,  ,
, 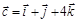 .
.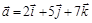 ,
, 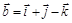 ,
,  компланарны.
компланарны.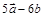 , если
, если 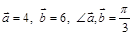 .
. и
и 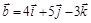 .
.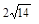 .
.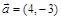 ;
;
 .
.
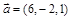 ;
;
 .
.
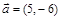 ;
;
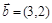 .
.
 ;
;
 .
.
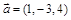 ;
;
 .
.
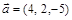 ;
;
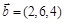 .
.
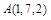 ,
, 
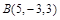 ,
, 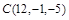 .
.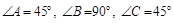 .
. векторы
векторы  и
и  перпендикулярны.
перпендикулярны. .
. при перемещении ее точки приложения с начала в конец вектора
при перемещении ее точки приложения с начала в конец вектора 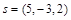 .
. при прямолинейном перемещении ее точки приложения из точки
при прямолинейном перемещении ее точки приложения из точки 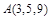 в точку
в точку 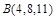 .
.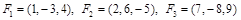 , которые приложены в одной точке. Вычислить, какую работу делает равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения
, которые приложены в одной точке. Вычислить, какую работу делает равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения 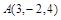 в положение
в положение 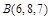 .
.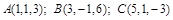 . Ответ: 14.
. Ответ: 14. . Ответ:
. Ответ: 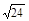 .
. . Ответ:
. Ответ: 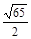 .
.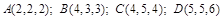 . Ответ:
. Ответ:  .
.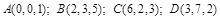 . Ответ: 20.
. Ответ: 20.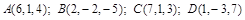 . Ответ:
. Ответ:  .
.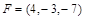 приложена к точке
приложена к точке 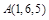 . Найти момент этой силы относительно начала координат.
. Найти момент этой силы относительно начала координат.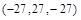 .
. приложена к точке
приложена к точке  . Найти момент этой силы относительно точки
. Найти момент этой силы относительно точки 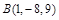 .
.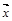 по векторам
по векторам  ,
, 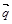 и
и  .
.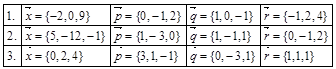
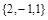 . 2)
. 2) 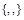 . 3)
. 3)  .
.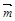 и
и 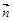 (
( – угол между векторами
– угол между векторами 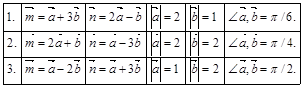
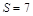 2)
2) 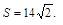 3)
3)