
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешенное произведение векторов его св-ва и вычисления.Содержание книги
Поиск на нашем сайте
Смешанным произведением векторов
Свойствасмешанного произведения: 1)Смешанное произведение равно нулю, если: а)хоть один из векторов равен нулю;б)два из векторов коллинеарны;в)векторы компланарны. 2) 4) Для нахождения длины высоты пирамиды найдем сначала площадь основания CD. Sосн =
Линейной зависимость векторов Вектор а1,а2,…аn наз-ся линейнозависимым, если сущ. Числа l1, l2,… ln не все равные нулю, для к-х справедливо равенство: l1а1+lа2+…lnаn=0. Если векторы линейнозависимы, то один из них можно представить виде линейной комбинации остальных. Справедливо и обратное утверждение. Векторы а1,а2,…аn наз-ся линейнонезавис., если l1а1+lа2+…lnаn=0. Имеет место только при условии l1=l2=…=ln=0. Теорема: Всякие 3 вектора а,b и с на пл. ленейнозависимы Следствие: если число векторов на пл. больше 3-х, то они всегда линейнозависимы Теорема: 2 вектора на пл. линейноз.Û когда они неколлинеарны. Теорема: всякие 4 вектора а,b,с и d в простр. линейнозависимы. Следствие: 1. если число данных веторов в простр. больше 4-х, то они линейноз. 2. для того, чтобы 3 вектора в простр. были компланарны, необх. И дост., чтобы они были линейноз. и наоборот. 3. для того, чтобы 3 вектора были линейно независимы необх. и дост., чтобы они были компланарны Базис на пл. и в простр. Аффинные координаты Базис - совокупн. линейнонезавис. векторов Базис на плоскости – два любые неколлинеарные вектора, взятые в определенном порядке.
Базис в пространстве – три любые некомпланарных вектора, взятые в определенном порядке. Пусть произв. Вектора a,b и c на пл. образуют базисÞ a= l1b+l2c (1) Это выражение называют разложением вектора а по базису b и c, а числа l1,l2 наз-ся аффинными координатами вектора а и запис-ся: а={l1,l2}=(l1,l2) и такое разложение явл-ся единтсвенным. Аналогично, любой вектор а в пространстве однозначно разлагается по векторам b,c и d. а= l1b+l2c + l3d, а= (l1,l2,l3). Прямоугольный декартов Базис
Т.к. они не компланарны, то они образуют базис, к-й называется декартовым. Если известны декартовы координаты векторов, то линейные операции над векторами можно заменить арифм. действ. над их проекциями. Если даны координаты точек А(х1,y1,z1) и B(x2,y2,z2, то проекции вектора прox AB=x2-x1; прoy AB=y2-y1; прoz AB=z2-z1,т.е. разложение вектора АВ по Базису: АВ=(x2-x1)i +(y2-y1)j + (z2-z1)k ½AB½=Ö(x2-x1)2 +(y2-y1)2 + (z2-z1)2
24. Направляющие косинусы вектора а – косинусы углов между вектором и осями координат и равны отношению прилегающего катета к гипотенузе, т.е. отношению координат вектора к его модулю. Пусть вектор а разложен по Базису след обр.: а= axi+ayj+azk ax =½a½*cosa; ay =½a½*cosb; az =½a½*cosc Þ cosa= ax /½a½ cosb= ay /½a½ cosc= az /½a½, т.к
19.Полярные координаты. Пусть на плоскости дана точка О – полюс и луч ОР – полярная ось. Тогда положение точки М на плоскости определяет полярный угол j = ÐМОР и радиус-вектор r = ОМ. Пару (r,j)-называют полярными координатами,где r-полярный радиус точки, j-полярный угол. Если полярная ось совпадает с осями координат декарт сист., то х = r Cos j, y = Sin j и обратный переход r = Öx2 + y2, tg j = y / x.
|
|||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 342; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.240 (0.01 с.) |

 ,
,  и
и  называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора  на вектор, равный векторному произведению векторов
на вектор, равный векторному произведению векторов  и
и  .Обозначается
.Обозначается  или (
или ( ). Смешанное произведение
). Смешанное произведение  по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах  ,
,  и
и 




 3)
3) 
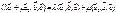 5) Объем треугольной пирамиды, образованной векторами
5) Объем треугольной пирамиды, образованной векторами  ,
,  и
и  , равен
, равен  6)Если
6)Если  ,
, 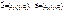 , то
, то  Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.Найдем координаты векторов:
Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.Найдем координаты векторов:  Найдем смешанное произведение полученных векторов:
Найдем смешанное произведение полученных векторов:  ,Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).Найдем координаты векторов:
,Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).Найдем координаты векторов:  Объем пирамиды
Объем пирамиды 


 (ед2)Т.к. V =
(ед2)Т.к. V =  ; (ед)
; (ед) 
 ½a½=Öax2+ay2+az2 имеем cosa= ax/Öax2+ay2+az2 и т.д.
½a½=Öax2+ay2+az2 имеем cosa= ax/Öax2+ay2+az2 и т.д.


