
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система линейных уравнений. Определение решения линейной системы. Исследование линейной системы 2-х уравн. С 2-мя неизв.Содержание книги
Поиск на нашем сайте Система линейных уравнений. Определение решения линейной системы. Исследование линейной системы 2-х уравн. С 2-мя неизв. Рассмотрим сист. 2-х уравн. С 2-мя неизв. ì ía11x1+a12x2=b1 î a21x1+a22x2=b2 Введем обозначение: D=½a11 a12½ ½a21 a22½ Dx1=½b1 a12½ ½b2 a22½
Dx2=½a11 b1½ ½ a21 b2½ D-это определитель, составленный из коэффициентов, стоящих перед неизв. Определители Dx1 и Dx2 составл.из опред. D заменой столбца коэффициентов при соотв. перем. На столбец своб. Членов b1 и b2. Для нахождения неизв. x1 и x2 необх. Воспольз. Формулой: x1=Dx1/D; x2=Dx2/D. Итак, если D отличен от нуля, то система имеет единственное решение, опред. По данным фомулам, если D=0, то сист. Может иметь множ. Реш. Или их совсем не иметь.
Система m уравнений с n неизвестными в общем виде записывается следующим образом: где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.
Определитель квадратной матрицы 2-го порядка. Формулы Крамера. Любые 4 числа, расположенные в виде квадратной таблицы, называются квадратной матрицей второго порядка. Каждой квадратной матрице 2-ого порядка можно поставить в соответствие число, называемое её определителем и обозначаемое D=|A|. Определитель матр. 2-го порядка равен числу a11· a22-a21·a12 Св-ва опред. 2-го порядка: 1. опред. Не измен. Если его строки поменять местами с соотв. столбцами 2. при перестановки 2-х строк(или столбцов) опред. Изменит знак на противоп. 3. опред. С двумя одинак. Строками или столб. Равен нулю 4. общий множит. Всех элем. Строки или столбца можно выносить за знак опред. 5. если все элем. Какой-л. строки(ст.) равны нулю, то опред. Равен нулю 6. если к элем. К-л. строки или столб. Опред. Приб. В соотв. элем. Др. строки или ст., умножен. На одно и то же число, то опред не изм. 7. опред. Равен алгебр. Сумме произв. Элем. К.-л. строки (ст) на их алгебр. Доп. Теорема Крамера Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.Для этого необходимо, чтобы определитель матрицы системы не равнялся 0. Система из n уравнений с n неизвестными
Если система однородна, т.е. bi = 0, то при D¹0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.При D = 0 система имеет бесконечное множество решений. Определитель 3-го порядка. Алгебраические дополнения, теорема о разложении определителя третьего порядка. 9 элементов aij, где i-номер строка, а j-номер столбца, располагаются в квадратную таблицу, называемую квадратной матрицей третьего порядка. Ей можно поставить в соответствие число, которое называется определителем 3-го порядка. Опред. Равен алгебр. Сумме произв. Элем. К.-л. строки (ст.) на их алгебр. Доп. Алгебраическое дополнение Aij для элемента aij – число равное (-1) i+jMij, где Mij минор элемента aij. Минор Mij элемента Aij матрицы А наз-ся определитель, полученный из исходного определителя А вычеркиванием итой строки и житого столбца.
Первый замечательный предел
В силу четности входящих в неравенство ф-ий, докажем это неравенство на промежутке
2. следовательно, что
1. Покажем, что
2. Докажем, что
3. Последнее утверждение:
Основные теоремы о пределах Теорема 1. Теорема 2. Теорема 3. Следствие. Теорема 4. Теорема 5. Если f(x)>0 вблизи точки х = а и Теорема 6. Если g(x) £ f(x) £ u(x) вблизи точки х = а и Функция f(x) называется ограниченной вблизи точки х = а, если существует такое число М>0, что ïf(x)ï<M вблизи точки х = а. Теорема 7. Если функция f(x) имеет конечный предел при х®а, то она ограничена вблизи точки х = а. Доказательство. Пусть
Второй замечательный предел это форма второго замечательного предела, справедлива и для действ. аргумента lim(n®¥)(1+1/n)n=e Основная теорема алгебры Всякий многочлен с любыми числовыми коэф., степень к-го не меньше единицы имеет хотя бы один корень в общем случае комплексный. Рассмотри многочлен ¦(х) с комплексн. коэф., как комплексн. функцию комплексного переменного. Таким обр. х может принимать любые значения, т.е. переменная х ихменяется на комплексной плоскости. Значение функции ¦(х) также будут комплексными числами. Можно считать, что эти значения отличаются на второй комплексной плоскости, подобно тому, как в случае действит. Функций действ. Переменного. Значения независимого переменного отмечаются на одн. Числ. Прямой(оси абсцисс), а значение функции на др.(оси ординат). Замечание: многочлен ¦(х) является непрерывной функцией комлексного переменного х для любого положит. Числа e,можно найти токое положит. Число d, что из усл. |х-х0| ád Þ |¦(х) -¦(х0) | á e. Лемма: если своб. Член многочлена ¦(х) = a0xn+ a1xn-1 + a2xn-2+…+ an-1x равен нулю т.е. r(o)=0, то для всякого e ñ 0 можно подобрать такое dñ0,что при всех х, для к-х |х| ád будет |¦(х) | áe Действительно, пусть число а имеет макс. значение: А=max (|a0|, |a1|,|a2|,…|an-1|). Число e нам уже дано. Покажем, что если число d взять равным выражением d = e/А+e, то оно будет удовлетворять требуемым усл. В самом деле, |¦(х) |£ |a0||х|n+|a1||х|n-1 +…+ |an-1||х| £ А(|х|n+|х|n-1+|х|), т.е. ¦(х) £ А |х|- |х|n+1|/1- |х|, т.к. |х| ád и d =e/А+e, получим: |х|-|х|n+1/1- |х| á |х|/ 1- |х|, т.е. ¦(х) á А |х||/1- |х | á А*d/1-d á А* (e/А+e)/ 1- (e /А+e)=e. ЧТД (12-14).(1) Прямоугольные координаты на плоскости Две взаимно перпендикулярные оси Ox и Oy, имеющие общее начало O и одинаковую единицу масштаба, образуют декартову (или прямоугольную) систему координат на плоскости. Ось Ox называется осью абсцисс, ось Oy - осью ординат, точка O - началом координат. Плоскость, в которой расположены оси Ox и Oy, называется координатной плоскостью и обозначается Oxy. Пусть M - произвольная точка плоскости. Опустим из неё перпендикуляры MA и MB на оси Ox и Oy. Прямоугольными координатами x и y точки M называются величины OA и OB направленных отрезков OA иOB: x=OA, y=OB. Координаты x и y точки M называются соответственно её абсциссой и ординатой. Символ M(x;y) означает, что точка M имеет координаты x и y. Начало координат имеет координаты (0;0). Таким образом, каждой точке плоскости соответствует пара чисел (x;y) - её прямоугольные координаты. Оси координат разбивают плоскость на четыре части, их называют четвертями, квадрантами или координатными углами и нумеруют римскими цифрами I, II, III, IY.
Предел функции в точке Пусть функция f(x) определена в некоторой проколотой окрестности точки x0. Число A называется пределом функции f(x) при x → x0 (или в точке x0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < |x − x0| < δ, справедливо неравенство |f(x) − A| < ε, т.е. lim x → x0 f(x) = A ε > 0 δ > 0: 0 < |x − x0| < δ |f(x) − A| < ε. Используем понятие окрестности и учтем, что 0 < |x − x0| < δ x • O δ (x0) и |f(x) − A| < ε f(x) Oε (A). (Точка над символом окрестности указывает, что это проколотая окрестность.) Теперь определение предела функции в точке можно представить в виде lim x → x0 f(x) = A ε > 0 δ > 0: x • Oδ (x0) f(x) Oε (A).
10. Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью.
Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:
Сопряжённые комплексные числа имеют одинаковый модуль. __ Аргумент комплексного числа - это угол Тригонометрическая форма комплексного числа. Абсциссу a и ординату b комплексного числа a + bi можно выразить через его модуль r и аргумент
УРАВНЕНИЯ ПРЯМОЙ. 1) Прямая может быть задана уравнениями двух плоскостей
2). пересекающихся по этой прямой. Исключив поочередно x и y из уравнений, получим
3). Здесь прямая определена двумя плоскостями, проецирующими её на плоскости x0Z и y0Z. Уравнения прямой, проходящей через две точки M1(x1;y1;z1) и M2(x2;y2;z2) имеют вид
18. Угол между плоскостями, расстояние от точки до плоскости. Расстояние от точки до плоскости. Это длина перпендикуляра, опущенного из данной точки на данную плоскость.
В
АВ перпендикулярны плоскости альфа; длина перпендикуляра АВ- расстояние от точки А до плоскости альфа.
Угол альфа0 угол между плоскостями альфа и бэтта.
Система линейных уравнений. Определение решения линейной системы. Исследование линейной системы 2-х уравн. С 2-мя неизв. Рассмотрим сист. 2-х уравн. С 2-мя неизв. ì ía11x1+a12x2=b1 î a21x1+a22x2=b2 Введем обозначение: D=½a11 a12½ ½a21 a22½ Dx1=½b1 a12½ ½b2 a22½
Dx2=½a11 b1½ ½ a21 b2½ D-это определитель, составленный из коэффициентов, стоящих перед неизв. Определители Dx1 и Dx2 составл.из опред. D заменой столбца коэффициентов при соотв. перем. На столбец своб. Членов b1 и b2. Для нахождения неизв. x1 и x2 необх. Воспольз. Формулой: x1=Dx1/D; x2=Dx2/D. Итак, если D отличен от нуля, то система имеет единственное решение, опред. По данным фомулам, если D=0, то сист. Может иметь множ. Реш. Или их совсем не иметь.
Система m уравнений с n неизвестными в общем виде записывается следующим образом: где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.
|
||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

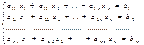
 в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:xi = Di/D, где D = опред. Матр., а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:xi = Di/D, где D = опред. Матр., а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов Доказательство: докажем для
Доказательство: докажем для  справедливость неравенства
справедливость неравенства 
 Из рисунка видно, что площадь кругового сектора
Из рисунка видно, что площадь кругового сектора
 , так как х >0, то
, так как х >0, то  ,
,








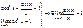
 , где С = const.Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.
, где С = const.Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а. Доказательство этой теоремы будет приведено ниже.
Доказательство этой теоремы будет приведено ниже.

 при
при 
 , то А>0. Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.
, то А>0. Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0. , то и
, то и  .
. , т.е.
, т.е.  , тогда
, тогда или
или  ,.е.
,.е.  где М = e + ïАïТеорема доказана.
где М = e + ïАïТеорема доказана.





 между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan
между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan 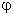 :
:



 А
А




 Угол между двумя плоскостями это наименьший двугранный угол, получившийся при пересечении этих плоскостей. Угол между 2 плоскостями может принимать значение от 0* до 90*. Если угол между плоскостями=0, то эти плоскости совпадают или переллельны. Если угол между плоскостями =90*, то плоскости перпендикулярны.
Угол между двумя плоскостями это наименьший двугранный угол, получившийся при пересечении этих плоскостей. Угол между 2 плоскостями может принимать значение от 0* до 90*. Если угол между плоскостями=0, то эти плоскости совпадают или переллельны. Если угол между плоскостями =90*, то плоскости перпендикулярны.


