
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые последовательности и пределыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если каждому натуральному числу n поставлено в соответствие некоторое вещественное число Существует несколько способов задания числовых последовательностей. Последовательность может быть задана при помощи формулы, позволяющей вычислить каждый ее член по номеру (например, Часто последовательность задается при помощи рекуррентной формулы, позволяющей определить каждый член последовательности по одному или нескольким предыдущим; при этом необходимо задание одного или нескольких первых членов последовательности. К таковым относятся арифметическая и геометрическая прогрессии или, например, последовательность Фибоначчи, задаваемая формулой
и условиями x1 = 1, x2 = 1. Иногда последовательность задается описанием ее членов, например, последовательность, у которой xn равен n-му знаку после запятой в десятичной записи числа π = 3,14159265358979323..., задается следующим образом: x1 = 1, x2 = 4, x3 = 1, x4 = 5, x5 = 9, x6 = 2, x7 = 6, x8 = 5, x9 = 3, x10 = 5 и т. д. Число a называется пределом последовательности {xn}, если для каждого ε > 0 существует такой номер Nε, что для всех n ≥ Nε выполняется неравенство
т. е.
Интервал (a – ε; a + ε) называют ε-окрестностью точки a. Проще говоря, число a называется пределом последовательности {xn}, если в любой ε-окрестности точки a лежат все члены последовательности {xn}, за исключением, может быть, конечного их числа. Отсюда легко заметить, что изменение конечного числа членов последовательности не влияет ни на факт существования предела, ни на величину последнего. Так, если Для стабилизирующейся последовательности (т. е. последовательности {xn} такой, что xn = a при n ≥ n0) в качестве Nε для любого ε можно взять n0. Последовательность, у которой существует предел, называется сходящейся. Если никакое число не является пределом последовательности, то она называется расходящейся. Можно показать, что числовая последовательность имеет только один предел. Последовательность
Последовательность
Если в этих определениях неравенство будет нестрогим, то последовательности будут называться соответственно неубывающей и невозрастающей. Возрастающие и убывающие последовательности называют строго монотонными. Неубывающие и невозрастающие последовательности называют монотонными.
Элементы аналитической геометрии в пространстве. Уравнение плоскости. Пусть
УРАВНЕНИЯ ПРЯМОЙ. 1) Прямая может быть задана уравнениями двух плоскостей
2). пересекающихся по этой прямой. Исключив поочередно x и y из уравнений, получим
3). Здесь прямая определена двумя плоскостями, проецирующими её на плоскости x0Z и y0Z. Уравнения прямой, проходящей через две точки M1(x1;y1;z1) и M2(x2;y2;z2) имеют вид
18. Угол между плоскостями, расстояние от точки до плоскости. Расстояние от точки до плоскости. Это длина перпендикуляра, опущенного из данной точки на данную плоскость.
В
АВ перпендикулярны плоскости альфа; длина перпендикуляра АВ- расстояние от точки А до плоскости альфа.
Угол альфа0 угол между плоскостями альфа и бэтта.
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.138 (0.006 с.) |

 то говорят, что задана числовая последовательность
то говорят, что задана числовая последовательность  Кратко она обозначается символом
Кратко она обозначается символом 
 называют n -м членом последовательности. Совокупность этих чисел называют множеством значений последовательности.
называют n -м членом последовательности. Совокупность этих чисел называют множеством значений последовательности. ).
). При этом пишут, что
При этом пишут, что  или
или  при n → ∞. Кратко это определение можно записать так:
при n → ∞. Кратко это определение можно записать так:
 то
то  Действительно, выбрав для произвольного ε > 0
Действительно, выбрав для произвольного ε > 0 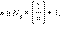 получаем
получаем  , так как
, так как  . Здесь существенно, что Nε зависит от ε.
. Здесь существенно, что Nε зависит от ε. называется возрастающей, если для любого
называется возрастающей, если для любого  выполняется неравенство
выполняется неравенство называется убывающей, если для любого
называется убывающей, если для любого  выполняется неравенство
выполняется неравенство - радиус-вектор текущей точки M(x,y) плоскости;
- радиус-вектор текущей точки M(x,y) плоскости;  - единичный вектор, имеющий направление перпендикуляра, опущенного на плоскость из начала координат;
- единичный вектор, имеющий направление перпендикуляра, опущенного на плоскость из начала координат;  - углы, образованные этим перпендикуляром с осями координат Ox, Oy, Oz; p - длина этого перпендикуляра, тогда уравнение плоскости в векторной форме имеет вид
- углы, образованные этим перпендикуляром с осями координат Ox, Oy, Oz; p - длина этого перпендикуляра, тогда уравнение плоскости в векторной форме имеет вид
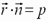 При переходе к координатам уравнение принимает вид:
При переходе к координатам уравнение принимает вид:


 А
А




 Угол между двумя плоскостями это наименьший двугранный угол, получившийся при пересечении этих плоскостей. Угол между 2 плоскостями может принимать значение от 0* до 90*. Если угол между плоскостями=0, то эти плоскости совпадают или переллельны. Если угол между плоскостями =90*, то плоскости перпендикулярны.
Угол между двумя плоскостями это наименьший двугранный угол, получившийся при пересечении этих плоскостей. Угол между 2 плоскостями может принимать значение от 0* до 90*. Если угол между плоскостями=0, то эти плоскости совпадают или переллельны. Если угол между плоскостями =90*, то плоскости перпендикулярны.


