
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства сходящихся последовательностейСодержание книги
Поиск на нашем сайте
Министерство труда, занятости и социальной защиты РТ Государственное автономное образовательное учреждение среднего профессионального образования «Колледж малого бизнеса и предпринимательства»
Методические указания по математике для заочного отделения специальности 260807 «Технология продукции общественного питания»
Разработала: преподаватель Корнеева Наталья Сергеевна
Казань 2012 Содержание
1) Чтение учебника 2) Решение задач 3) Самопроверка.
1) Последовательности 2) Функция, предел функции 3) Производные и дифференциалы 4) Численное интегрирование
Введение В настоящее время математические методы широко используются для решения самых разнообразных задач науки, техники и экономики. Значение этих методов существенно выросло в связи с массовым применением во всех отраслях электронно- вычислительных машин. Математика является фундаментальной дисциплиной. Цель ее преподавания в учреждении среднего профессионального образования предусматривает: - развить логическое мышление и повысить общий уровень математической культуры; - познакомить студентов с математическим аппаратом. Необходимым для изучения общенаучных дисциплин; - выработать у студентов умение самостоятельно изучать учебную литературу по математике и ее приложениям; - выработать навыки к математическому исследованию прикладных задач.
Общие рекомендации студенту-заочнику по работе над курсом математики
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебнику, решение задач. Самопроверка. Выполнение контрольных работ. Во время сессий студенты слушают лекции, посещают практические занятия. Сдают устные зачеты и экзамены. При самостоятельном изучении учебного материала можно использовать следующие рекомендации.
Чтение учебника 1. Каждый следующий вопрос должен изучаться только после правильного понимания предыдущего. 2. Особое внимание следует обращать на определение основных понятий. Их следует знать точно, а также подробно разбирать примеры, которые поясняют такие определения и уметь строить аналогичные примеры самостоятельно. 3. При изучении материала по учебнику полезно вести конспект, в который рекомендуется вписывать определения, формулировки теорем, уравнения и т.д. На полях конспекта необходимо отмечать вопросы, на которые необходимо получение устной или письменной консультации преподавателя. 4. Выводы, полученные в виде формул, рекомендуется подчеркивать или обводить рамкой, чтобы при перечитывании они выделялись и лучше запоминались. Полезно составить лист, содержащий важнейшие и наиболее часто употребляемые формулы курса. Такой лист поможет запомнить эти формулы, а также послужит постоянным справочником.
Решение задач
Самопроверка При изучении математики большое значение имеет проверка правильности понимания, усвоения и выполнения задания. Необходимо научиться самопроверке. При этом приемы самоконтроля могут быть различные: - проверка правильности усвоения материала путем сравнения своих формулировок с данными в учебнике (если свои записаны); - проверка результатов решения задачи по готовому ответу, а еще лучше по готовому решению, когда сразу видно, в каких местах есть пробелы; - проверка результатов решения по аналогичному решению; - проверка результата с помощью обратных действий.
Требования к выполнению и оформлению письменной контрольной работы
При выполнении контрольной работы необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
Теория к контрольной работе Последовательности Пусть задан занумерованный бесконечный набор чисел х1,х2,…,хn,…. Это значит, что всякому натуральному числу n=1,2,… поставлено в соответствие по определенному закону число хn. Определение: Всякий занумерованный бесконечный набор чисел х1,х2,…,хn,… называется числовой последовательностью. Пример: 1) Последовательность всех четных натуральных чисел 2,4,6,….2n,… 2) Последовательность всех квадратов натуральных чисел 1,4,9,16,…n2,… Обозначают: хn, n=1,2,… или Хn называется общим членом последовательности.
Способы задания последовательностей
Пример: хn=
Пример: х1=х2=1, хn=xn-1+xn-2
Пример: последовательность простых чисел 2,3,5,7,11,13,17,19,23,… (т.е. можно указать саму последовательность, но для нее нет общего члена) Определение: последовательность Определение: Числовая последовательность Определение: Числовая последовательность Определение: Неограниченная последовательность, для которой неравенство Пример: Определение: числовая последовательность называется бесконечно малой(б.м.), если
Предел последовательности Рассмотрим последовательность хn=
Определение: Число А называется пределом последовательности хn, n=1,2…, если разность αn=хn-А является б.м. последовательностью. Обозначается предел символом Замечание: предел постоянной равен самой постоянной. Последовательности, имеющие предел, называются сходящимися; в противном случае последовательность называется расходящейся. Теорема 1: Если последовательность имеет предел, то он единственный. Заметим, что из определения можно сделать вывод, что б.м. последовательности – это те и только те, предел которых равен нулю, т.е. сказать, что хn,n=1,2… - б.м. и Функция. Предел функции. Пусть Х и У – некоторые множества и каждому элементу х х – аргумент функции Х – область определения У- область значений. Если Х и У-множество действительных чисел, то говорят о числовой функции. примерами числовых функций являются линейная (у=ах+b), тригонометрическая (у=cos x),… Функции могут быть заданы с помощью формул, таблиц, словесно и т.д. Рассмотрим поведение функции при условии, что х стремится к числу а (х Определение: число b называется пределом функции у=f(x) при х Обозначается: Пример: Основные теоремы о функциях, имеющих предел, аналогичны теоремам для сходящихся последовательностей. неопределенности и способы их раскрытия для функций определяются аналогично последовательностям. Таблица замечательных пределов
Пример: Найти предел
При решении использовалось свойство для вычисления предела суммы двух функций и первый замечательный предел.
Бесконечно малые функции. Метод эквивалентных бесконечно малых величин. Определение: Функция α(х) называется бесконечно малой при х Бесконечно малые функции могут стремиться к нулю по-разному или. как говорят, с разной скоростью. Поэтому их принято сравнивать между собой в зависимости от того, как ведет себя их отношение. Пусть α(х) и β(х) – две бесконечно малые (б.м.) функции при х Определение: Б.м. α(х) и β(х) называют б.м. одного порядка малости, если существует предел Пример: Получаем, что б.м. функции х2 и 1-cosx имеют один порядок малости. Определение: Две б.м. функции α(х) и β(х) называются эквивалентными при х Примерами эквивалентных б.м. функций являются пары функций, приводящие к замечательным пределам (см.таблицу). Эквивалентность б.м. обозначается символом ~
Таблица эквивалентных величин (при х
Практическое значение таблицы определяется следующей теоремой Теорема: Пустьα(х) ~ α1(х), β(х) ~ β1(х) и существует Пример: Найти предел Т.к. sin2x~2х при х
Непрерывность функции
Пусть функция у=f(х) определена в некоторой окрестности точки а, включая саму точку а. Определение: Функция у=f(х) называется непрерывной в точке а, если: 1) она определена в точке а; 2) существует 3) Если хотя бы одно из условий не выполняется, то говорят, что функция у=f(x) имеет разрыв в точке а, а сама точка а называется точкой разрыва. Обозначим х-х0 = Утверждение: Все элементарные функции непрерывны в каждой точке своей области определения. Правила дифференцирования 1. 2. 3. 4.
Таблица производных элементарных функций 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Здесь а= const, u-u(x)/если u(x)=x, то Правило Лопиталя – Бернулли применяется для раскрытия неопределенностей
Если после применения правила Лопиталя неопределенность сохраняется, то правило следует применить еще раз. Пример: Варианты контрольной работы 1-13. Вычислите указанные пределы. 1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) 11. а) 12. а) 13. а) 14-26. Найти производную 1. а) y=arctg 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) 11. а) 12. а) 13. а) 27-39. Найти наибольшее и наименьшее значение функции y=f(x) на отрезке 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Список литературы Основная литература 1.Григорьев С.Г., Задулина С.В. Математика. - М.: Издательский центр «Академия», 2005.-384с. 2.Григорьев В.П. Элементы высшей математики. - М.: Издательский центр «Академия»,2004.
Дополнительная литература 1. Виленкин Н.Я., Шварцбурд С.И. Математический анализ.- М., «Просвещение»,1973. 2. Данко П.Е. и др. Высшая математика в упражнениях и задачах.Ч.1,2.-М.:Высш.школа,1999. Министерство труда, занятости и социальной защиты РТ Государственное автономное образовательное учреждение среднего профессионального образования «Колледж малого бизнеса и предпринимательства»
Методические указания по математике для заочного отделения специальности 260807 «Технология продукции общественного питания»
Разработала: преподаватель Корнеева Наталья Сергеевна
Казань 2012 Содержание
1) Чтение учебника 2) Решение задач 3) Самопроверка.
1) Последовательности 2) Функция, предел функции 3) Производные и дифференциалы 4) Численное интегрирование
Введение В настоящее время математические методы широко используются для решения самых разнообразных задач науки, техники и экономики. Значение этих методов существенно выросло в связи с массовым применением во всех отраслях электронно- вычислительных машин. Математика является фундаментальной дисциплиной. Цель ее преподавания в учреждении среднего профессионального образования предусматривает: - развить логическое мышление и повысить общий уровень математической культуры; - познакомить студентов с математическим аппаратом. Необходимым для изучения общенаучных дисциплин; - выработать у студентов умение самостоятельно изучать учебную литературу по математике и ее приложениям; - выработать навыки к математическому исследованию прикладных задач.
Общие рекомендации студенту-заочнику по работе над курсом математики
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебнику, решение задач. Самопроверка. Выполнение контрольных работ. Во время сессий студенты слушают лекции, посещают практические занятия. Сдают устные зачеты и экзамены. При самостоятельном изучении учебного материала можно использовать следующие рекомендации.
Чтение учебника 1. Каждый следующий вопрос должен изучаться только после правильного понимания предыдущего. 2. Особое внимание следует обращать на определение основных понятий. Их следует знать точно, а также подробно разбирать примеры, которые поясняют такие определения и уметь строить аналогичные примеры самостоятельно. 3. При изучении материала по учебнику полезно вести конспект, в который рекомендуется вписывать определения, формулировки теорем, уравнения и т.д. На полях конспекта необходимо отмечать вопросы, на которые необходимо получение устной или письменной консультации преподавателя. 4. Выводы, полученные в виде формул, рекомендуется подчеркивать или обводить рамкой, чтобы при перечитывании они выделялись и лучше запоминались. Полезно составить лист, содержащий важнейшие и наиболее часто употребляемые формулы курса. Такой лист поможет запомнить эти формулы, а также послужит постоянным справочником.
Решение задач
Самопроверка При изучении математики большое значение имеет проверка правильности понимания, усвоения и выполнения задания. Необходимо научиться самопроверке. При этом приемы самоконтроля могут быть различные: - проверка правильности усвоения материала путем сравнения своих формулировок с данными в учебнике (если свои записаны); - проверка результатов решения задачи по готовому ответу, а еще лучше по готовому решению, когда сразу видно, в каких местах есть пробелы; - проверка результатов решения по аналогичному решению; - проверка результата с помощью обратных действий.
Требования к выполнению и оформлению письменной контрольной работы
При выполнении контрольной работы необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
Теория к контрольной работе Последовательности Пусть задан занумерованный бесконечный набор чисел х1,х2,…,хn,…. Это значит, что всякому натуральному числу n=1,2,… поставлено в соответствие по определенному закону число хn. Определение: Всякий занумерованный бесконечный набор чисел х1,х2,…,хn,… называется числовой последовательностью. Пример: 1) Последовательность всех четных натуральных чисел 2,4,6,….2n,… 2) Последовательность всех квадратов натуральных чисел 1,4,9,16,…n2,… Обозначают: хn, n=1,2,… или Хn называется общим членом последовательности.
Способы задания последовательностей
Пример: хn=
Пример: х1=х2=1, хn=xn-1+xn-2
Пример: последовательность простых чисел 2,3,5,7,11,13,17,19,23,… (т.е. можно указать саму последовательность, но для нее нет общего члена) Определение: последовательность Определение: Числовая последовательность Определение: Числовая последовательность Определение: Неограниченная последовательность, для которой неравенство Пример: Определение: числовая последовательность называется бесконечно малой(б.м.), если
Предел последовательности Рассмотрим последовательность хn=
Определение: Число А называется пределом последовательности хn, n=1,2…, если разность αn=хn-А является б.м. последовательностью. Обозначается предел символом Замечание: предел постоянной равен самой постоянной. Последовательности, имеющие предел, называются сходящимися; в противном случае последовательность называется расходящейся. Теорема 1: Если последовательность имеет предел, то он единственный. Заметим, что из определения можно сделать вывод, что б.м. последовательности – это те и только те, предел которых равен нулю, т.е. сказать, что хn,n=1,2… - б.м. и Свойства сходящихся последовательностей Теорема 2:Пусть хn и уn,n=1,2,… - сходящиеся последовательности, т.е. lim xn=a, limyn=b. Тогда справедливы следующие утверждения: 1) для любого числа М последовательность Мхn тоже сходится, причем 2) сумма (разность) хn и уn также сходится, причем 3) произведение хnynтакже сходится, причем 4) при условии, что b пример:Най
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.226 (0.016 с.) |


 , n=1,2,…
, n=1,2,… .
. .
.

 , n=1,2,…
, n=1,2,… …,т.е. члены этой последовательности с увеличением номера приближаются к нулю. Если рассмотреть другую последовательность, то там может быть другое число, к которому приближаются члены последовательности.
…,т.е. члены этой последовательности с увеличением номера приближаются к нулю. Если рассмотреть другую последовательность, то там может быть другое число, к которому приближаются члены последовательности.
 - одно и то же.
- одно и то же. Х поставлено в соответствие по некоторому правилу у
Х поставлено в соответствие по некоторому правилу у  а)
а) а), сходящейся к а, соответствующая последовательность значений функции у(х1), у(х2),…у(хn),… сходится к b.
а), сходящейся к а, соответствующая последовательность значений функции у(х1), у(х2),…у(хn),… сходится к b.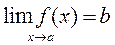


 первый замечательный
предел
первый замечательный
предел



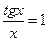
 , где α-вещественный
параметр
, где α-вещественный
параметр



 -второй
замечательный предел
-второй
замечательный предел



 =0+
=0+  =2
=2  =2
=2 , если она имеет предел, причем этот предел равен нулю, т.е.
, если она имеет предел, причем этот предел равен нулю, т.е. 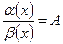 , причем А
, причем А 
 .
. R
R
 . Тогда существует и предел
. Тогда существует и предел 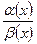 , причем
, причем  =
=  =0+2=2
=0+2=2
 .
. у-у0=
у-у0=  у. тогда определение непрерывности можно сформулировать по-другому: функция называется непрерывной а точке х, если из условия
у. тогда определение непрерывности можно сформулировать по-другому: функция называется непрерывной а точке х, если из условия 
 следует, что и
следует, что и 



 В частности
В частности  ;
; 










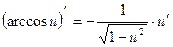


 .
. при вычислении пределов функции:
при вычислении пределов функции: , т.е. если функции дифференцируемы, то предел отношения функций равен пределу отношения их производных.
, т.е. если функции дифференцируемы, то предел отношения функций равен пределу отношения их производных. В этом примере правило Лопиталя использовали три раза.
В этом примере правило Лопиталя использовали три раза. б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
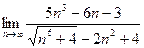 б)
б) 
 б)
б) 
 б)
б) 
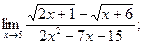 б)
б) 
 ; б)
; б) 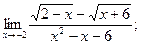
 данных функций.
данных функций. ;
; ;
;


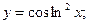

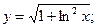

 ;
;


 .
. на отрезке
на отрезке 
 на отрезке
на отрезке 
 на отрезке
на отрезке  на отрезке
на отрезке 
 на отрезке
на отрезке 
 на отрезке
на отрезке 
 на отрезке
на отрезке 
 на отрезке
на отрезке 
 на отрезке
на отрезке  на отрезке
на отрезке  на отрезке
на отрезке  (Mxn)=M
(Mxn)=M  yn)=a
yn)=a  =
= 



