
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства непрерывных функций ⇐ ПредыдущаяСтр 3 из 3
Пусть функции f(x) и y(x) непрерывны в точке а, с-любое число. Тогда функции сf(x), f(x)±y(x), f(x)·y(x), Свойства непрерывных функций отражают 2 теоремы. Известные как теоремы Вейерштрасса. Определение: Функция у=f(х), определенная на отрезке Первая теорема Вейерштрасса: Если функция f(x) непрерывна на отрезке Определение: Значение f(x0), где х0 Максимальное значение функции в точке обозначают Аналогично определяется минимальное значение функции в точке. Вторая теорема Вейерштрасса: Если функция f(x) непрерывна на отрезке
Дифференциальное исчисление функции одной переменной Разность х-х0 называется приращением аргумента и обозначается Приращением функции у=f(х) в точке х0 называется разность Если существует предел отношения Производную функции можно обозначать символами: у/, Операция нахождения производной функции называется дифференцированием функции. Из равенства С геометрической точки зрения производная – это угловой коэффициент касательной к графику функции в данной точке. С физической точки зрения производная – это скорость изменения функции по отношению к изменению аргумента. Определение: Если у=f(u) есть функция аргумента u, u=u(x) есть функция аргумента х, то y=f(u(x)) есть сложная функция от х. Производная сложной функции вычисляется по формуле
Правила дифференцирования 1. 2. 3. 4.
Таблица производных элементарных функций 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Здесь а= const, u-u(x)/если u(x)=x, то Правило Лопиталя – Бернулли применяется для раскрытия неопределенностей
Если после применения правила Лопиталя неопределенность сохраняется, то правило следует применить еще раз. Пример:
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.112.69 (0.005 с.) |
 (y(x)≠0) также непрерывны.
(y(x)≠0) также непрерывны. , называется ограниченной на этом отрезке, если найдется число М>0 такое, что для любого х
, называется ограниченной на этом отрезке, если найдется число М>0 такое, что для любого х  выполняется неравенство
выполняется неравенство  .
. , а саму точку – хmax
, а саму точку – хmax т.е.
т.е.  =х-х0, тогда близкая к х0 точка х=х0+
=х-х0, тогда близкая к х0 точка х=х0+  .
. у=f(х0+
у=f(х0+  ,
,  .
.
 dy – дифференциал функции.
dy – дифференциал функции.




 В частности
В частности  ;
; 










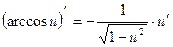


 .
. при вычислении пределов функции:
при вычислении пределов функции: , т.е. если функции дифференцируемы, то предел отношения функций равен пределу отношения их производных.
, т.е. если функции дифференцируемы, то предел отношения функций равен пределу отношения их производных. В этом примере правило Лопиталя использовали три раза.
В этом примере правило Лопиталя использовали три раза.


